| M. Michel CABANE | Président |
| M. Pierre DROSSART | Rapporteur |
| M. Ray PIERREHUMBERT | Rapporteur |
| M. Patrick MASCART | Rapporteur |
| M. Alain HAUCHECORNE | Examinateur |
| M. Daniel GAUTIER | Examinateur |
| M. Olivier TALAGRAND | Examinateur |
Travaux réalisés :
au Laboratoire de Météorologie Dynamique du CNRS
Institut Pierre Simon Laplace
NOLOGO
Un grand merci d'abord aux étudiants que j'ai eu le plaisir d'encadrer ces dernières années et qui ont contribué à des titres divers à l'avancée des travaux présentés ici. Plutôt que de les nommer dans ce préambule, je les ai mentionnés au fil des chapitres. Beaucoup de ces étudiants ont depuis trouvé leur place, dans la recherche ou ailleurs, mais quelques uns sont venus malheureusement grossir durablement les bataillons de la précarité que nous avons laissé prospérer autour de nos instituts de recherche.
Merci ensuite aux collègues qui gravitent autour du noyau dur du "LMD-Jussieu" et avec qui nous avons construit au fil des ans un environnement de travail sérieux et néanmoins fort sympathique sans lequel ce travail n'aurait pas été possible. Quand je pense à cet environnement, me vient souvent l'image d'une niche écologique où compétences (depuis la physique fondamentale jusqu'au secrétariat), intelligence et originalité s'additionnent dans la bonne humeur, à l'abri du carriérisme et de la surenchère programmatique et technocratique qui semblent le lot quotidien de la recherche "moderne" ; où l'on sait encore qu'avant d'aller jouer les moulins à vent de mitinges en projets européens, il faut avoir du grain à moudre et donc commencer par labourer, semer, moissonner. Alors, à vous tous qui vous reconnaîtrez, un immense merci.
Je veux enfin remercier ceux des responsables qui m'ont épaulé à un moment ou un autre au cours de ces travaux. Comme ils auront peut-être plus de difficulté à se reconnaître, je citerai en particulier Olivier Talagrand, Jean-Paul Huot, Gérard Mégie, Sylvie Joussaume, Hervé Le Treut et Claude Basdevant. Merci enfin aux voyageurs, proches ou lointains, qui ont accepté de participer au jury.
Deux objectifs, en partie contradictoires, m'ont guidé dans la rédaction de ce document. Le premier est d'ordre statutaire : pour soutenir une Habilitation à Diriger des Recherches, il faut rédiger une synthèse de ses travaux antérieurs, souvent déjà publiés en anglais dans des revues à comité de lecture. Le second objectif que je me suis fixé est de profiter de cet exercice imposé pour essayer d'écrire un texte qui puisse servir plus ou moins directement de support de travail pour des collègues, voir de support pédagogique sur différents sujets auxquels je me suis intéressé au cours des dix dernières années. Faute d'avoir pu y consacrer suffisamment de temps, ces objectifs ne sont certainement que partiellement atteints. Les rapporteurs et examinateurs ne manqueront pas de trouver le document trop long. Les collègues ou étudiants voulant se renseigner sur un des sujets abordés le trouveront incomplet ou elliptique ; déséquilibré entre des parties trop techniques et d'autres trop vagues. J'espère que l'exercice restera malgré tout utile. Parmi les efforts pour accroître la lisibilité, j'ai essayé de réduire au maximum le nombre des acronymes utilisés et de répertorier en fin de document ceux qui sont utilisés.
Le texte est composé de quatre parties plus ou moins indépendantes, avec à chaque fois une introduction assez complète et des conclusions et perspectives. L'introduction et la conclusion du document sont donc plutôt là pour brosser le cadre général du travail pour l'une et tracer des perspectives générales pour l'autre. Le fil conducteur de ces différentes parties est le transport atmosphérique et la modélisation de ce transport dans les modèles globaux de climat.
Les couplages entre composition et transport atmosphérique occupent une place grandissante dans l'étude des atmosphères planétaires.
Ces couplages sont tout d'abord au centre d'une partie des questions
relatives au changement climatique.
En effet,
une part des incertitudes
relatives au réchauffement global du climat terrestre provient
des incertitudes sur l'évolution de la
composition même de l'atmosphère (CO![]() , méthane, ozone troposphérique,
aérosols).
Or l'évolution de cette composition est étroitement liée au
transport atmosphérique et au climat.
Pour le CO
, méthane, ozone troposphérique,
aérosols).
Or l'évolution de cette composition est étroitement liée au
transport atmosphérique et au climat.
Pour le CO![]() , l'augmentation des concentrations atmosphériques
sous l'effet des émissions anthropiques conduit à une augmentation
du stockage dans les océans et les écosystèmes.
Le puits biosphérique est lui-même sensible à l'évolution
du climat. Les estimations actuelles prévoient une réduction du
puits biosphérique consécutive au changement climatique qui
pourrait correspondre
à une rétroaction positive de 15
, l'augmentation des concentrations atmosphériques
sous l'effet des émissions anthropiques conduit à une augmentation
du stockage dans les océans et les écosystèmes.
Le puits biosphérique est lui-même sensible à l'évolution
du climat. Les estimations actuelles prévoient une réduction du
puits biosphérique consécutive au changement climatique qui
pourrait correspondre
à une rétroaction positive de 15![]() sur la teneur en CO
sur la teneur en CO![]() de l'atmosphère
(Dufresne, 2002).
La modification de l'ozone troposphérique est également étroitement
couplée à l'évolution de la température et de l'humidité.
Les changements des vents en surface peuvent également modifier le soulèvement
des poussières désertiques
ou les émissions de DMS (précurseurs des aérosols soufrés)
par les océans (Bopp et al., 2004).
de l'atmosphère
(Dufresne, 2002).
La modification de l'ozone troposphérique est également étroitement
couplée à l'évolution de la température et de l'humidité.
Les changements des vents en surface peuvent également modifier le soulèvement
des poussières désertiques
ou les émissions de DMS (précurseurs des aérosols soufrés)
par les océans (Bopp et al., 2004).
Au-delà des modifications de la composition, la sensibilité du climat à un changement de concentration imposé est également souvent conditionnée par des processus de transport. La fameuse rétroaction vapeur d'eau (l'atmosphère plus chaude se charge en vapeur d'eau, ce qui augmente en retour l'effet de serre) peut par exemple être fortement modulée par les processus de transport. Si on suppose par exemple que le réchauffement résulte également en une augmentation de l'altitude de la pénétration de la convection (convection nuageuse ou grands systèmes de Hadley-Walker), l'air subsident autour de ces zones convectives sera au contraire plus sec. Même si les processus de transport sont plus complexes (cf. par exemple Pierrehumbert, 1998), il n'en reste pas moins que l'accroissement d'humidité lors d'un réchauffement climatique peut être modulé par les changements d'advection. Les effets indirects des aérosols (une augmentation du nombre de noyaux de condensation résultant en des nuages formés de plus petites gouttes, donc plus brillants et moins précipitants) sont également une source importante d'incertitude sur l'amplitude du changement climatique, étroitement liée au transport et à la microphysique.
Concernant les couplages entre composition et dynamique atmosphérique sur les
autres planètes, on mentionnera d'abord le cas des poussières sur Mars.
En dehors des bandes d'absorption du CO![]() , constituant majoritaire
de la fine atmosphère martienne, la poussière est le principal constituant
actif radiativement. Cette poussière est en permanence soulevée du sol du
grand désert martien
par des rafales de vent, des tornades ou de petites tempêtes locales.
Régulièrement, des tempêtes
plus importantes se déclenchent, soulevant la poussière sur des milliers
de kilomètres. A certaines périodes de l'année, ces tempêtes peuvent
finalement dégénérer en évènements globaux spectaculaires, au cours desquels
la surface de Mars est entièrement voilée pour l'
, constituant majoritaire
de la fine atmosphère martienne, la poussière est le principal constituant
actif radiativement. Cette poussière est en permanence soulevée du sol du
grand désert martien
par des rafales de vent, des tornades ou de petites tempêtes locales.
Régulièrement, des tempêtes
plus importantes se déclenchent, soulevant la poussière sur des milliers
de kilomètres. A certaines périodes de l'année, ces tempêtes peuvent
finalement dégénérer en évènements globaux spectaculaires, au cours desquels
la surface de Mars est entièrement voilée pour l'![]() il
d'un observateur extérieur. La circulation est alors profondément modifiée
(Hourdin et al., 1993).
Notons enfin les
couplages entre la photochimie, la microphysique des brumes et la
circulation stratosphérique sur Titan qui ont largement retenu notre attention
au cours des années passées et qui font l'objet d'un chapitre du présent
document.
il
d'un observateur extérieur. La circulation est alors profondément modifiée
(Hourdin et al., 1993).
Notons enfin les
couplages entre la photochimie, la microphysique des brumes et la
circulation stratosphérique sur Titan qui ont largement retenu notre attention
au cours des années passées et qui font l'objet d'un chapitre du présent
document.
La modélisation numérique globale est devenue un outil de base pour aborder ces systèmes complexes. Les modèles de circulation générale atmosphérique, développés au début des années 70 pour les besoins de la prévision météorologique, se sont petit à petit enrichis tant sur le plan physique (représentation des nuages, modèles thermodynamiques du sol, paramétrisation de la convection) que par la prise en compte du couplage avec les autres composantes du système climatique. On pense en particulier pour la Terre au couplage avec l'océan, la végétation, la chimie ou les aérosols. Ces développements ont abouti dans les années récentes au concept de ``modèles intégrés du climat" (les soi-disant ``Earth system models") utilisés notamment pour essayer de prévoir les évolutions futures du climat. Un modèle de ce type est actuellement développé et utilisé à l'IPSL. Il comprend, couplé au modèle de circulation générale atmosphérique LMDZ, le modèle de circulation générale océanique ORCALIM, le modèle des surfaces continentales ORCHIDEE et le module aérosols-chimie INCA. Ce modèle est actuellement impliqué dans la réalisation de ``scénarios climatiques" pour le prochain rapport du GIEC.
Une des originalités de la recherche menée au LMD est d'étudier
de front et avec le même outil, LMDZ, le climat de la Terre et celui
d'autres planètes du système solaire, en particulier Mars
et Titan.
En parallèle du développement du modèle intégré terrestre, et souvent
même avant, les versions planétaires ont connu des évolutions similaires.
Sur Mars, ce sont les couplages avec le cycle du
carbone (un quart de l'atmosphère de CO![]() se condense saisonnièrement
dans les calottes polaires), des poussières (on en a parlé plus haut)
et de l'eau (avec l'enjeu de déterminer les réservoirs d'eau sous la surface
et de comprendre les évolutions passées du climat de la planète rouge) qui
ont été inclus dans les modèles de circulation existants
(Forget et al., 1998; Montmessin, 2004; Hourdin et al., 1995a,1993).
Pour Titan, les couplages avec la photochimie et la brume
(Lebonnois et al., 2003b; Rannou et al., 2002; Hourdin, 2004) ou le méthane (Tokano, 2001) ont
également été inclus dans les modèles existants.
se condense saisonnièrement
dans les calottes polaires), des poussières (on en a parlé plus haut)
et de l'eau (avec l'enjeu de déterminer les réservoirs d'eau sous la surface
et de comprendre les évolutions passées du climat de la planète rouge) qui
ont été inclus dans les modèles de circulation existants
(Forget et al., 1998; Montmessin, 2004; Hourdin et al., 1995a,1993).
Pour Titan, les couplages avec la photochimie et la brume
(Lebonnois et al., 2003b; Rannou et al., 2002; Hourdin, 2004) ou le méthane (Tokano, 2001) ont
également été inclus dans les modèles existants.
Pour la modélisation des couplages entre composition et climat,
une étape essentielle du travail de développement
consiste à introduire, dans le modèle de circulation générale atmosphérique,
les algorithmes permettant de représenter le transport des espèces traces.
Il faut traiter à la fois le transport par l'écoulement explicitement représenté
dans le modèle de circulation (c'est à dire pour des échelles supérieures
à quelques centaines ou dizaines de kilomètres) et le transport
par les écoulements non résolus, turbulents ou convectifs.
C'est en fait l'introduction, dans le modèle LMDZ,
de schémas permettant de représenter le transport à grande échelle
qui a donné le coup d'envoi à l'ensemble des études présentées ici.
Nous avons plus particulièrement mis en ![]() uvre dans le modèle LMDZ
des schémas en volumes finis développés
à l'origine par Van Leer (1977).
Les versions terrestre et planétaires étant développées de front,
ce travail d'introduction du transport a été effectué de fait
à la fois pour la Terre, Mars et Titan.
Cette version avec transport des traceurs du modèle LMDZ est à l'origine d'un
grand nombre de développements et applications concernant ces trois planètes.
Ce travail préliminaire est décrit dans le Chapitre 2.
uvre dans le modèle LMDZ
des schémas en volumes finis développés
à l'origine par Van Leer (1977).
Les versions terrestre et planétaires étant développées de front,
ce travail d'introduction du transport a été effectué de fait
à la fois pour la Terre, Mars et Titan.
Cette version avec transport des traceurs du modèle LMDZ est à l'origine d'un
grand nombre de développements et applications concernant ces trois planètes.
Ce travail préliminaire est décrit dans le Chapitre 2.
Je me suis ensuite plus particulièrement intéressé au transport vertical par les structures méso-échelles de la couche limite convective. Ces structures (rouleaux, cellules thermiques), bien connues des amateurs de vol libre (deltaplanes, planeurs, parapentes), ne sont en général pas considérées de façon spécifique dans les modèles de circulation globaux, qui privilégient, à un bout, une vision en diffusion du transport turbulent dans la couche limite et, à l'autre bout, des schémas de convection profonde, contrôlés pour une bonne part par les changements de phase de l'eau. Les modèles doivent du coup inclure des traitements adhoc (``contre-gradients", ``ajustement convectif") pour pallier l'absence de paramétrisation des structures convectives de couche limite ; ces structures convectives qui, sur des régions désertiques ou sur une planète-désert comme Mars, peuvent dominer le transport vertical jusqu'à plusieurs kilomètres au-dessus de la surface. Cette nouvelle paramétrisation, le ``modèle du thermique", basée sur une formulation dite ``en flux de masse", est décrite en détail dans le Chapitre 3. Y sont également présentées différentes validations par rapport à des simulations numériques des grands tourbillons ou à des observations.
En marge des questions relevant directement des couplages entre composition et climat, les outils développés pour le transport des espèces traces peuvent être utilisés pour étudier la dispersion de polluants atmosphériques à écoulement atmosphérique connu. On présente dans les chapitres 2 et 3 de tels calculs de dispersion, réalisés ici à des fins de validation des algorithmes de transport. Dans ces simulations numériques, on force le modèle de circulation atmosphérique à suivre au plus près la situation synoptique afin de comparer, au jour le jour, les concentrations observées de certains constituants avec des données de terrain. La technique employée est baptisée ``nudging" en Anglais ce qu'on traduira ici par ``guidage". Cette technique consiste à relaxer en permanence les champs météorologiques du modèle vers des données d'``analyses" ou ``réanalyses" produites par les grands centres de prévisions météorologiques. Dans ce cas, le modèle de circulation joue le rôle d'une espèce d'interpolateur physique sur le maillage choisi et permet de recalculer un jeu cohérent de grandeurs physiques nécessaires à la représentation du transport grande échelle et sous-maille. Les grandeurs nécessaires pour les algorithmes de transport des traceurs peuvent être soit passées directement aux algorithmes concernés, soit stockées dans des fichiers puis relues pour le seul calcul du transport des espèces traces. On parlera de modes ``branché" et ``débranché".
Il s'avère que le modèle guidé et débranché, développé à l'origine pour des besoins de validation dans le cadre des études couplées chimie-climat, est un modèle global de dispersion atmosphérique parfaitement adapté à certaines questions relatives à la surveillance de l'environnement. Un travail spécifique a été entrepris dans ce domaine suite à une demande du CEA relative à la surveillance des essais nucléaires à partir de la mesure de la concentration en éléments radioactifs. Il s'agit d'un cas classique de problème inverse dans lequel on veut obtenir des contraintes sur les sources à partir de mesures de concentration. Avec Robert Sadourny, nous nous sommes convaincus, à l'époque de la demande, qu'il était légitime, pour répondre à cette question, d'inverser la direction du temps dans le modèle de transport Eulérien (débranché). En émettant un traceur au niveau des détecteurs, le modèle calcule alors la distribution d'origine de l'air échantillonné à la station.
L'utilisation du transport inverse et de ``modèles de détecteurs" pour aborder ce type de question n'est pas nouvelle. Mais le fait qu'on puisse utiliser directement les codes Eulériens à rebours dans le temps (ce que nous appellerons le ``rétro-transport Eulérien'') ne semblait pas vraiment acquis. Ce travail sur la détection des essais nucléaires a donc été l'occasion de clarifier la théorie sous-jacente. Le rétro-transport Eulérien peut être présenté d'un point de vue physique comme une formulation Eulérienne de l'approche des rétro-trajectoires Lagrangiennes, largement utilisée dans la communauté des chimistes de l'atmosphère pour interpréter des mesures de composition ponctuelles. Le rétro-transport Eulérien peut également être présenté d'un point de vue mathématique comme l'adjoint du transport direct pour un produit scalaire particulier, pondéré par la masse de l'air sous-tendant le transport. Les visions à la base des rétro-trajectoires et de l'approche adjointe sont cependant suffisamment différentes pour que les outils développés le soient aussi, avec des conséquences importantes sur l'efficacité des algorithmes d'inversion. Le Chapitre 4 présente de façon détaillée à la fois les aspects théoriques, des illustrations numériques et des exemples d'application pour la surveillance des essais nucléaires. Les outils développés à cette occasion sont en cours d'intégration dans une chaîne opérationnelle au CEA.
La dernière partie de ce document concerne Titan, le plus gros satellite de Saturne. Titan fait partie de ces objets fascinants du système solaire révélés par l'épopée Voyager. En 1981, les responsables des missions Voyager choisissent de privilégier pour la sonde Voyager 1 un survol de Titan plutôt que de poursuivre la course vers Uranus et Neptune (périple magistralement réussi ensuite par Voyager 2). On sait en effet à l'époque que Titan est, avec la Terre, le seul corps tellurique du système solaire entouré d'une atmosphère dense d'azote (1,5 bar à la surface). Les photos renvoyées vers la Terre sont très décevantes. Une épaisse couche de brume orangée voile entièrement la surface. Tout juste peut-on distinguer un léger contraste entre les deux hémisphères, signe probable d'un effet saisonnier. Les mesures spectroscopiques permettent en revanche d'identifier un grand nombre de composés chimiques, hydrocarbures et nitriles. Ces espèces chimiques, créées dans la très haute atmosphère à partir de la photo-dissociation de l'azote moléculaire et du méthane (second constituant atmosphérique) sont ensuite transportées vers le bas dans la stratosphère où on pense qu'elles polymérisent pour donner naissance à la brume orange. L'analyse des contrastes latitudinaux de température dans la stratosphère suggère également que l'atmosphère tourne beaucoup plus vite que le satellite, lui-même en phase bloquée autour de Saturne, avec une durée du jour de 16 jours terrestres environ. Si la direction de la rotation de l'atmosphère ne peut être obtenue à partir des observations de la température, l'analogie avec Vénus et des arguments théoriques suggèrent que l'atmosphère est en régime de ``superrotation", l'atmosphère vers 200 km tournant une dizaine de fois plus vite que la surface et dans la même direction.
Suite au passage des sondes Voyager, une mission est programmée vers le système de Titan, sous l'impulsion de Toby Owen et Daniel Gautier. La sonde américaine Cassini se consacrera au système de Saturne et emmènera à son bord la sonde européenne Huygens qui plongera dans l'atmosphère de Titan. Mission parfaitement remplie. Le 14 janvier 2005, après 7 années de voyage dans le système solaire, la sonde Huygens a dévoilé sous l'épaisse couche de brume des paysages familiers où chacun reconnaît qui sa Côte d'Azur, qui son lac de montagne ; en tout cas des images qui évoquent un rivage.
Au début des années 90s, sous l'impulsion de Daniel Gautier (LESIA) et Christopher P. McKay (NASA/Ames), différents travaux de modélisation sont entrepris pour interpréter les résultats des missions Voyager et préparer la mission Cassini-Huygens. Le modèle de circulation du LMD est adapté aux conditions de Titan (Hourdin et al., 1995b) et prédit effectivement une forte superrotation sur Titan, superrotation confirmée depuis par des mesures Doppler. En parallèle, des modèles unidimensionnels sont développés pour la photochimie (Toublanc et al., 1995) et la microphysique des brumes (Cabane et al., 1992; Rannou et al., 1995). Il apparaît cependant rapidement que les différentes composantes de ce système sont fortement couplées. Les brumes sont formées par la polymérisation des constituants chimiques et peuvent servir également de noyaux de condensation à ces dernières au niveau de la troposphère glaciale de Titan (70 K environ). Brumes et espèces chimiques sont évidemment transportées par les vents. En retour, les contrastes latitudinaux de la composition jouent les premiers rôles dans le forçage de la circulation. Vers 1995, nous décidons, avec Michel Cabane et Dominique Toublanc, de réunir les différents efforts de modélisation pour s'attaquer à ce système climatique complet.
En 1998, lors du colloque quadriénal du Programme National de Planétologie,
le programme est déjà clair
(Hourdin et al., 1998) :
``L'arrivée sur Titan de la mission Cassini-Huygens est sans doute une des dernières occasions
avant des décennies d'explorer un système physique analogue à la Terre mais encore très mal connu.
Pour l'atmosphère et le climat
en particulier, c'est une occasion unique avant longtemps de mettre à l'épreuve pour
une planète tellurique les théories
et modèles développés dans le contexte terrestre.
Cette perspective ainsi que la préparation de la mission (étude en amont et préparation de
l'analyse des résultats) ont motivé le développement d'un modèle de circulation générale de
l'atmosphère de Titan au Laboratoire de Météorologie Dynamique du CNRS, sous l'impulsion
de Daniel Gautier et en collaboration avec Christopher P. McKay (NASA/Ames) et Régis
Courtin (LESIA/Obs. Paris Meudon).
[...]
Pour Titan, le modèle prédit une stratosphère tournant environ 10 fois plus vite que la planète
solide avec des vents zonaux (d'ouest) de l'ordre de 100 m s![]() .
En plus de ce phénomène dynamique spectaculaire, les résultats du modèle ont contribué à mettre
en évidence l'importance des couplages entre dynamique atmosphérique, microphysique des
aérosols, et photochimie. Ceci nous a conduit à bâtir et à proposer au PNP pour les années
à venir, un projet de modélisation du climat de Titan intégrant ces différentes
composantes. L'enjeu est d'importance et la tâche ardue quand on connaît les problèmes
rencontrés dans la modélisation de ces problèmes sur Terre. Mais la perspective de la
confrontation du modèle aux observations de la mission Cassini-Huygens en 2005
en font [un objectif] scientifique de tout premier plan.''
.
En plus de ce phénomène dynamique spectaculaire, les résultats du modèle ont contribué à mettre
en évidence l'importance des couplages entre dynamique atmosphérique, microphysique des
aérosols, et photochimie. Ceci nous a conduit à bâtir et à proposer au PNP pour les années
à venir, un projet de modélisation du climat de Titan intégrant ces différentes
composantes. L'enjeu est d'importance et la tâche ardue quand on connaît les problèmes
rencontrés dans la modélisation de ces problèmes sur Terre. Mais la perspective de la
confrontation du modèle aux observations de la mission Cassini-Huygens en 2005
en font [un objectif] scientifique de tout premier plan.''
Après une mise en route souvent ardue, le modèle couplé a bien été développé. Il a permis de mettre en évidence le couplage très fort entre la brume et les vents (Rannou, 2004). Le modèle a également permis d'expliquer les contrastes latitudinaux observés dans la composition chimique (Hourdin, 2004; Lebonnois et al., 2001). Sur la base de simulations numériques effectuées avec cet outil, une base de données a été constituée et mise à disposition de la communauté sur la toile avant l'arrivée de la mission (Rannou et al., 2005). Les données sont là. Les premières photos ont réservé leur lot de surprises. Que nous réservent les dépouillements en cours des enregistrements des spectromètres et "imageurs spectraux" ou des mesures in-situ de la composition par Huygens ?
C'est cette histoire qui clôt ce document (Chapitre 5) avant quelques conclusions générales.
Le présent chapitre est consacré à la représentation du transport atmosphérique d'espèces traces dans les modèles de circulation atmosphérique de grande échelle ainsi qu'à la présentation d'un outil particulier : la version ``traceurs" du modèle de circulation générale LMDZ.
Le LMD développe et exploite depuis le début des années 70
un modèle de circulation générale atmosphérique.
Comme beaucoup d'autres, ce modèle s'est petit à petit enrichi pour devenir
un véritable
modèle climatique, avec par exemple la prise en compte des couverts végétaux
pour prédire le comportement thermodynamique des surfaces continentales ou
le couplage avec l'océan.
Le transport d'espèces traces est pour sa part introduit une première
fois par Sylvie Joussaume (1990) dans une version précédente du modèle de climat
du LMD pour étudier le cycle des poussières désertiques.
Christophe Genthon introduit ensuite le Radon (![]() Rn) et le
plomb (
Rn) et le
plomb (![]() Pb) dans le modèle en utilisant, pour représenter l'advection,
le schéma des Pentes du NASA/GISS (Preiss, 1997; Genthon, 1995).
Pb) dans le modèle en utilisant, pour représenter l'advection,
le schéma des Pentes du NASA/GISS (Preiss, 1997; Genthon, 1995).
Au milieu des années 80, Robert Sadourny et Phu LeVan entreprennent la réécriture du noyau hydrodynamique du modèle, afin de le rendre plus modulaire, lisible et efficace (l'ancien modèle avait été écrit sur cartes perforées par Phu LeVan pour des machines ne pouvant pas contenir un champ entier en mémoire) et de généraliser l'idée de grille étirable qui avait été une première fois testée pour étudier un cyclone en baie du Benghal. C'est cette possibilité de raffinement de la grille qui donnera plus tard le "Z" (pour zoom) de LMDZ. Du fait de l'inertie inhérente à la modélisation du climat terrestre (on regarde des choses très précises avec un modèle robuste dont on connaît bien le fonctionnement et dont on a ``réglé" la climatologie), ce nouveau noyau dynamique est dans un premier temps utilisé sur Mars (Hourdin et al., 1995a,1993) et Titan (Hourdin, 1992; Hourdin et al., 1995b). Pour ces deux planètes, un des prolongements possibles des études développées au LMD consistait à s'intéresser au cycle d'espèces transportées : les poussières sur Mars, avec les spectaculaires tempêtes globales qui peuvent voiler la surface de la planète pendant plusieurs dizaines de jours, et les brumes et espèces chimiques sur Titan, dont on montre dans le dernier chapitre de ce document qu'elles sont fortement couplées à la circulation atmosphérique.
Les traceurs sont introduits dans LMDZ en 1996, en utilisant, pour l'advection
de grande échelle, des schémas en volumes finis2.1.
Les schémas en volumes finis sont basés sur une partition du domaine considéré
en volumes de contrôle, aux frontières desquels on évalue les flux entrants
ou sortants de traceurs.
Ce sont des schémas basés sur une formulation intégrale de l'équation
de transport.
Nous avons plus précisément codé et testé une série de schémas en
volumes finis proposés à l'origine par Van Leer (1977).
Ces schémas conduisent facilement à une mise en ![]() uvre tridimensionnelle et
satisfont des propriétés physiques fondamentales du transport: localité,
conservation, monotonie, positivité (plus généralement pas de création
d'extrema numériques) et invariance par addition d'une constante au champ de
traceur.
Van Leer (1977) avait en fait proposé une hiérarchie de schémas dont les plus
sophistiqués ont été introduits ultérieurement et indépendamment dans la
communauté météorologique par Russell et Lerner (1981) (schéma des pentes du NASA/GISS) et
Prather (1986).
Avec Alexandre Armengaud alors en thèse au LGGE sous la direction de Christophe
Genthon, nous avons testé dans LMDZ plusieurs de ces schémas (Hourdin et Armengaud, 1999).
Nous avons pu montrer que leurs performances étaient
en fait assez semblables dès lors qu'on les comparait non pas à résolution
spatiale fixée mais à coût numérique équivalent (un schéma plus précis mais
plus coûteux se comporte comme un schéma moins précis mais utilisé sur une
grille plus fine). Nous avons retenu pour le modèle du LMD le schéma le plus
simple (le schéma I dans l'article original de Van Leer souvent appelé MUSCL
ou MINMOD).
uvre tridimensionnelle et
satisfont des propriétés physiques fondamentales du transport: localité,
conservation, monotonie, positivité (plus généralement pas de création
d'extrema numériques) et invariance par addition d'une constante au champ de
traceur.
Van Leer (1977) avait en fait proposé une hiérarchie de schémas dont les plus
sophistiqués ont été introduits ultérieurement et indépendamment dans la
communauté météorologique par Russell et Lerner (1981) (schéma des pentes du NASA/GISS) et
Prather (1986).
Avec Alexandre Armengaud alors en thèse au LGGE sous la direction de Christophe
Genthon, nous avons testé dans LMDZ plusieurs de ces schémas (Hourdin et Armengaud, 1999).
Nous avons pu montrer que leurs performances étaient
en fait assez semblables dès lors qu'on les comparait non pas à résolution
spatiale fixée mais à coût numérique équivalent (un schéma plus précis mais
plus coûteux se comporte comme un schéma moins précis mais utilisé sur une
grille plus fine). Nous avons retenu pour le modèle du LMD le schéma le plus
simple (le schéma I dans l'article original de Van Leer souvent appelé MUSCL
ou MINMOD).
Ce travail a donné naissance à la version traceurs du modèle, baptisée un moment LMDZT. En parallèle des schémas d'advection, il a fallu inclure, dans le modèle, le transport associé aux paramétrisations des mouvements non résolus, turbulents ou convectifs. Cette composante est souvent essentielle pour contrôler le transport vertical des espèces. Pour ces schémas, on suit généralement ce qui est fait pour transporter l'humidité ou la température potentielle dans les paramétrisations d'origine. L'introduction des traceurs dans les paramétrisations de la turbulence de couche limite et de la convection nuageuse a été initialement réalisée par Olivier Boucher et Alexandre Armengaud. Cette composante traceurs fait depuis partie intégrante du modèle LMDZ qui permet de transporter un nombre arbitraire de traceurs. De nombreuses applications ont été développées à partir de cette version, à la fois pour la Terre, Mars ou Titan, en lui adjoignant des modules de chimie ou de microphysique des aérosols.
LMDZT a été conçu de façon très modulaire de façon à pouvoir y rajouter facilement des codes de chimie ou des modules d'aérosols. Il est utilisable soit en mode ``branché'' (on-line en anglais), soit en mode débranché, en relisant des fichiers météorologiques issus d'une simulation numérique précédente. Les simulations météorologiques elles-mêmes peuvent être effectuées soit en mode climatique, en laissant le modèle évoluer librement à partir d'une condition initiale unique, soit en le ``guidant'' par des analyses météorologiques. Marie-Angèle Filiberti et Abderrahmane Idelkadi ont largement contribué à fiabiliser et valider l'ensemble des outils développés et présentés ici.
Ce chapitre relativement technique revient à la fois sur la présentation des schémas de transport et sur la description de LMDZT. Nous présentons à la fin quelques exemples de validations ou utilisations du modèle.
Avant d'introduire la composante traceurs, on présente rapidement le modèle LMDZ et notamment la discrétisation des équations de grande échelle sur laquelle s'appuie le transport des traceurs. On en profite pour donner un bref aperçu du contenu des paramétrisations physiques du modèle et des évolutions apportées récemment. 2.2
LMDZ correspond à la seconde génération d'un modèle de climat développé depuis une trentaine d'années au LMD et décrit initialement par Sadourny et Laval (1984). Ce modèle est plus modulaire et flexible2.3que son prédécesseur. Le ``Z" de son nom se réfère à la capacité de raffinement de la grille (Zoom) obtenue grâce à une écriture généralisée de la formulation numérique avec un maillage dont les facteurs d'élongation dans les deux directions horizontales peuvent être choisis arbitrairement.
Comme la plupart des modèles de climat, le modèle LMDZ intègre sur la sphère
et dans le temps les ``équations primitives de la météorologie".
Ces équations sont une version des équations de Navier Stokes simplifiées
en supposant que l'atmosphère est à tout moment en équilibre hydrostatique
sur la verticale et en négligeant les variations verticales de la géométrie
horizontale (hypothèse de couche mince).
Le moment cinétique par rapport à l'axe des pôles est
par exemple calculé en utilisant comme distance à l'axe
![]() - où
- où ![]() est le rayon de la planète
et
est le rayon de la planète
et ![]() la latitude - plutôt que
la latitude - plutôt que
![]() , qui tiendrait compte de
l'altitude
, qui tiendrait compte de
l'altitude ![]() d'une particule d'air au dessus de la surface.
d'une particule d'air au dessus de la surface.
Le modèle du LMD est bâti sur une discrétisation en différences finies de ces équations avec certaines propriétés intéressantes du schéma numérique comme la conservation de la masse, la conservation du moment cinétique par la composante axi-symétrique de l'écoulement et de la vorticité barotrope. On revient sur ces aspects en toute fin de chapitre.
Ces équations ne peuvent pas être intégrées jusqu'à l'échelle visqueuse. En pratique, dans les modèles globaux, on utilise des mailles de quelques dizaines à quelques centaines de kilomètres suivant les applications. L'impact des échelles sous-mailles sur la grande échelle doit donc être représenté au travers de paramétrisations. Il faut également représenter des processus fondamentaux comme le transfert de rayonnement visible et infrarouge dans l'atmosphère, les processus nuageux ou les interactions avec la surface. Dans le jargon des modélisateurs, ces paramétrisations sont regroupées dans la ``physique" du modèle, par opposition avec le code représentant la ``dynamique" de grande échelle. Dans le cas de l'utilisation du modèle de circulation pour d'autres planètes, c'est cette partie physique qui doit être largement modifiée, et notamment le calcul du transfert radiatif.
Dans le modèle LMDZ, les équations primitives sont discrétisées
horizontalement sur une grille-C dans la classification d'Arakawa
(cf. e. g. Kasahara, 1977).
On note ![]() et
et ![]() les coordonnées horizontales :
les coordonnées horizontales :
![]() (resp.
(resp. ![]() ) est une fonction biunivoque de la longitude
) est une fonction biunivoque de la longitude ![]() (resp. de la latitude
(resp. de la latitude ![]() ).
Les variables scalaires
(la température potentielle
).
Les variables scalaires
(la température potentielle ![]() , le géopotentiel
, le géopotentiel ![]() et la pression de surface
et la pression de surface ![]() ) sont évaluées aux points
correspondant à des couples de valeurs entières
) sont évaluées aux points
correspondant à des couples de valeurs entières ![]() .
Le vent zonal est calculé aux points
.
Le vent zonal est calculé aux points
![]() et le vent
méridien aux points
et le vent
méridien aux points
![]() .
La disposition des variables sur la grille est illustrée sur la
Fig. 2.1.
De façon à pouvoir modifier la distribution des longitudes et latitudes
de la grille, on utilise en fait les composantes covariantes
(
.
La disposition des variables sur la grille est illustrée sur la
Fig. 2.1.
De façon à pouvoir modifier la distribution des longitudes et latitudes
de la grille, on utilise en fait les composantes covariantes
(![]() et
et ![]() ) et contravariantes (
) et contravariantes (
![]() et
et
![]() )
du vent définies par
)
du vent définies par
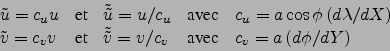 |
(2.1) |
Comme beaucoup de modèles globaux, le modèle du LMD avait initialement
été codé avec une coordonnée verticale de type ![]() . La coordonnée
. La coordonnée
![]() (où
(où ![]() est la pression et
est la pression et ![]() la pression à la surface
au point considéré) est pratique parce qu'elle varie de 1 à la surface à 0
au sommet de l'atmosphère quelque soit le relief
sous-jacent. Cette coordonnée devient cependant problématique plus haut dans
l'atmosphère où on préfère travailler sur des isobares ou, mieux, sur
des isentropes.
Suivant là aussi beaucoup de modèles de climat, nous avons avec Phu LeVan
récrit le modèle en coordonnée hybride
la pression à la surface
au point considéré) est pratique parce qu'elle varie de 1 à la surface à 0
au sommet de l'atmosphère quelque soit le relief
sous-jacent. Cette coordonnée devient cependant problématique plus haut dans
l'atmosphère où on préfère travailler sur des isobares ou, mieux, sur
des isentropes.
Suivant là aussi beaucoup de modèles de climat, nous avons avec Phu LeVan
récrit le modèle en coordonnée hybride ![]() .
La coordonnée hybride est définie de façon implicite
comme donnant la pression dans la couche
.
La coordonnée hybride est définie de façon implicite
comme donnant la pression dans la couche ![]() du modèle sous la forme
du modèle sous la forme
Les niveaux de pression définis par la relation 2.2
correspondent aux interfaces entre les couches du modèle avec ![]() et
et ![]() ,
, ![]() étant le nombre de couches dans le modèle.
La masse d'air contenue dans une maille du modèle comprise entre les
niveaux
étant le nombre de couches dans le modèle.
La masse d'air contenue dans une maille du modèle comprise entre les
niveaux ![]() et
et ![]() est donnée par
est donnée par
| (2.3) |
| (2.4) |
On introduit alors les trois composantes du flux de masse :
| (2.5) |
On ne présente pas ici la discrétisation des équations du mouvements
qui n'a pas changé par rapport à la version ![]() du modèle
et dont ont discute en toute fin de chapitre.
En revanche, l'introduction de la coordonnée hybride à entraîné la
modification du schéma de calcul de la fonction d'Exner
du modèle
et dont ont discute en toute fin de chapitre.
En revanche, l'introduction de la coordonnée hybride à entraîné la
modification du schéma de calcul de la fonction d'Exner
![]() .2.5L'équilibre hydrostatique est intégré verticalement suivant le schéma :
.2.5L'équilibre hydrostatique est intégré verticalement suivant le schéma :
La première utilisation de ce nouveau code hydrodynamique est martienne. Le modèle du LMD est le premier à simuler un cycle saisonnier entier sur la planète rouge (Hourdin et al., 1993). Pendant ce temps le modèle climatique terrestre du LMD poursuit une vie trépidante. La version 4ter, qui donnait des résultats excellents sur la Mousson Indienne (présentez une simulation du modèle à un chercheur authentique du LMD, il commencera par regarder la ``précip'' de juillet sur l'Inde), est progressivement remplacée par les versions 5 et 6. Ces versions sont notamment couplées à SECHIBA pour la végétation et à ORCALIM pour l'océan.
C'est lors d'un séminaire interne du LMD, tenu en la royale abbaye de Fontevraud en 1990, qu'est prise collectivement la décision de faire de ce nouveau code dynamique l'ossature du futur modèle de climat du LMD. Ce choix est motivé par la volonté de disposer d'un outil souple et modulaire, permettant facilement l'échange et le test de modules et de procédures. Cette décision s'inscrit dans l'idée de modélisation communautaire alors dans l'air du temps.
Il faut donc adjoindre au code dynamique un jeu de paramétrisations physiques. Dans un premier temps, la décision est prise de partir de la physique du Centre Européen pour les Prévisions Météorologiques à Moyen Terme. Ce modèle contient en effet le code radiatif Fouquart/Morcrette, développé à l'origine pour le modèle du LMD, et les schémas de nuages d'Hervé LeTreut. Cette décision ne sera finalement pas tenue. Si Laurent Li s'est bien battu pour effectuer les portages nécessaires, le groupe décidera quelques années plus tard de privilégier la continuité avec les versions précédentes.2.7C'est la combinaison de ce nouveau code dynamique et de la réécriture des paramétrisations physiques qui donnera naissance au modèle LMDZ d'aujourd'hui.
On décrit ci-dessous dans ses grandes lignes la version du modèle LMDZ3.3 qui a été utilisée pour les applications "traceurs" décrites dans ce document ainsi que les évolutions apportées au court de la mise au point du modèle couplé IPSLCM4 et qui définissent la version LMDZ4 (Hourdin et al., 2006).
L'effet de la turbulence de petite échelle dans la couche limite est pris en compte au moyen d'une fermeture en super-viscosité avec un flux turbulent proportionnel au gradient vertical de la quantité transportée. La viscosité turbulente dépend du cisaillement vertical du vent et du nombre de Richardson, selon les formules présentées par Laval et al. (1981). Un "contre-gradient" est introduit sur la température potentielle pour permettre un transport de chaleur "en remontant le gradient" dans les couches limites marginalement stables. On revient très largement sur ces aspects relatifs à la couche limite dans le Chapitre 3.
Le code radiatif est celui du modèle du Centre Européen pour les Prévisions Météorologiques à Moyen Terme (Morcrette, 1991). La partie concernant l'absorption et la diffusion du rayonnement solaire est une version raffinée du modèle de Fouquart et Bonnel (1980). La partie infrarouge thermique a été développée par Morcrette et al. (1986). La condensation est paramétrée de façon différente pour la convection profonde et pour les autres nuages. Pour la convection nuageuse, on utilise la paramétrisation développée par Tiedtke (1989). Cette paramétrisation est basée sur une représentation en flux de masse d'une colonne convective nuageuse idéalisée. La colonne atmosphérique est divisée en trois sous-colonnes : une ascendance concentrée, une subsidence rapide associée à la pluie et enfin l'environnement, généralement en subsidence lente. Pour la partie non convective des nuages, on diagnostique une fraction nuageuse et un contenu en eau des nuages en se donnant a priori une fonction de distribution sous-maille de l'eau (Le Treut et Li, 1991). Les nuages ainsi diagnostiqués sont utilisés à la fois pour le calcul radiatif et pour calculer un taux de chauffage et un taux de précipitation. La pluie calculée ainsi peut se réévaporer dans les couches inférieures du modèle. L'eau vapeur et l'eau condensée sont ensuite advectées indépendamment dans la partie dynamique2.8. Le transport de grande échelle de la vapeur d'eau et de l'eau liquide, traité à l'origine avec un schéma amont très diffusif sur l'horizontale et un schéma centré non positif sur la verticale, est maintenant calculé avec les schémas en volumes finis décrits un peu plus loin.
Dans les expériences présentées dans ce document, la température de surface
de la mer est imposée. La conduction thermique dans les sols
continentaux est quant à elle calculée au moyen d'un schéma multi-couches
d'un sol homogène
développé à l'origine pour la version martienne du modèle
(Hourdin et al., 1993).
Si on note ![]() la conduction thermique du sol et
la conduction thermique du sol et ![]() la capacité thermique
volumique, on peut montrer facilement que le flux conductif à la surface
peut s'écrire sous la forme
la capacité thermique
volumique, on peut montrer facilement que le flux conductif à la surface
peut s'écrire sous la forme
![]() et la conduction dans le sol
et la conduction dans le sol
![]() .
.
![]() est appelé inertie thermique et
est appelé inertie thermique et ![]() est une pseudo profondeur
définie par
est une pseudo profondeur
définie par
![]() .
.
Suivant Laval et al. (1981), l'évaporation à la surface est calculée comme
![]() où
où ![]() est la tension de vent en surface,
est la tension de vent en surface,
![]() est l'humidité spécifique de la première couche du modèle atmosphérique
et
est l'humidité spécifique de la première couche du modèle atmosphérique
et ![]() est l'humidité spécifique à saturation pour la température de
surface
est l'humidité spécifique à saturation pour la température de
surface ![]() .
Le coefficient d'aridité
.
Le coefficient d'aridité ![]() peut être soit imposé soit dépendre directement
d'un contenu en eau du sol, calculé au fil du temps en fonction du bilan
entre précipitation et évaporation,
peut être soit imposé soit dépendre directement
d'un contenu en eau du sol, calculé au fil du temps en fonction du bilan
entre précipitation et évaporation,
![]() .
Le modèle utilisé par défaut, dit modèle du saut d'eau (bucket en anglais),
fait l'hypothèse que
.
Le modèle utilisé par défaut, dit modèle du saut d'eau (bucket en anglais),
fait l'hypothèse que ![]() peut
croître jusqu'à une valeur de 150 mm d'eau. Entre 75 et 150 mm, le coefficient
d'aridité
peut
croître jusqu'à une valeur de 150 mm d'eau. Entre 75 et 150 mm, le coefficient
d'aridité ![]() est égal à 1 et l'évaporation est égale à l'évaporation
potentielle. Ce coefficient varie linéairement entre 0 et 1 pour des contenus
en eau du sol variant de 0 à 75 mm.
est égal à 1 et l'évaporation est égale à l'évaporation
potentielle. Ce coefficient varie linéairement entre 0 et 1 pour des contenus
en eau du sol variant de 0 à 75 mm.
La partie physique du modèle est en fait en évolution constante. La description qui en est faite ci-dessus correspond à une vue instantanée de la version qui a servi à développer les aspects liés au transport des traceurs. Sauf mention explicite, c'est cette version de LMDZ3 qui est utilisée dans les simulations présentées dans ce document.
|
|
Depuis, notamment en vue du développement du modèle couplé IPSLCM4, la physique du modèle a évolué de façon significative. Les améliorations principales concernent :
On ne s'appesantit pas dans ce document sur la climatologie du modèle d'atmosphère. On montre cependant une comparaison de la version précédente LMDZ3 du modèle et du nouveau modèle LMDZ4 en ce qui concerne la précipitation (Fig. 2.2 et Fig. 2.3). Les différences principales entre les deux versions proviennent en fait du changement de schéma de convection. L'ancien modèle avait tendance à exagérer l'intensité des précipitations tropicales dans les zones de convergences, notamment à l'Est de Madagascar ainsi que sur l'océan Pacifique. Ce biais est nettement diminué dans le nouveau modèle. La diminution (amélioration) des précipitations sur les continents nord en été (Sibérie, Canada), est elle davantage due au schéma de surface. La détérioration la plus notable avec le nouveau modèle est sans doute la distribution des précipitations de mousson autour de l'Inde en juillet. Lorsqu'on interprète des résultats relatifs à la simulation des concentrations atmosphériques d'aérosols ou d'espèces chimiques, il faut bien sûr garder à l'esprit ces différences quant à la capacité du modèle à simuler correctement le climat.
L'organisation du modèle LMDZ est très étroitement calquée sur cette distinction entre partie "dynamique" - la seule partie où soient pris en compte des échanges horizontaux entre des mailles du modèle - et la partie ``physique" qui peut être vue comme une juxtaposition de ``colonnes" d'atmosphère.
Cette spécificité de la partie physique est exploitée en ce sens que le codage de toutes les paramétrisations est fait avec un indice interne muet qui représente la grille horizontale. Cette organisation est illustrée sur la Fig. 2.4. Chacune des parties, physique et dynamique, a ses propres fichiers de conditions initiales et de sorties.
Cette écriture se prête à la fois à la vectorisation et à la parallélisation des codes. Cette approche permet également de disposer de façon transparente d'une version unidimensionnelle du modèle de circulation. Pour disposer d'un modèle unidimensionnel, il suffit d'écrire un programme dans lequel on initialise des profils météorologiques sur un point particulier du globe et dans lequel on appelle ensuite en boucle le moniteur physique.
Autre atout important, cette conception modulaire permet de gérer en parallèle des ``physiques" différentes interfacées avec le même code dynamique. Ce point est essentiel pour les études menées au LMD sur Mars et sur Titan. Enfin, on peut noter qu'il existe aussi une version bidimensionnelle, latitude-altitude, du noyau dynamique du modèle qui a été abondamment utilisée sur Titan comme on le voit à la fin de ce document.
Le modèle LMDZ est avant tout développé pour des études climatiques.
On effectue alors des intégrations longues, dans lesquelles l'état
initial est vite ``oublié" et les résultats ne s'interprètent qu'en termes
statistiques.
Cependant, notamment pour des aspects de validation, il peut s'avérer
utile de contraindre le modèle à suivre une situation météorologique
observée.
Dans ce mode ``guidé" (on parle souvent de ``nudging" en anglais), les
champs du modèle sont rappelés avec un terme linéaire vers les champs
des analyses ou des réanalyses
| (2.22) |
Une approche intermédiaire a été mise en ![]() uvre dans LMDZ
(Bonazzola, 2001).
Elle consiste à minimiser
une fonction mesurant la distance entre l'état du modèle et les analyses.
Cette approche, qui s'apparente encore davantage à l'assimilation
météorologique opérationnelle,
permet d'introduire, en plus des analyses, des observations
supplémentaires ou des contraintes comme des pénalités sur les modes
de gravité excités par la procédure d'assimilation.
Cette dernière méthode n'est pas utilisée ici.
uvre dans LMDZ
(Bonazzola, 2001).
Elle consiste à minimiser
une fonction mesurant la distance entre l'état du modèle et les analyses.
Cette approche, qui s'apparente encore davantage à l'assimilation
météorologique opérationnelle,
permet d'introduire, en plus des analyses, des observations
supplémentaires ou des contraintes comme des pénalités sur les modes
de gravité excités par la procédure d'assimilation.
Cette dernière méthode n'est pas utilisée ici.
Dans les modèles de chimie-climat comme dans les modèles débranchés transport-chimie, les processus comme la microphysique des aérosols ou les réactions chimiques d'une part et le transport de l'autre sont généralement traités alternativement et séquentiellement. On parle en anglais d'``operator splitting". La partie transport proprement dite peut alors être traitée de façon systématique, indépendamment de l'espèce trace considérée, en assimilant cette espèce à un traceur conservé2.9.
Dans cette partie, on
s'intéresse donc à la modélisation du
transport d'un traceur conservatif (une espèce trace suivant exactement
l'air) et passif (n'affectant pas en retour la météorologie).
L'équation du transport pour un traceur de ce type est simplement
| (2.23) |
| (2.24) |
Dans les applications atmosphériques classiques, l'équation du transport ne peut être résolue jusqu'à l'échelle de la diffusion moléculaire. Cette constatation s'applique d'ailleurs aussi bien à l'observation qu'à la modélisation. Dans les deux cas, on travaille explicitement jusqu'à une échelle donnée mais on traite la petite échelle de façon statistique. Dans le cas d'un modèle numérique, la grande échelle est définie en pratique par le maillage (ou par la troncature pour les modèles spectraux). L'effet des grandeurs sous-mailles sur les variables de grande échelle ne peut être représenté que de façon statistique, au travers de paramétrisations.
Pour séparer échelle explicite et échelle turbulente, on introduit
la notion de moyenne d'ensemble.
La turbulence est considérée comme un processus
aléatoire. Un élément du processus correspond à une réalisation complète
de l'écoulement atmosphérique.
La moyenne d'ensemble d'une grandeur ![]() , qu'on notera
, qu'on notera ![]() ,
est simplement l'espérance mathématique de cette variable.2.10
,
est simplement l'espérance mathématique de cette variable.2.10
Pour introduire proprement le découpage pour un fluide compressible,
il faut introduire en plus une moyenne
pondérée par l'air
![]() .
La fluctuation turbulente par rapport à cette moyenne
.
La fluctuation turbulente par rapport à cette moyenne
![]() obéit à l'identité
obéit à l'identité
![]() .
.
Si on note ![]() le champ de vent et
le champ de vent et ![]() la concentration massique d'un
traceur conservatif (
la concentration massique d'un
traceur conservatif (![]() ),
l'équation de transport non visqueux peut s'écrire soit
),
l'équation de transport non visqueux peut s'écrire soit
En prenant la moyenne d'ensemble de la forme conservative et en remarquant
que
| (2.28) |
Ci-dessous, on présente en détail les schémas introduits pour traiter du transport de grande échelle ainsi que les paramétrisations des termes turbulents calquées sur les paramétrisations d'origine du code LMDZ. Dans le chapitre suivant, on présente en détail un travail spécifique mené sur le transport turbulent dans la couche limite convective.
De nombreuses méthodes ont été développées au cours des dernières décennies pour représenter l'advection, c'est à dire les parties non turbulentes des Eqs 2.30 ou 2.29 formellement équivalentes aux Eqs 2.25 et 2.27.
On distingue notamment :
Les formulations en ``volumes finis" présentent l'avantage très important d'être conservatives par nature, dès lors que le même flux est utilisé pour les volumes en amont et en aval de l'interface considérée.
Pour le plus connu de ces schémas, introduit par Godunov (1959),
![]() est simplement estimé comme le produit de
est simplement estimé comme le produit de ![]() par la valeur de
par la valeur de
![]() dans le volume amont (dans la maille d'où l'air provient).
Ce schéma simple, souvent appelé schéma amont,
garantit
dans le volume amont (dans la maille d'où l'air provient).
Ce schéma simple, souvent appelé schéma amont,
garantit
Van Leer (1977) a proposé d'utiliser, pour la valeur amont de ![]() , non pas
la valeur moyenne dans la maille amont mais une valeur extrapolée
à la frontière de celle-ci, en utilisant une approximation
polynomiale de la distribution sous-maille du traceur dans la maille
amont.
Deux des schémas proposés par Van Leer en 1977 ont été introduits
apparemment indépendamment dans la littérature météorologique par
Russell et Lerner (1981) - le schéma III dans la classification de Van Leer -
et Prather (1986) - le schéma VI -.
Alors que dans son article original, Van Leer conclut que la complexité
du schéma VI est trop grande par rapport au gain en précision, ce schéma
est devenu une référence dans la communauté météorologique.
, non pas
la valeur moyenne dans la maille amont mais une valeur extrapolée
à la frontière de celle-ci, en utilisant une approximation
polynomiale de la distribution sous-maille du traceur dans la maille
amont.
Deux des schémas proposés par Van Leer en 1977 ont été introduits
apparemment indépendamment dans la littérature météorologique par
Russell et Lerner (1981) - le schéma III dans la classification de Van Leer -
et Prather (1986) - le schéma VI -.
Alors que dans son article original, Van Leer conclut que la complexité
du schéma VI est trop grande par rapport au gain en précision, ce schéma
est devenu une référence dans la communauté météorologique.
Les principes de dérivation de ces différents schémas sont exposés ci-dessous.
En dimension 1 et après intégration sur un pas de temps, les
Eq. 2.31 et 2.32 s'écrivent simplement
Si on connaît complètement la distribution spatio-temporelle du vent, de la
densité de l'air et de la concentration de traceur, on a
| (2.35) |
| (2.36) |
| (2.37) |
| (2.38) |
Dans la présentation faite ici, on considère que les transferts
de masse ![]() sont connus à chaque instant et sur tout le maillage.
L'évolution temporelle de la masse d'air
sont connus à chaque instant et sur tout le maillage.
L'évolution temporelle de la masse d'air
![]() est donc également complètement déterminée.
La seule chose qui reste à estimer est le flux de traceur.
est donc également complètement déterminée.
La seule chose qui reste à estimer est le flux de traceur.
De façon générale, ce flux ![]() peut être écrit comme le produit
du transfert de masse
peut être écrit comme le produit
du transfert de masse ![]() par la valeur moyenne de la concentration
du traceur
par la valeur moyenne de la concentration
du traceur
![]() dans l'air qui traverse l'interface au cours du pas
de temps.
dans l'air qui traverse l'interface au cours du pas
de temps.
![\includegraphics[width=16cm]{lmdzt/FIGURES/schema2.eps}](img222.png) |
La méthode proposée par Van Leer consiste à approximer la distribution
sous-maille par un polynôme pour lequel le calcul de
![]() - et
donc du transfert de traceur - peut être fait exactement.
Le principe et les notations sont illustrées sur la Fig. 2.5
pour le cas d'un polynôme du premier degré.
Avec ces notations, les valeurs moyennes de
- et
donc du transfert de traceur - peut être fait exactement.
Le principe et les notations sont illustrées sur la Fig. 2.5
pour le cas d'un polynôme du premier degré.
Avec ces notations, les valeurs moyennes de ![]() et
et ![]() après un pas de temps
d'advection s'écrivent simplement
après un pas de temps
d'advection s'écrivent simplement
Pour des valeurs positives de ![]() et
et ![]() ,
l'Eq. 2.39 peut se récrire
,
l'Eq. 2.39 peut se récrire
Un des points essentiels de l'article original de Van Leer (1977) est
de remarquer qu'on peut garantir la monotonie du schéma d'advection
- en dimension 1, une distribution monotone reste monotone après advection -
en imposant que ![]() prenne une valeur intermédiaire entre les
deux valeurs voisines de
prenne une valeur intermédiaire entre les
deux valeurs voisines de ![]() dans les régions où
dans les régions où ![]() est monotone.
est monotone.
Supposons pour fixer les idées que
![]() et
et ![]() .
La condition ci-dessus s'écrit simplement
.
La condition ci-dessus s'écrit simplement
Si on rajoute en plus la condition que
![]() (distribution sous-maille constante)
quand
(distribution sous-maille constante)
quand ![]() est un extremum, on interdit la croissance des extrema.
Ceci implique de fait la positivité du schéma et interdit la création
d'oscillations provenant du caractère dispersif du schéma numérique
(provenant de l'advection avec des vitesses différentes des
différentes composantes de fourier de la distribution, cf. e. g. Rood, 1987).
est un extremum, on interdit la croissance des extrema.
Ceci implique de fait la positivité du schéma et interdit la création
d'oscillations provenant du caractère dispersif du schéma numérique
(provenant de l'advection avec des vitesses différentes des
différentes composantes de fourier de la distribution, cf. e. g. Rood, 1987).
Noter aussi qu'avec les définitions ci-dessus, une distribution uniforme
de traceur sera inchangée par l'advection, même avec des champs de vents
divergents (on s'en convainc en remplaçant
![]() et
et
![]() par une valeur constante dans l'Eq. 2.39).
par une valeur constante dans l'Eq. 2.39).
Dans les dérivations ci-dessus, on a supposé implicitement que le pas
de temps était suffisamment petit pour éviter de transférer plus que la
maille d'une cellule en un pas de temps (nombre de Courant ![]() inférieur
à 1). Si le flux de masse est exactement égal à la masse d'air dans le
volume amont, on calculera la distribution de traceur exactement, quelque
soit l'approximation choisie pour la distribution sous-maille.
inférieur
à 1). Si le flux de masse est exactement égal à la masse d'air dans le
volume amont, on calculera la distribution de traceur exactement, quelque
soit l'approximation choisie pour la distribution sous-maille.
La première approximation consiste à supposer que le traceur est constant
dans chaque maille (polynôme de degré zéro).
![]() est alors simplement la valeur de
est alors simplement la valeur de ![]() dans la maille amont
(
dans la maille amont
(
![]() si
si ![]() et
et ![]() sinon).
Ce schéma proposé à l'origine par Godunov (1959) est bon marché, positif
et monotone mais au prix d'une diffusion numérique très forte.
La diffusivité du schéma peut d'ailleurs être quantifiée.
Dans le cas d'un champ de vent non divergent
(
sinon).
Ce schéma proposé à l'origine par Godunov (1959) est bon marché, positif
et monotone mais au prix d'une diffusion numérique très forte.
La diffusivité du schéma peut d'ailleurs être quantifiée.
Dans le cas d'un champ de vent non divergent
(
![]() cste à une dimension),
le schéma 2.39 s'écrit
cste à une dimension),
le schéma 2.39 s'écrit
| (2.44) |
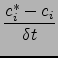 |
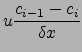 |
(2.45) | |
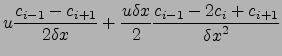 |
(2.46) |
Pour passer à un ordre supérieur, on
suppose que la distribution sous-maille est linéaire avec une pente
![]() donnant les valeurs aux bords gauche et droit de la maille
donnant les valeurs aux bords gauche et droit de la maille ![]() comme
comme
![]() (voir l'illustration de la Fig. 2.5).
(voir l'illustration de la Fig. 2.5).
Dans ce cas,
![]() est donné par
est donné par
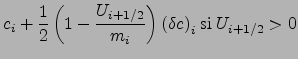 |
(2.47) | ||
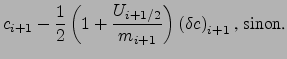 |
(2.48) |
Différents schémas ont été proposés (Van Leer, 1977,1979)
correspondant à différentes estimations de
![]() , dont deux schémas
particulièrement intéressants, l'un pour son faible coût et l'autre pour
sa précision.
, dont deux schémas
particulièrement intéressants, l'un pour son faible coût et l'autre pour
sa précision.
![\includegraphics[width=9.cm]{lmdzt/FIGURES/schema3.eps}](img259.png)
![\includegraphics[width=7.cm]{lmdzt/FIGURES/1dn.eps}](img260.png) |
Dans le schéma I de Van Leer, la pente est simplement estimée à chaque pas
de temps par différences finies
(
![]() ) comme l'illustre
le graphique a de la Fig. 2.6.
Ce schéma peut être considéré comme une version volumes-finis du schéma de
From (1968).
) comme l'illustre
le graphique a de la Fig. 2.6.
Ce schéma peut être considéré comme une version volumes-finis du schéma de
From (1968).
Dans le second schéma, la pente au pas de temps ![]() dans une maille
donnée est calculée à partir de la distribution en ligne brisée résultant de
l'advection au temps
dans une maille
donnée est calculée à partir de la distribution en ligne brisée résultant de
l'advection au temps ![]() (illustration sur le graphique b de la Fig. 2.6).
La nouvelle distribution sous-maille
minimise la distance quadratique par rapport à cette distribution.
Ce second schéma (le schéma III dans l'article original de Van Leer)
a en fait été redécouvert quelques années plus tard par
Russell et Lerner (1981)2.13
dans un contexte météorologique tridimensionnel.
Ce schéma a été popularisé dans le modèle de circulation générale
du NASA/GISS. On l'appelle souvent
schéma des pentes (``slopes scheme" en anglais). On retiendra ce nom dans ce
qui suit.
(illustration sur le graphique b de la Fig. 2.6).
La nouvelle distribution sous-maille
minimise la distance quadratique par rapport à cette distribution.
Ce second schéma (le schéma III dans l'article original de Van Leer)
a en fait été redécouvert quelques années plus tard par
Russell et Lerner (1981)2.13
dans un contexte météorologique tridimensionnel.
Ce schéma a été popularisé dans le modèle de circulation générale
du NASA/GISS. On l'appelle souvent
schéma des pentes (``slopes scheme" en anglais). On retiendra ce nom dans ce
qui suit.
On présente, sur le graphique c de la Fig. 2.6, un exemple typique de calcul d'advection unidimensionnel avec le schéma de Godunov, Van Leer I et le schéma des pentes. Le schéma des pentes est bien sûr le plus précis mais la différence principale se situe entre le schéma de Godunov, extrêmement diffusif, et les deux autres. On voit également apparaître pour les deux schémas d'ordre 2 des oscillations provenant de la non monotonie du schéma et la création de valeurs négatives.
L'un des intérêts principaux du travail de Van Leer (1977) réside dans la possibilité qu'il offre d'assurer facilement la monotonie des schémas. Une première façon consiste à appliquer directement la contrainte explicitée à la fin de la Section 2.3.3.
Pour les schémas du second ordre,
Van Leer (1977) propose aussi une condition suffisante à la fois plus
brutale et plus simple. Il suffit, pour que le schéma soit monotone, d'imposer
que la distribution dans une maille ![]() soit entièrement comprise entre
les valeurs moyennes des deux mailles adjacentes et que la pente soit
du même signe que dans ces deux mailles (à noter que ce dernier critère
est automatiquement satisfait par le schéma I).
Cette condition suffisante peut s'exprimer facilement comme un
limiteur de pente.
Pour le schéma I, la formulation complète du calcul de la pente avec limiteur
s'écrit simplement
soit entièrement comprise entre
les valeurs moyennes des deux mailles adjacentes et que la pente soit
du même signe que dans ces deux mailles (à noter que ce dernier critère
est automatiquement satisfait par le schéma I).
Cette condition suffisante peut s'exprimer facilement comme un
limiteur de pente.
Pour le schéma I, la formulation complète du calcul de la pente avec limiteur
s'écrit simplement
![\includegraphics[width=15.cm]{lmdzt/FIGURES/schema4b.eps}](img265.png) |
L'effet de l'application d'un limiteur fort (décrit ici) ou d'un limiteur faible (application directe des Eq. 2.42 et Eq. 2.43), qui correspondent respectivement aux Eq. (66) et (74) données par Van Leer (1977) est illustré sur la Fig. 2.7a. Un test numérique de l'impact de ces limiteurs est montré sur les Fig. 2.7c et d. Le limiteur fort dégrade de façon significative la précision du schéma des pentes tandis que le limiteur faible corrige ce schéma de façon sélective au niveau des oscillations, sans émousser par exemple le sommet de la gaussienne. Pour le schéma I, la différence entre les deux limiteurs est nettement plus marginale.
Il existe une alternative élégante à l'Eq. 2.49 qui consiste à
utiliser la moyenne géométrique des deux pentes voisines
La description de la distribution sous-maille du traceur peut être encore améliorée en utilisant un polynôme du second ordre. L'équivalent du schéma I de Van Leer (le schéma IV dans l'article original) consiste à évaluer les coefficients de ce polynôme par différences finies à partir des valeurs moyennes dans les mailles. Van Leer a attaché peu d'importance à ce schéma qui présente par exemple comme défaut de n'être pas plus précis que le schéma I pour un nombre de Courant de 0,5. Cependant, pour des valeurs plus petites, il peut devenir nettement plus précis. Comme le schéma I, ce schéma présente l'intérêt de n'utiliser qu'un traceur par point de grille. Woodward et Colella (1981) ont développé une alternative au schéma IV en utilisant un filtre non-linéaire assez élaboré permettant de renforcer les pentes en cas de choc (se reporter également à Woodward et Colella, 1984; Colella et Woodward, 1984). La méthode qui en résulte a été baptisée Piecewise Parabolic Method. Elle a été utilisée pour les applications atmosphériques par exemple par Carpenter et al. (1990), Lin et Rood (1996) ou Vautard et al. (2001). Dans ce manuscrit on ne présente pas les résultats avec PPM. Mais des tests ont été réalisés récemment avec ce schéma qui se comporte de façon assez similaire au schéma des pentes pour un coût numérique intermédiaire entre les schémas I et III (pentes) en termes de temps de calcul. Le coût en stockage est le même que pour le schéma I.
L'équivalent à l'ordre 3 du schéma III de Van Leer est le schéma VI
connu dans la littérature météorologique sous le nom de schéma
de Prather (1986).
Le schéma de Prather est évidemment beaucoup plus précis que tous les
schémas présentés jusque là comme le montrent les illustrations de la
section suivante.
Cependant, il nécessite la conservation de 10 traceurs indépendants :
la moyenne, les 3 pentes dans les 3 directions d'espace ![]() ,
, ![]() ,
,
![]() et les 6 moments du second ordre
et les 6 moments du second ordre ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() et
et ![]() .
Il est également nécessaire de lui adjoindre des algorithmes du type limiteurs
de pente pour éviter complètement les oscillations numériques ou les valeurs
négatives.
.
Il est également nécessaire de lui adjoindre des algorithmes du type limiteurs
de pente pour éviter complètement les oscillations numériques ou les valeurs
négatives.
L'introduction des schémas en volumes finis est relativement facile dans le modèle de circulation générale LMDZ car les flux de masse sont déjà définis sur une grille décalée. Ces flux de masse sont ceux utilisés dans la partie météorologique pour intégrer l'équation de continuité pour l'air, à savoir l'Eq. 2.33 ou l'Eq. 2.88 donnée plus loin.
![\includegraphics[height=8cm]{lmdzt/FIGURES/schemsplit.eps}](img277.png)
![\includegraphics[height=9cm]{lmdzt/FIGURES/split.eps}](img278.png) |
Les présentations ci-dessus ont été faites avec une seule dimension d'espace. Une solution naturelle pour passer en 3 dimensions consiste à calculer d'abord les flux dans chaque dimension puis à calculer la divergence des flux.
Une alternative classique consiste à faire trois calculs d'advection, successivement dans les trois directions. On parlera de flux alternés ou de directions alternées.
Cette seconde méthode est curieusement plus précise dans le cas d'une advection
en diagonale par rapport au maillage.
Ceci est illustré sur la Fig. 2.8 pour une configuration bidimensionnelle.
Si on considère un pas de temps d'advection, le calcul direct ne tient
pas compte de l'air passant directement dans la maille située en
diagonale par rapport à la maille du milieu (le petit carré sombre
sur les figures). En revanche, cet air est compté deux fois, une fois dans
l'advection en ![]() et une fois dans l'advection en
et une fois dans l'advection en ![]() .
Ceci produit une très forte diffusion latéral en réduisant la propagation
dans la direction du mouvement. En partant d'un panache gaussien, la
distribution obtenue s'étire dans la direction transverse à l'écoulement
(en haut à droite sur la figure).
.
Ceci produit une très forte diffusion latéral en réduisant la propagation
dans la direction du mouvement. En partant d'un panache gaussien, la
distribution obtenue s'étire dans la direction transverse à l'écoulement
(en haut à droite sur la figure).
Au contraire, pour l'advection en flux alternés, le carré sombre commence par passer dans la maille située à droite de la maille d'origine puis en haut et arrive bien finalement dans la maille située en diagonale par rapport à la maille d'origine. Si on pouvait à chaque instant connaître exactement la distribution sous-maille du traceur, on aurait donc un calcul exact.
Dans la méthode des flux alternés, on intègre successivement non seulement l'équation d'advection du traceur (Eq. 2.39) mais aussi l'advection de transport de l'air (Eq. 2.40)2.14. Avec cette approche, une distribution uniforme de traceur est inchangée par l'advection indépendamment du caractère divergent ou non du champ de vent (Lin et Rood, 1996, montrent que ce n'est pas garanti par toutes les formulations en flux alternés).
Cette approche en flux alternés est utilisée assez systématiquement dans les calculs d'advection en volumes finis (Van Leer, 1979; Prather, 1986; Allen et al., 1991; Russell et Lerner, 1981).
On utilise ici la séquence proposée par Russell et Lerner (1981) :
| Direction | pas de temps |
| X | |
| Y | |
| Z | |
| Y | |
| X |
Si on veut ne travailler qu'avec des nombres de Courant
(
![]() ou
ou ![]() ) inférieurs à 1,
le raffinement de la discrétisation près des pôles, inhérent aux
grilles globales longitudes-latitudes, nécessite l'utilisation de pas de temps
extrêmement petits dans la direction longitudinale.
Une possibilité pour résoudre ce problème consiste à découper encore
davantage le pas de temps pour l'advection longitudinale.
) inférieurs à 1,
le raffinement de la discrétisation près des pôles, inhérent aux
grilles globales longitudes-latitudes, nécessite l'utilisation de pas de temps
extrêmement petits dans la direction longitudinale.
Une possibilité pour résoudre ce problème consiste à découper encore
davantage le pas de temps pour l'advection longitudinale.
Il existe une alternative utilisant le fait que le calcul est
exact pour un nombre de courant de 1. Dans ce cas en effet, le flux
est simplement le produit du flux de masse par la concentration
moyenne du traceur dans la maille amont.
Si le nombre de courant est plus grand que 1,
(pour fixer les idées, si on prend ![]() et
et
![]() )
on peut calculer le transfert de traceur comme la somme de la quantité
de traceur dans la maille amont (
)
on peut calculer le transfert de traceur comme la somme de la quantité
de traceur dans la maille amont (![]() ) et de la quantité
de traceur transférée depuis la maille
) et de la quantité
de traceur transférée depuis la maille ![]() avec un flux
de masse
avec un flux
de masse ![]() .
.
De façon générale, pour
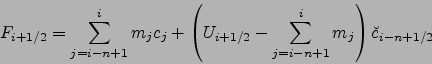 |
(2.52) |
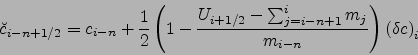 |
(2.53) |
Cette façon de voir les schémas en volumes finis présente de fortes analogies avec les approches semi-Lagrangiennes pour lesquelles ont prédit la valeur ponctuelle en un point du maillage en remontant en amont la trajectoire de la particule. Cette analogie a conduit Lin et Rood (1996) à introduire la notion de flux-form Semi-Lagrangian method. A noter qu'en parallèle, les adeptes des schémas semi-Lagrangiens classiques modifient leurs formulations pour garantir la conservation et les font ressembler de plus en plus à des schémas en volumes finis (e. g. Yabe et al., 2001).
On pourrait de façon générale et pour un pas de temps aussi grand qu'on veut,
estimer les contours du maillage transportés à rebours sur un
pas de temps. A partir d'une estimation polynomiale des distributions sous
mailles, comme celles proposées par Van Leer, on pourrait calculer
alors la distribution de traceur sur ce maillage déformé par le transport
à rebours.
Mais on paie vite en complexité du schéma et en coût informatique (introduction
de branchements supplémentaires et gestion de la mémoire,
particulièrement pénalisant
sur des ordinateurs vectoriels ou parallèles) ce qu'on gagne avec l'utilisation
d'un pas de temps plus long. De plus, on ne tient pas forcément à utiliser
des pas de temps plus longs que les constantes caractéristiques des
autres processus (transport turbulent dans la couche limite, chimie, etc...).
On restreint donc ici le traitement des nombres de Courant plus grands
que 1 à la direction longitudinale pour traiter spécifiquement le problème
de raffinement du maillage en longitude à l'approche des pôles.
Pour une résolution typique du modèle LMDZT, avec une grille
d'environ 100 000 points et un pas de temps de 15 minutes,
la condition ![]() n'est rencontrée typiquement que quelques dizaines
de fois par pas de temps ce qui rend le coût marginal raisonnable.
n'est rencontrée typiquement que quelques dizaines
de fois par pas de temps ce qui rend le coût marginal raisonnable.
Dans le modèle du LMD, les pôles correspondent à des centres de mailles triangulaires. La dimension de ces mailles est 2 fois plus petite dans la direction méridienne que celle des mailles normales. Toutes ces mailles ne sont en fait pas indépendantes et on impose que les valeurs scalaires (pression de surface, température, concentration de traceurs) soient toutes identiques. L'évolution de la masse d'air ou de la quantité d'un traceur au pôle est estimée à partir de la convergence totale des flux méridiens. En fait, on peut considérer le pôle comme un volume de contrôle consistant en un polygone avec autant d'arêtes que le nombre de points longitudinaux de la grille.
Il semble impossible de garantir strictement la monotonie du schéma en conservant des pentes non nulles pour ces mailles polaires. On retient donc aux pôles un schéma de Godunov.
La Fig. 2.9 montre un exemple d'advection transpolaire d'une distribution sinusoïdale avec un écoulement en rotation solide le long du méridien de Greenwich. Les figures du bas montrent le résultat de l'advection après une révolution complète (la solution exacte, à gauche, est identique à la distribution initiale). La distribution obtenue avec le schéma I (cas a) est allongée dans la direction méridienne à cause de la diffusion numérique, dans la direction de l'écoulement. Pour la même résolution, le schéma de Prather est beaucoup moins diffusif. La forme des iso-lignes est cependant légèrement altérée par le passage au pôle. Pour ces calculs, on s'est arrangé pour que le nombre de Courant soit toujours inférieur à 1. Le dernier exemple sur la droite (cas b) correspond à un calcul avec le schéma I utilisant un pas de temps beaucoup plus grand, avec un nombre de Courant qui atteint 8 dans la direction longitudinale près du pôle. On remarque que les résultats sont plutôt meilleurs que ceux du cas a à cause du plus petit nombre de pas de temps nécessaire (160 au lieu de 16000).
![\includegraphics[width=16cm]{lmdzt/FIGURES/pole.eps}](img289.png) |
Dans cette section, nous présentons des tests bidimensionnels des schémas d'advection tels qu'ils sont codés dans le modèle LMDZT. On teste le schéma de Godunov, le schéma I de Van Leer, le schéma des pentes et le schéma de Prather. Pour le schéma I, on utilise le limiteur fort. Pour les schémas de pentes et de Prather, on assure seulement la positivité en utilisant un limiteur de flux (suivant Prather, 1986, on se contente d'imposer de ne pas sortir plus de traceur d'une maille que ce qu'elle contient). Les schémas de Pentes et de Prather que nous utilisons ont été optimisés et interfacés avec le modèle ancien du LMD par Pascal Simon et Christophe Genthon.
On insiste dans les tests présentés ci-dessous sur le rapport entre précision et coût numérique. On montre en effet que l'arbitrage entre une résolution plus fine, qui rend tous les schémas plus précis, et l'utilisation d'un schéma intrinsèquement plus précis, comme Prather, n'est pas évident et peut dépendre du type de machine utilisé ou d'autres considérations relatives à d'autres composantes du modèle.
De façon générale, on peut gagner en précision en utilisant une résolution spatiale plus fine, ce qui se fait évidemment au prix d'un coût numérique plus grand. Une question pratique importante en termes d'efficacité des schémas est de savoir ce qu'on gagne en changeant de schéma d'advection à coût numérique inchangé. Puisque notre but est l'advection tridimensionnelle dans un modèle de circulation générale, il faut d'abord se faire une idée du coût relatif des différents schémas dans une telle configuration.
La comparaison la plus facile est celle de l'occupation en mémoire. Les schémas de Godunov, Van Leer I et PPM ne nécessitent de conserver qu'une variable indépendante par maille et par champ de traceur.
Les schémas des pentes et de Prather sont nettement plus coûteux avec respectivement 4 et 10 variables d'état pour décrire un traceur physique.
La comparaison en termes de rapidité est moins évidente et peut dépendre du type de machine utilisé. Des test sur machines scalaires (stations SUN) et vectorielles montrent qu'il y a typiquement un facteur 2 entre le schéma I et les pentes et entre les pentes et Prather.
Les machines vectorielles favorisent de façon générale l'utilisation de schémas plus grossier sur des grilles plus fines. Pour les test présentés ci-dessous, effectués sur un CRAY-90, les pentes ont exactement le même coût numérique pour une grille horizontale de 60 par 43 points que le schéma I de Van Leer pour une grille de 120 par 85 points.
On voit que le fait de doubler la résolution horizontale dans chaque direction rend le schéma I équivalent à celui des pentes à la fois en termes de stockage et en termes de rapidité sur une machine vectorielle. De même, les pentes en résolution double sont comparables à Prather sur une grille deux fois plus grossière.
De façon générale, les machines scalaires sont plus favorables aux schémas plus précis.
Nous présentons ici des tests numériques bidimensionnels effectués avec un champ de vent analytique présentant une rotation différentielle et pour lequel l'advection peut être calculée exactement. Ce test est effectué sur la sphère en utilisant la discrétisation du modèle de circulation, pour permettre de valider directement les codes utilisés dans le modèle de circulation générale.
Pour un champ de vent horizontal non divergent dans le plan
longitude-latitude (![]() ,
, ![]() ), les composantes zonale (
), les composantes zonale (![]() ) et
méridienne (
) et
méridienne (![]() ) du vent satisfont la relation suivante :
) du vent satisfont la relation suivante :
| (2.54) |
En suivant une trajectoire (valeur constante de ![]() ), la vitesse méridienne
), la vitesse méridienne
![]() peut être récrite en combinant les équations
2.55 et 2.57 :
peut être récrite en combinant les équations
2.55 et 2.57 :
| (2.58) |
![\begin{displaymath}
-\alpha\int \mbox{ sign}{\lambda} \mbox{d}t =
\int \frac{\co...
...rcsin\left(\frac{\sin\phi}{\sqrt{1-\Psi/(aU_0)}}\right)\right]
\end{displaymath}](img302.png) |
(2.59) |
![\includegraphics[width=16cm,trim=0 10 0 0]{lmdzt/FIGURES/uvn.eps}](img304.png) |
Sur le graphique en haut à gauche de la Fig. 2.10, on montre à la fois la distribution initiale du traceur, une gaussienne ne dépendant que de la longitude, et le champ de vent (dans une unité arbitraire). Toujours en haut, les figures à droite montrent l'évolution exacte du traceur sous l'effet de l'advection. La rotation est plus rapide au centre qu'aux bords du domaine, ce qui produit cette forme en spirale et une filamentation.
Pour les tests numériques on utilise trois résolutions :
![]() (résolution pleine),
(résolution pleine), ![]() (résolution 1/2)
et
(résolution 1/2)
et ![]() (résolution 1/3).
Le pas de temps
est choisi suffisamment petit pour que le nombre de Courant reste toujours
plus petit que 1 (le traitement spécial en longitude n'étant codé
que pour le schéma I de Van Leer).
L'état final montré sur les figures correspond à une révolution
complète au centre du maillage ce qui nécessite un nombre
de pas de temps de 4000, 6000 et 12000 pour les différentes résolutions
horizontales testées.
(résolution 1/3).
Le pas de temps
est choisi suffisamment petit pour que le nombre de Courant reste toujours
plus petit que 1 (le traitement spécial en longitude n'étant codé
que pour le schéma I de Van Leer).
L'état final montré sur les figures correspond à une révolution
complète au centre du maillage ce qui nécessite un nombre
de pas de temps de 4000, 6000 et 12000 pour les différentes résolutions
horizontales testées.
La reconstruction très fine des filaments (avec des valeurs maximum dépassant 0,9 pour une valeur initiale de 1) avec le schéma de Prather en pleine résolution est très impressionnante. Cependant, le schéma des pentes fait plutôt mieux à cette résolution que Prather dans une résolution deux fois plus grossière dans chaque direction horizontale. On observe la même chose entre le schéma I de Van Leer et le schéma des pentes.
Donc, si on change la résolution dans seulement deux directions, le schéma I se comporte plutôt mieux que les pentes en terme de rapport qualité/coût.
Si on change de résolution dans les trois directions, la comparaison doit être faite entre la pleine résolution et la résolution intermédiaire avec un avantage significatif pour les schémas précis.
Il est enfin intéressant de noter la différence flagrante de performances entre les schémas de Godunov et le schéma I en dépit d'un coût équivalent en termes de stockage.
Les schémas en volumes finis proposés par Van Leer (1977)
conduisent facilement à des mises en ![]() uvre
tridimensionnelles qui satisfont des propriétés essentielles du
transport comme
uvre
tridimensionnelles qui satisfont des propriétés essentielles du
transport comme
En pratique, on constate que les schémas plus sophistiqués se comportent mieux, mais au pris d'un coût numérique additionnel du même ordre que celui qu'aurait entraîné l'utilisation d'une grille plus fine. A noter qu'il se peut que les schémas deviennent à partir d'un certain stade moins diffusifs que l'atmosphère elle-même. C'est particulièrement vrai pour la basse troposphère, dans laquelle la turbulence de couche limite induit une très forte diffusion verticale, qui, couplée à des cisaillements importants du vent horizontal, conduit aussi à une forte dispersion horizontale effective. Les tests présentés plus loin illustrent ce point.
Pour finir, il faut noter que nous avons présenté ici les schémas dérivés à l'origine par Van Leer. Le schéma PPM qui a également été testé dans LMDZ (résultats non présentés) semble supérieur à coût numérique égal (en tous cas en termes de stockage) à ces schémas d'origine.
L'ensemble des schémas décrits ci-dessus a été introduit dans le modèle LMDZ. Le schéma I de Van Leer a été retenu en standard pour sa robustesse et sa simplicité mais ce choix ne doit pas être considéré comme définitif et doit être reconsidéré en fonction du problème abordé.
Pour le terme turbulent
![]() , on distingue en
fait trois contributions décrites ci-dessous.
, on distingue en
fait trois contributions décrites ci-dessous.
Dans la version standard de LMDZ, la turbulence de couche limite est
traitée comme une super-viscosité ou viscosité turbulente.
Dans ces formulations, comme pour la viscosité moléculaire, le flux
d'une quantité transportée est proportionnel (avec un coefficient
négatif) au gradient local de la quantité en question.
Dans la couche limite planétaire, et si on s'intéresse à l'écoulement
à grande échelle, le terme vertical domine de loin ce flux qui s'écrit alors
| (2.60) |
De nombreux développements ont été consacrés ces dernières décennies
à la paramétrisation de la convection nuageuse (profonde ou peu profonde),
notamment dans le cadre de la modélisation du climat.
Les paramétrisations à la mode sont basées sur des approches
dites en flux de masse
(Arakawa et Schubert, 1974; Emanuel, 1991; Tiedtke, 1989).
Elles ont en commun d'expliciter des ascendances concentrées, sensées
représenter le c![]() ur des nuages convectifs. Dans ces ascendances,
l'air monte rapidement sous l'effet de sa propre
flottabilité, renforcée dans le nuage par le dégagement de chaleur latente.
ur des nuages convectifs. Dans ces ascendances,
l'air monte rapidement sous l'effet de sa propre
flottabilité, renforcée dans le nuage par le dégagement de chaleur latente.
Certaines de ces paramétrisations considèrent un spectre complet de panaches ascendants. Dans les développements présentés ici, on utilise la paramétrisation de Tiedtke (1989) qui sépare la colonne atmosphérique en trois sous-colonnes : une pour les ascendances, une pour les descentes précipitantes et un troisième compartiment pour l'environnement dans lequel se produit une subsidence compensatoire plus lente.
L'ascendance est caractérisée par un flux de masse
![]() qui échange de l'air avec l'environnement.
Cet échange est prescrit au travers d'un entraînement
qui échange de l'air avec l'environnement.
Cet échange est prescrit au travers d'un entraînement ![]() et
d'un détraînement
et
d'un détraînement ![]() .
Pour les descentes précipitantes, ont définit de même un flux de masse
.
Pour les descentes précipitantes, ont définit de même un flux de masse
![]() , un entraînement
, un entraînement ![]() et un détraînement
et un détraînement ![]() .
.
La colonne convective est supposée stationnaire de sorte que la conservation
de la masse d'air entre les différents compartiments s'écrit
| (2.61) |
| (2.62) |
Pour l'inclusion de la composante traceur, on fait les approximations
suivantes en suivant la philosophie du schéma d'origine :
on suppose que le traceur est dans un régime stationnaire à la fois dans
l'ascendance et dans les descentes précipitantes.
On suppose de plus que la fraction
de la maille couverte par ces deux compartiments est suffisamment faible
pour qu'on puisse confondre la concentration dans l'environnement ![]() avec la concentration moyenne dans la maille (
avec la concentration moyenne dans la maille (![]() ou
ou ![]() ).
).
Sous ces hypothèses, la concentration dans l'ascendance
![]() est donnée par
est donnée par
| (2.63) |
| (2.64) |
| (2.65) |
Afin d'assurer la stabilité numérique de ce schéma, les différents
termes de transport (de la forme ![]() ) sont traités avec un schéma
amont du premier ordre.
2.15La diffusion numérique n'est pas un problème
ici puisque le processus physique lui-même est très diffusif.
Les erreurs numériques associées sont certainement plus faibles que les
incertitudes sur l'intensité et la description des échanges d'air dans
la colonne convective.
) sont traités avec un schéma
amont du premier ordre.
2.15La diffusion numérique n'est pas un problème
ici puisque le processus physique lui-même est très diffusif.
Les erreurs numériques associées sont certainement plus faibles que les
incertitudes sur l'intensité et la description des échanges d'air dans
la colonne convective.
Les termes turbulents associés à du mélange vertical sont souvent nettement plus important que les termes horizontaux. Par exemple dans la basse troposphère, la combinaison d'un cisaillement de vent et d'un mélange vertical turbulent produit une dispersion horizontale des espèces traces extrêmement efficace. Tant que les mailles horizontales sont assez grossières, il est probable de plus que la diffusion numérique soit supérieure à la diffusion latérale réelle de l'atmosphère. Enfin, il faut noter que la théorie physique qui permet d'estimer la diffusivité latérale effective est loin d'être établie.
Cependant, il est probable que, notamment pour une grille zoomée très fine,
il commence à être nécessaire d'inclure une paramétrisation de cette diffusion
latérale. Ici, cette diffusion est plutôt introduite pour des tests
de sensibilité et on retiendra une approche simple en longueur de mélange :
comme pour la super-viscosité verticale, le flux horizontal de traceur
est relié au gradient local de la quantité. L'effet de cette diffusion latérale
sur le transport des traceurs s'écrit alors sous la forme d'un laplacien
| (2.74) |
D'un point de vue informatique, l'introduction de la composante traceurs suit l'organisation du modèle LMDZ avec séparation entre dynamique et physique. Les schémas d'advection grande échelle sont interfacés avec le code dynamique. Les flux de masse aux bords des mailles sont en général cumulés dans le temps puisque les schémas d'advection admettent un pas de temps plus long que le code dynamique.
Les parties turbulentes et convectives sont gérées par un moniteur de la ``physique traceurs" interfacé avec la ``physique". Ici, on utilise en général le même pas de temps d'une demi-heure que pour la physique. C'est au niveau de ce moniteur que l'on branche les codes chimiques comme INCA développé par Hauglustaine (2004).
L'organisation de cet outil est résumée sur la Fig. 2.12.
Ce modèle est destiné avant tout a des études climatiques couplées dans lesquelles les distributions d'espèces chimiques ou d'aérosols rétroagissent sur les variables météorologiques. Cependant, notamment pour le développement et la validation, il est intéressant de disposer de versions ``débranchées" du modèle et de pouvoir forcer la situation météorologique a suivre au plus près les analyses.
Le modèle a donc été conçu de façon à pouvoir débrancher la météorologie. Les interfaces entre les parties météorologiques et traceurs ont été clairement identifiées. En mode ``branché", on passe à chaque pas de temps les flux de masse pour le transport grande échelle ou les coefficients de mélange turbulent pour la partie physique. On peut également stoker ces variables d'interface sur des fichiers (en pratique, on est obligé de les cumuler sur quelques heures) qui peuvent alors être relus pour effectuer à moindre coût des simulations de transport débranchées.
Sous réserve de cumuler proprement les champs et d'effectuer un découpage propre dans les simulations débranchées, on peut utiliser des pas de temps de quelques heures pour le stockage. Ce point a été documenté en détail par Idelkadi (2002).
Le mode débranché permet de travailler de façon un peu plus souple quand on s'intéresse à des développements spécifiques à la chimie par exemple, ou de faire des tests de sensibilité en utilisant les même champs météorologiques. Il devient surtout essentiel quand on intègre la dispersion à rebours dans le temps suivant l'approche détaillée dans le Chapitre 4.
LMDZT, en mode débranché et guidé par les analyses, s'apparente finalement à un modèle de type ``transport-chimie" (Chemistry Transport Models en anglais). Mais, alors que dans les modèles de transport-chimie la météorologie est en général directement issue des réanalyses, on effectue ici une première simulation météorologique guidée. Cette approche offre l'avantage de pouvoir extraire des paramétrisations physiques du modèle tous les paramètres jugés nécessaires pour le transport des espèces traces.
Remarquons enfin
que cette version débranchée permet éventuellement de calculer le
transport sur une grille plus fine que la grille météorologique.
Cette approche est mise en ![]() uvre dans LMDZT en redécoupant
par exemple chaque maille en 4 sous-mailles horizontalement.
uvre dans LMDZT en redécoupant
par exemple chaque maille en 4 sous-mailles horizontalement.
On montre ici deux exemples de validation du modèle LMDZT en version guidée. Dans la première application, on s'intéresse à l'isotope 222 du Radon, un radio-élément émis par les surface continentales. Ce traceur a été beaucoup utilisé pour valider et inter-comparer les codes de grande échelle. Le second exemple concerne un cas de dispersion d'une source ponctuelle, dans le cadre de la campagne européenne ETEX. On utilise une grille zoomée pour ce cas.
|
|
L'isotope 222 du Radon (![]() Rn) est un gaz trace radioactif particulièrement
adapté à la validation des modèles de transport aux échelles temporelles
de quelques heures à quelques semaines (Jacob et Prather, 1990).
Il est formé à partir de la décomposition radioactive de l'isotope 238 de
l'uranium, présent dans les sols. Les sources océaniques sont de ce fait
de deux à trois ordres de grandeur plus faibles que les sources continentales.
On peut donc voir le
Rn) est un gaz trace radioactif particulièrement
adapté à la validation des modèles de transport aux échelles temporelles
de quelques heures à quelques semaines (Jacob et Prather, 1990).
Il est formé à partir de la décomposition radioactive de l'isotope 238 de
l'uranium, présent dans les sols. Les sources océaniques sont de ce fait
de deux à trois ordres de grandeur plus faibles que les sources continentales.
On peut donc voir le ![]() Rn comme un traceur de l'air continental.
Le seul puits significatif du
Rn comme un traceur de l'air continental.
Le seul puits significatif du ![]() Rn est sa décomposition en Polonium-218 avec
une période de décroissance de 5,5 jours.
Rn est sa décomposition en Polonium-218 avec
une période de décroissance de 5,5 jours.
Le ![]() Rn a été largement utilisé pour des validations et inter-comparaisons
de modèles de transport en supposant une source uniforme sur les continents.
Ici, on utilise une version un peu plus sophistiquée, développée
par Christophe Genthon (LGGE) et Alexandre Armengaud (Genthon, 1995)
dans laquelle le
Rn a été largement utilisé pour des validations et inter-comparaisons
de modèles de transport en supposant une source uniforme sur les continents.
Ici, on utilise une version un peu plus sophistiquée, développée
par Christophe Genthon (LGGE) et Alexandre Armengaud (Genthon, 1995)
dans laquelle le ![]() Rn diffuse vers la surface
à travers une couche de sol poreuse. C'est alors le flux
en bas de cette couche qui est prescrit.
Rn diffuse vers la surface
à travers une couche de sol poreuse. C'est alors le flux
en bas de cette couche qui est prescrit.
Nous présentons une simulation guidée du ![]() Rn pour l'année 2000
avec une résolution horizontale de 2 degrés par 2 degrés.
On compare les valeurs observées et simulées à deux stations d'observation :
l'île d'Amsterdam dans l'océan indien austral (Fig. 2.13)
et Mace Head à l'extrémité occidentale de l'Irlande (Fig. 2.14).
Les deux jeux de données nous ont été aimablement communiqués par
Michel Ramonet et Philippe Ciais (LSCE).
Rn pour l'année 2000
avec une résolution horizontale de 2 degrés par 2 degrés.
On compare les valeurs observées et simulées à deux stations d'observation :
l'île d'Amsterdam dans l'océan indien austral (Fig. 2.13)
et Mace Head à l'extrémité occidentale de l'Irlande (Fig. 2.14).
Les deux jeux de données nous ont été aimablement communiqués par
Michel Ramonet et Philippe Ciais (LSCE).
Ces deux stations sont sous forte influence océanique et font donc apparaître des contrastes marqués entre un fond relativement faible et des bouffées de Radon associées à des arrivées d'air continental, soit en situation de vent d'Est sur l'Europe pour Mace Head soit quand la circulation amène sur l'île d'Amsterdam des masses d'air en provenance d'Afrique du Sud.
On voit que le modèle reproduit assez bien à la fois les valeurs faibles dans les périodes sous influence océanique et une bonne partie des pics. Des simulations pour les années 1991 et 1992 (non montrées) ont été comparées aux résultats publiés par Mahowald et al. (1997). Cette comparaison montre que le modèle se comporte raisonnablement et qu'une partie des pics non simulés provient d'erreurs sur les champs de vents analysés. Noter que la forte dépendance de la source au contenu en eau des sols est négligée ici. Elle pourrait expliquer les surestimations systématiques observées à Mace Head du 15 mai au 10 juin ou fin septembre.
Nous présentons dans cette section quelques résultats d'un travail effectué par Abderrahmane Idelkadi durant sa thèse (Idelkadi, 2002) concernant l'évaluation du modèle LMDZT en se basant notamment sur la comparaison à une série de modèles de dispersion ayant participé à la campagne ETEX (Van Dop et Nodop, 1998). La comparaison est faite par rapport à des résultats publiés il y a quelques années de cela et il est donc possible que certains de ces modèles possèdent aujourd'hui des versions plus récentes et plus performantes.
Pour cette évaluation, nous utilisons les résultats de la campagne ETEX (European Tracer EXperiment) organisée en 1994 par l'organisation mondiale de la météorologie, la Commission Européenne et l'Agence Internationale de l'Energie Atomique. Une quantité totale de 340 kg d'un gaz insoluble, le PMCH (Perfluoro-Methyl-Cyclo-Hexane), a été émise le 23 octobre 1994, à partir de 16h00 UTC (T0) et durant 12 heures, à travers une cheminée de 8 m située à Monterfil près de Rennes. Les conditions météorologiques ont été choisies de manière à ce que le traceur soit vu par le plus grand nombre possible des 168 stations d'observation réparties sur l'Europe. L'expérience a duré trois jours et les mesures de concentration du polluant ont été effectuées toute les trois heures à chaque station.
![$\includegraphics[height=15cm,angle=-90]{lmdzt/FIGURES/grille.eps}$](img359.png)
|
La Fig. 2.15 montre la grille LMDZ choisie pour la simulation avec un zoom sur l'Europe. On montre aussi en incrustation l'emplacement de 11 stations privilégiées par les organisateurs pour certains diagnostics lors des études d'intercomparaison.
|
La Fig. 2.16 montre les panaches observés et simulés à différents
instants.
On voit que le panache est globalement bien reproduit, à la fois en
répartition spatiale et en intensité.
Pour quantifier cet accord, on utilise l'un des critères statistiques
retenus pour l'intercomparaison des modèles dans le cadre d'ETEX.
Il s'agit du FMT pour Figure of Merit in Time.
Le FMT se définit comme le rapport (traduit en pourcentage)
![\includegraphics[height=4.5cm]{lmdzt/FIGURES/fmt2.eps}](img367.png)
![\includegraphics[height=11cm]{lmdzt/FIGURES/interc.eps}](img368.png)
|
La Fig. 2.17 montre les FMTs obtenus pour les 11 stations montrées sur la Fig. 2.15. Ces FMTs sont comparés à ceux obtenus avec une trentaine d'autres modèles. Les conclusions des inter-comparaisons ETEX avaient identifié une poignée de modèles qui se plaçaient au dessus du lot. Les performances relatives des différents modèles semblaient d'ailleurs peu liées à leurs caractéristiques, que ce soit au type d'approche (lagrangienne ou eulérienne par exemple) ou aux résolutions spatiales retenues. Il est fort probable d'ailleurs que les meilleurs modèles étaient en grande partie limités par le caractère imparfait des analyses météorologiques. Le modèle LMDZT n'a rien d'exceptionnel mais fait partie de ces bons modèles.
![\includegraphics[height=7cm]{lmdzt/FIGURES/mod_resolution.epsi}](img369.png)
![\includegraphics[height=6cm]{lmdzt/FIGURES/redecoupage.eps}](img370.png)
|
Les cartes suggèrent que le modèle est un peu trop diffusif. Les panaches à 24 et 48 heures sont en particulier plus étendus que les panaches observés. Des tests de sensibilité à la résolution (Fig. 2.18) indiquent que, quand on raffine la grille d'un facteur 2 dans les deux directions horizontales, on diminue la diffusion horizontale, mais en réduisant plutôt l'accord avec les mesures. A partir d'une maille de quelques dizaines de kilomètres, le modèle semble donc sous-estimer la diffusion horizontale. Ces résultats sont présentés plus en détail par Idelkadi (2002).
On voit que le code LMDZT peut être utilisé comme un code de dispersion atmosphérique. Mais LMDZT se distingue par de nombreux aspects des codes développés spécifiquement pour les calculs de dispersion.
D'abord, un certain nombre de ces codes sont bâtis sur des trajectoires particulaires ou Lagrangiennes. Cette approche semble relativement intuitive quand on a une source ponctuelle comme celle d'ETEX. Cependant, elle pose le problème que plus la dispersion devient importante, et plus le nombre de particules à injecter est grand si on veut pouvoir prédire les concentrations faibles observées loin des sources. Le traitement du transport turbulent est aussi une difficulté des codes particulaires. Certains font simplement l'impasse. D'autres utilisent des approches de type marche aléatoire. Par exemple, Vautard et al. (2001) commencent par estimer la hauteur de la couche limite puis déplacent aléatoirement les particules au sein de cette couche limite. On voit qu'il faut à nouveau ajouter un grand nombre de particule pour obtenir un traitement statistique correct de ce phénomène. Les codes eulériens bénéficient pour leur part des nombreux efforts de recherche développés dans les modèles météorologiques.
Le modèle LMDZT se distingue aussi des modèles de transport-chimie comme on l'a vu, en ce sens qu'il calcule sa propre météorologie. Pour la recherche climatique, les motivations pour cette approche sont claires. Le but ultime est de prendre en compte, de façon interactive, les rétroactions des espèces transportées sur la météorologie. Dans ce cadre, les versions guidées et débranchées du modèle ne sont qu'un mode particulier d'utilisation permettant la validation sur des campagnes d'observation. L'avantage potentiel pour simuler la dispersion dans un contexte de surveillance de l'environnement est plus subtile. Dans les modèles de transport classiques, des phénomènes physiques comme le mélange turbulent dans la couche limite ou le lessivage par les pluies doivent être calculés d'une façon ou d'une autre. Il faut alors essayer de diagnostiquer, à partir de champs météorologiques incomplets (disponibles toutes les 6 heures seulement par exemple), des coefficients de mélange turbulents ou des taux de précipitation dans l'atmosphère. Dans l'approche retenue ici, on effectue une simulation météorologique complète, dans laquelle ces différents aspects sont représentés, tout en guidant la simulation pour qu'elle colle au plus près aux champs de vents de grande échelle issus des analyses. A noter que pour répondre à la même préoccupation, les centres qui produisent les analyses et réanalyses météorologiques se sont mis petit à petit à archiver pour les modèles de transport-chimie des variables internes des paramétrisations comme les coefficients de diffusion turbulente ou les flux de masse convectifs.
Enfin, le modèle LMDZT se distingue des modèles régionaux par l'utilisation d'une grille globale à maille variable. Pour des applications où on utilise des observations réparties uniformément sur le globe, comme dans le cas du TICE exposé dans le Chapitre 4, le modèle global s'impose naturellement. Dans le cas d'évènements relativement localisés, les modèles à domaine limité présentent un meilleur rapport précision/coût. Cependant, même pour une source ponctuelle, le modèle global est intéressant en ce sens qu'on n'a pas à se poser à l'avance le problème du choix du domaine. Le zoom est effectué sur le point source. Tant que le panache est proche de la source, et donc relativement concentré, le calcul est très précis. Plus on s'éloigne de cette source et moins le calcul est précis. Mais cette perte de précision a aussi moins d'importance puisque le panache est de toutes façons beaucoup plus diffus.
Cette remarque s'applique de la même façon pour les rétro-simulations (cf. Chapitre 4). Si on interprète une mesure à une station, par exemple la mesure d'une concentration élevée d'un polluant suggérant un accident industriel, une rétro-simulation à partir de la station avec un zoom aux abords de cette station permettra de bien décrire l'origine de l'air, à la fois finement près de la station mais également à l'autre bout du globe. Il ne sera donc pas nécessaire de faire des hypothèses a priori sur l'origine de la pollution.
Les développements présentés plus haut et mis en musique dans le modèle LMDZ sont impliqués dans un grand nombre d'études dont les plus importantes sont brièvement décrites ci-dessous.
Au LOA, Olivier Boucher a été à l'origine d'une partie des développements concernant l'introduction de la composante traceurs dans LMDZ (notamment pour ce qui est du transport convectif). Il a depuis introduit dans LMDZ une représentation en ligne du cycle du soufre. Cette version contient 7 traceurs advectés (DMS, 2, H2S, DMSO, MSA, sulfates et 2O2). Les principaux oxydants (OH, 2, 3 et Ø3) sont pour leur part prescrits. Cette version du modèle a notamment été utilisée pour évaluer l'évolution entre l'époque pré-industrielle et l'époque actuelle du forçage radiatif des aérosol soufrés (Boucher, 2002). Une part importante de la problématique concerne l'évaluation de l'effet indirect de ces aérosols (Quaas et al., 2004) au travers des changements des propriétés microphysiques des nuages : diminution de la taille et augmentation du nombre des gouttes d'eau (premier effet indirect) à cause du nombre accru de noyaux de condensation en cas d'augmentation des aérosols, entraînant également une précipitation moindre et une durée de vie accrue des nuages (second effet indirect). Cette version a été récemment étendue aux autres composantes de l'aérosol et validée par rapport aux résultats de la campagne INDOEX (Reddy et al., 2004). Cette version avec aérosols a également été utilisée pour prédire la possible rétroaction d'un réchauffement climatique sur les aérosols naturels : notamment sur les sulfates à cause de la modification des DMS marins (Boucher et al., 2003; Bopp et al., 2004) mais aussi pour les sels marins et les aérosols désertiques, dont l'émission est sensible aux vents en surface.
Cette version du modèle avec cycle du soufre a récemment été adaptée aux hautes latitudes par l'équipe de Christophe Genthon au LGGE (Cosme et al., 2002) en vue notamment de l'interprétation des reconstitutions historiques effectuées à partir des calottes de glace (voir aussi Krinner et Genthon, 2003).
Plus récemment, Didier Hauglustaine a développé pour LMDZ un module de chimie et aérosols interactifs, INCA. Les développements et études menés avec LMDZ-INCA se sont principalement portés sur une version 4-NOx-Ø3 troposphérique, visant principalement a étudier les gaz à effet de serre autres que le 2. Un très important travail de validation a été réalisé sur cette version dans laquelle une quarantaine d'espèces sont advectées (Hauglustaine, 2004).
Cette version a été utilisée pour évaluer l'impact radiatif d'un changement des émissions de CO et des NOx via la modification de la distribution de l'ozone et des radicaux OH. Le modèle a également été utilisé pour étudier l'impact des émissions liées aux transport aérien sur la composition chimique de l'atmosphère et sur le climat.
Le modèle a également été couplé au module REPROBUS développé par Franck Lefèvre pour la chimie stratosphérique.
La version martienne du modèle LMDZ (Hourdin et al., 1995a,1993) s'est enrichie au fil des années. Les poussières, dont l'impact radiatif est très important même en dehors des grandes tempêtes de poussières globales, ont tout d'abord été incluse. Puis le cycle de l'eau (Montmessin, 2004), très important pour essayer de contraindre les réservoirs d'eau actuels et attaquer les questions relatives aux climats passés de Mars. Une composante chimique a également été inclue dans le modèle, tout d'abord pour étendre le modèle jusqu'à la thermosphère dans le cadre du développement d'une base de données atmosphérique martienne pour l'ASE et le CNES (Angelats i Coll, 2004), puis, plus récemment avec le développement d'un module de chimie pour la basse atmosphère (0 à 120 km) (Lefèvre, 2004).
La version traceurs de LMDZ est également utilisée dans deux grands types d'applications qui font l'objet de deux chapitres spécifiques du présent document et ne sont donc que mentionnés ici.
Le modèle est d'abord utilisé en mode rétro-transport (Chapitre 4) dans deux cadres principalement : l'inversion des puits et sources de 2 et la détection des essais nucléaires.
Le modèle a également été beaucoup utilisé pour l'étude des couplages entre dynamique atmosphérique, chimie et microphysique des brumes dans l'atmosphère de Titan (Chapitre 5). A noter qu'une version vénusienne du modèle est actuellement en cours de développement.
![\includegraphics[width=16cm]{lmdzt/FIGURES/RN/rnconv.eps}](img371.png) |
Un travail a été effectué récemment par Marie-Angèle Filiberti et Jean-Yves Grandpeix pour introduire la composante traceurs dans le schéma convectif d'Emanuel. D'un point de vue du transport, la différence principale entre le schéma d'Emanuel et celui de Tiedtke est la possibilité pour une parcelle d'air sortant de l'ascendance convective à un certain niveau d'être détraînée dans l'environnement à n'importe quel niveau du modèle. La fermeture (permettant de calculer le flux à la base de la colonne convective en fonction d'autres paramètres du modèle de circulation) est également très différente et la convection pénètre généralement plus haut avec le schéma d'Emanuel. On n'entre pas ici dans les détails de la formulation mais on illustre simplement sur la Fig. 2.19 l'importance de la représentation du transport convectif pour le transport des traceurs.
La figure montre, pour un mois de janvier et en moyenne zonale, la structure
méridienne de la concentration de ![]() Rn obtenue
avec le schéma de Tiedtke (en haut), avec celui d'Emanuel (au milieu)
et la différence relative.
Dans la région de convergence intertropicale, localisée principalement
sur l'Afrique, l'Amérique du sud et l'Indonésie à cette saison,
entre 30S et l'équateur, le Radon est détraîné beaucoup plus haut
en altitude avec le schéma d'Emanuel et beaucoup moins dans la troposphère
moyenne.
Aux autres latitudes, l'effet du schéma d'advection est sans doute moins
directe.
Les concentrations de Radon peuvent notamment être affectées par des
variations de la circulation à grande échelle.
On n'entre pas ici dans ces considérations.
Rn obtenue
avec le schéma de Tiedtke (en haut), avec celui d'Emanuel (au milieu)
et la différence relative.
Dans la région de convergence intertropicale, localisée principalement
sur l'Afrique, l'Amérique du sud et l'Indonésie à cette saison,
entre 30S et l'équateur, le Radon est détraîné beaucoup plus haut
en altitude avec le schéma d'Emanuel et beaucoup moins dans la troposphère
moyenne.
Aux autres latitudes, l'effet du schéma d'advection est sans doute moins
directe.
Les concentrations de Radon peuvent notamment être affectées par des
variations de la circulation à grande échelle.
On n'entre pas ici dans ces considérations.
Cette grande sensibilité au transport atmosphérique pourrait laisser penser que
les traceurs peuvent fournir une contrainte forte sur la
représentation du transport, et notamment la convection.
Le ![]() Rn a d'ailleurs été beaucoup utilisé pour des inter-comparaisons
de modèles globaux (cf. par exemple, Jacob et Prather, 1990; Jacob, 1997).
Malheureusement, même avec les différences très importantes obtenues
ici, les observations de la concentration restent souvent insuffisantes
pour valider réellement les modèles et choisir entre deux paramétrisations.
Des campagnes dédiées, comme la campagne AMMA d'Analyse Multi-échelles
de la Mousson Africaine, avec déploiement d'instruments aéroportés
autour des systèmes convectifs combinant détection passive et active
et mesures météorologiques et chimiques devraient permettre d'avancer
sur ce point.
Rn a d'ailleurs été beaucoup utilisé pour des inter-comparaisons
de modèles globaux (cf. par exemple, Jacob et Prather, 1990; Jacob, 1997).
Malheureusement, même avec les différences très importantes obtenues
ici, les observations de la concentration restent souvent insuffisantes
pour valider réellement les modèles et choisir entre deux paramétrisations.
Des campagnes dédiées, comme la campagne AMMA d'Analyse Multi-échelles
de la Mousson Africaine, avec déploiement d'instruments aéroportés
autour des systèmes convectifs combinant détection passive et active
et mesures météorologiques et chimiques devraient permettre d'avancer
sur ce point.
On peut bien sûr envisager d'utiliser, pour les variables météorologiques
du modèle de circulation générale, les schémas en volumes finis introduits
dans le modèle pour transporter les espèces traces. C'est en fait
déjà le cas pour la vapeur d'eau dont l'advection est maintenant
calculée dans la
version standard du modèle avec le schéma I de Van Leer.
L'advection de l'eau et de la température potentielle étaient
déjà de fait écrites dans la version originale du modèle comme des schémas en volumes
finis, avec un flux calculé simplement comme le produit du flux de masse
par une interpolation linéaire de la quantité transportée à l'interface :
Ce qui est moins direct, c'est de remarquer que la propriété de conservation de l'enstrophie, importante pour la stabilité du modèle et pour la bonne représentation des transferts entre échelles pour les écoulements stratifiés (Sadourny, 1975a,b), découle en fait d'une formulation volumes finis cachée de l'advection de la vorticité. Cette remarque permet d'envisager une réécriture complète du code dynamique, proche de l'esprit actuel, mais dans laquelle on remplacerait les schémas d'advection par des schémas en volumes finis présentant de meilleurs propriétés physiques comme le schéma I de Van Leer ou PPM.
En introduisant
le facteur de Coriolis multiplié par l'aire de la maille,
![]() où
où ![]() est la vitesse de rotation de la planète,
ainsi que la vorticité potentielle absolue
est la vitesse de rotation de la planète,
ainsi que la vorticité potentielle absolue
| (2.78) |
| (2.79) |
Les termes d'advection verticale de ![]() et
et ![]() , respectivement
, respectivement
![]() et
et ![]() , ont été modifiés dans le passé pour
garantir partiellement la conservation du moment cinétique par le modèle
(Hourdin, 1992).
Les formulations originales
non conservatives et conservatives de ces termes sont données
dans la Table 2.1.
, ont été modifiés dans le passé pour
garantir partiellement la conservation du moment cinétique par le modèle
(Hourdin, 1992).
Les formulations originales
non conservatives et conservatives de ces termes sont données
dans la Table 2.1.
En fait, Robert Sadourny (communication personnelle)
avait remarqué fort justement que la conservation du moment cinétique
était également garantie si la double moyenne
en ![]() sur le terme en
sur le terme en ![]() était appliquée plutôt à
était appliquée plutôt à ![]() , ce
qui conduisait à lisser le champ de vitesse verticale pour l'advection
verticale.
En faisant cette transformation, on peut revenir à la forme originelle avec une
triple moyenne sur les champs de vitesse verticale (formulation 2 dans
la table) ce qui est plus sympathique. En pratique, on peut commencer par
calculer
, ce
qui conduisait à lisser le champ de vitesse verticale pour l'advection
verticale.
En faisant cette transformation, on peut revenir à la forme originelle avec une
triple moyenne sur les champs de vitesse verticale (formulation 2 dans
la table) ce qui est plus sympathique. En pratique, on peut commencer par
calculer
![]() avant la moyenne.
Cette formulation 2 peut facilement être testée dans le modèle actuel.
avant la moyenne.
Cette formulation 2 peut facilement être testée dans le modèle actuel.
|
On réalise en fait facilement que l'astuce principale
du schéma original de Sadourny,
conservatif en enstrophie, a consisté à récrire la partie vorticité
de l'équation du mouvement sous la forme d'un flux de vorticité.
En effet,
avec les notations ci-dessus, la version numérique de l'équation de bilan
de vorticité s'écrit :
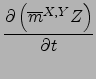 |
![$\displaystyle \frac{\partial {\cal F}\left[ \delta_x \tilde{v}- \delta_y \tilde{u} \right]}{\partial t}$](img395.png) |
(2.82) | |
![$\displaystyle {\cal F}\left[ \delta_x \frac{\partial \tilde{v}}{\partial t}-\delta_y \frac{\partial \tilde{v}}{\partial t} \right]$](img396.png) |
(2.83) | ||
| (2.84) | |||
![\includegraphics[width=15cm]{lmdzt/FIGURES/grilles.eps}](img399.png) |
Pour des écoulements barotropes (![]() et
et
![]() ), on obtient
une équation de bilan
), on obtient
une équation de bilan
![$\displaystyle \frac{\partial \left({\overline{m}}^{ X,Y } Z\right)}{\partial t}...
...ht)+\delta_y \left({\overline{Z}}^{ Y } {\overline{V}}^{ X,Y }\right) \right]=0$](img404.png) |
(2.85) |
La figure 2.20 illustre le positionnement des variables dans la formulation actuelle si on les interprète en termes de volumes finis.
Il est donc tentant, de la même façon que pour les traceurs, ou la température potentielle, de remplacer les moyennes arithmétiques par des estimations amont à la Van Leer.
On n'obtiendra plus alors, comme dans l'ancien modèle, une conservation exacte de l'enstrophie. En revanche, en appliquant un schéma positif, monotone, etc ... on empêchera la création d'extrema numérique du champ de vorticité. On obtiendra également automatiquement de la dissipation à l'échelle de la maille en présence d'un extremum de vorticité important.
On peut essayer d'appliquer directement une formulation volumes finis aux équations ci-dessus. Il y a un petit problème pratique : les schémas volumes finis utilisés pour la vorticité et la température potentielle travailleront sur des grilles décalées.
Cependant, on se rend compte qu'en décalant les variables scalaires sur la grille des points de vorticité, on obtient une écriture plus systématique.
Dans la nouvelle configuration, la position des points ![]() et
et ![]() ,
des points de vorticité et des flux de masse utilisés pour l'advection est
inchangée.
Mais, les scalaires doivent être advectés, comme la vorticité, avec les flux de masse moyens en
,
des points de vorticité et des flux de masse utilisés pour l'advection est
inchangée.
Mais, les scalaires doivent être advectés, comme la vorticité, avec les flux de masse moyens en ![]() et en
et en ![]() .
.
Il est en fait plus clair de redéfinir les variables ![]() et
et ![]() comme des
doubles moyennes des flux de masse obtenus à partir de
comme des
doubles moyennes des flux de masse obtenus à partir de
![]() et
et
![]() :
:
| (2.86) |
| (2.87) |
L'équation de continuité s'écrit alors formellement comme précédemment
La pression de surface est encore la somme verticale de la masse
La vorticité potentielle absolue devient
| (2.90) |
Pour l'énergie cinétique,
on a le choix entre la calculer comme avant sur l'ancienne grille scalaire,
| (2.91) |
| (2.92) |
Les équations du mouvement prennent finalement la forme suivante:
| (2.95) |
Pour le terme d'advection verticale, on utilise ici l'équivalent de la
version "conservation 2" puisque les flux de masses horizontaux (et donc
le flux de masse vertical) sont déjà moyennés
dans les deux directions horizontales.
De ce fait,
![]() dans la nouvelle formulation
correspond à
dans la nouvelle formulation
correspond à
![]() dans l'ancienne.
Il est intéressant de remarquer que le choix original de la forme non
conservative était le choix le plus ``naturel" et que des modifications
avaient dû être introduites après coup pour garantir la conservation du
moment cinétique zonal.
Ici, le choix ``naturel" correspond au choix conservatif.
dans l'ancienne.
Il est intéressant de remarquer que le choix original de la forme non
conservative était le choix le plus ``naturel" et que des modifications
avaient dû être introduites après coup pour garantir la conservation du
moment cinétique zonal.
Ici, le choix ``naturel" correspond au choix conservatif.
Une maquette de cette nouvelle formulation a été développée par Phu LeVan sur une grille longitude-latitude. Elle est actuellement en cours de test. Si cette approche s'avère efficace et robuste, elle pourrait donner une excellente base pour développer une dynamique icosaédrique, 2.17vieux rêve rentré de Robert Sadourny, qui hante encore les étagères de certains collègues au laboratoire.
Le transport turbulent dans la couche limite est essentiel
à la fois bien sûr pour la météorologie et le climat, mais également
pour toutes les espèces traces ayant des sources et puits en surface
(vapeur d'eau, CO![]() , espèces chimiques et aérosols de pollution,
aérosols désertiques).
Les évolutions récentes des paramétrisations des modèles de climat
se sont portées davantage sur la représentation de la convection
nuageuse profonde que sur la couche limite.
Pour modéliser la convection nuageuse, les modèles récents
utilisent en particulier souvent
des schémas dits "en flux de masse" dans lesquels on
explicite des flux ascendants, souvent intenses et concentrés, des
descentes également concentrées associées aux précipitations, et des
flux compensatoires plus lents dans l'environnement.
, espèces chimiques et aérosols de pollution,
aérosols désertiques).
Les évolutions récentes des paramétrisations des modèles de climat
se sont portées davantage sur la représentation de la convection
nuageuse profonde que sur la couche limite.
Pour modéliser la convection nuageuse, les modèles récents
utilisent en particulier souvent
des schémas dits "en flux de masse" dans lesquels on
explicite des flux ascendants, souvent intenses et concentrés, des
descentes également concentrées associées aux précipitations, et des
flux compensatoires plus lents dans l'environnement.
Comparativement, les paramétrisations utilisées dans les modèles grande échelle
pour la couche limite restent souvent rudimentaires.
Elles sont la plupart du temps basées sur des adaptations de formulations
locales. On entend par là que le flux vertical turbulent d'une quantité ![]() ne
dépend que des caractéristiques locales de l'écoulement.
Cette approche locale s'appuie sur une analogie avec la diffusion moléculaire,
les mouvements turbulents aléatoires jouant le
rôle des mouvements browniens des molécules pour la diffusion moléculaire.
Ce flux s'exprime alors comme le produit du gradient local de
ne
dépend que des caractéristiques locales de l'écoulement.
Cette approche locale s'appuie sur une analogie avec la diffusion moléculaire,
les mouvements turbulents aléatoires jouant le
rôle des mouvements browniens des molécules pour la diffusion moléculaire.
Ce flux s'exprime alors comme le produit du gradient local de ![]() par un coefficient de mélange turbulent ne dépendant lui-même que des
conditions météorologiques locales. On parle de diffusion
turbulente ou super-viscosité.
On sait depuis longtemps que cette vision diffuse de la turbulence
ne permet pas de rendre
compte d'un certain nombre de phénomènes atmosphériques et notamment du
transport de chaleur en remontant le gradient (du froid vers le chaud
en termes de température potentielle)
très souvent observé dans la couche limite convective.
Ce transport à contre-gradient est effectué en fait par des structures
organisées méso-échelles qui emmènent directement l'air
chaud de la couche de surface vers le haut de la couche limite.
Ce sont ces structures - thermiques, pompes, rouleaux convectifs - qui
font la joie des pilotes de planeurs et autres engins volants.
par un coefficient de mélange turbulent ne dépendant lui-même que des
conditions météorologiques locales. On parle de diffusion
turbulente ou super-viscosité.
On sait depuis longtemps que cette vision diffuse de la turbulence
ne permet pas de rendre
compte d'un certain nombre de phénomènes atmosphériques et notamment du
transport de chaleur en remontant le gradient (du froid vers le chaud
en termes de température potentielle)
très souvent observé dans la couche limite convective.
Ce transport à contre-gradient est effectué en fait par des structures
organisées méso-échelles qui emmènent directement l'air
chaud de la couche de surface vers le haut de la couche limite.
Ce sont ces structures - thermiques, pompes, rouleaux convectifs - qui
font la joie des pilotes de planeurs et autres engins volants.
Depuis longtemps, cette difficulté est contournée dans les modèles de
circulation générale en utilisant un "contre-gradient" (Deardorff, 1972b):
au lieu d'utiliser directement le gradient vertical de la température
potentielle
![]() dans le calcul du flux de chaleur,
on soustrait à ce gradient une valeur qui
permet d'avoir un flux de chaleur vers le haut, même dans une atmosphère
légèrement stable.
Des développements récents (Troen et Mahrt, 1986; Abdella et McFarlane, 1997; Holtslag et Boville, 1993)
on permis de dériver des expressions moins arbitraires pour le contre-gradient,
en prenant en compte indirectement l'existence de ces structures méso-échelles.
Ces formulations permettent également d'introduire cette composante
non-locale pour le transport des espèces traces ce qui n'étaient pas
le cas dans la version originale de Deardorff (1972b).
dans le calcul du flux de chaleur,
on soustrait à ce gradient une valeur qui
permet d'avoir un flux de chaleur vers le haut, même dans une atmosphère
légèrement stable.
Des développements récents (Troen et Mahrt, 1986; Abdella et McFarlane, 1997; Holtslag et Boville, 1993)
on permis de dériver des expressions moins arbitraires pour le contre-gradient,
en prenant en compte indirectement l'existence de ces structures méso-échelles.
Ces formulations permettent également d'introduire cette composante
non-locale pour le transport des espèces traces ce qui n'étaient pas
le cas dans la version originale de Deardorff (1972b).
Stull (1984) avait souligné l'importance des aspects non locaux du transport vertical dans la couche limite et proposé un formalisme général basé sur des matrices d'échange (baptisées matrices de ``transilience'') pour traiter ce problème dans les modèles numériques, afin de rompre de façon radicale d'avec la diffusion turbulente. Sur la base des matrices de transiliences, Pleim et Chang (1992) ont proposé un ``modèle de convection asymétrique" basé sur l'image d'un transport par une ascendance concentrée et une subsidence compensatoire lente. Le caractère non local verticalement du mélange, et la dissymétrie entre ascendances convectives concentrées (et descentes précipitantes pour les cumulo-nimbus et congénères) et subsidences compensatoires sont à la base des schémas dit ``en flux de masse" (Arakawa et Schubert, 1974; Emanuel, 1991; Tiedtke, 1989) qui se sont largement répandus dans les modèles de circulation générale. Ces idées de modèles ``en flux de masse" ont également été appliquées pour la couche limite convective (notamment pour les cumulus d'alizés) mais en utilisant généralement des modèles dits de "couche mélangée" (``mixed layer formulation'' ou aussi ``bulk models'' en anglais).
Le "modèle du thermique" proposé ici s'inspire plus directement des modèles de la convection nuageuse, en reprenant notamment, comme dans le schéma d'Emanuel, l'idée d'un panache ascendant non mélangé, épluché progressivement au cours de son ascendance. Sans entrer dans le détail, on détermine pour chaque couche instable (surmontée par de l'air plus froid en termes de température potentielle virtuelle), un profil vertical de vitesse ascendante à partir de la flottabilité d'une parcelle d'air entraînée depuis cette couche en conservant sa température potentielle. Ces calculs sont ensuite utilisés pour décrire une ascendance (le thermique) alimentée en air par les couches instables près de la surface, et compensée par une subsidence plus lente dans l'environnement. Ce schéma tient compte de la structure géométrique de ces cellules convectives, notamment pour relier vitesses verticales et flux de masse.
Le modèle du thermique n'est pas un modèle de couche limite complet. Il ne représente que la partie meso-échelle de la dynamique de la couche limite. On conserve dans le modèle de circulation générale, en parallèle du modèle du thermique, une formulation en diffusion turbulente, active notamment dans la couche limite de surface. Il faut donc considérer qu'on a rajouté dans le modèle climatique une échelle entre l'échelle turbulente et l'échelle de la convection nuageuse.
Dans ce chapitre, on revient assez largement sur les approches classiques de la paramétrisation de la couche limite (Section 3.1). On présente aussi les spécificités de la couche limite convective (Section 3.2) et les approches qui ont été proposées pour la représenter (Section 3.3). On présente ensuite en détail le modèle du thermique (Section 3.4). Ce modèle est enfin testé, aussi bien pour les aspects météorologiques - en utilisant à la fois les résultats de simulations des grands tourbillons (Section 3.5) et des mesures in-situ (Section 3.6) - que pour le transport des espèces traces (Section 3.7).
Nous avions commencé avec Richard Fournier à nous intéresser à ces questions de couche limite sur Mars (en adaptant notamment dans le modèle de circulation martien le modèle de couche limite de Mellor et Yamada). Fleur Couvreux, Camille Risi et Catherine Rio ont contribué lors de différents stages à développer, affiner ou valider la paramétrisation. Abderrahmane Idelkadi a effectué des comparaisons systématiques sur le transport du Radon. Enfin les discussions avec Alain Lahellec, Anne Mathieu et Jean-Yves Grandpeix ont beaucoup contribué au mûrissement des idées.
Comme on l'a dit plus haut, les paramétrisations en diffusion turbulente
sont construites par analogie avec la diffusion moléculaire.
Cette approche s'est révélée
particulièrement fructueuse pour expliquer certaines caractéristiques
de la couche limite atmosphérique et dériver des paramétrisations pour
les modèles de circulation atmosphérique.
Avant de parler de mise en défaut de cette théorie dans le cas des couches
limites convectives, on retrace les grandes lignes des différentes
approches en diffusion turbulente. Cette section permet également de
décrire
des paramétrisations qui sont par la suite comparées, sur des cas académiques
ou réalistes de couches limites convectives, au modèle du thermique.
On introduit les différentes formulations sous des hypothèses classiques
de couche limite qui supposent que les quantités moyennes varient
moins vite horizontalement que verticalement
(
![]() et
et
![]() où
où ![]() est la moyenne d'ensemble de
est la moyenne d'ensemble de ![]() pondérée par l'air définie
dans la Section 2.2).
pondérée par l'air définie
dans la Section 2.2).
Dans le chapitre précédent, on a introduit rapidement l'utilisation
de la diffusion turbulente pour paramétriser le transport turbulent
d'une quantité ![]() dans la couche limite
dans la couche limite
| (3.1) |
Une façon physique d'introduire cette formulation et d'estimer
le coefficient ![]() est l'approche de la longueur de mélange introduite
à l'origine par Prandtl en 1925.
L'image physique sous-tendue est l'existence de petites structures turbulentes
avec une taille caractéristique, ou longueur de mélange,
est l'approche de la longueur de mélange introduite
à l'origine par Prandtl en 1925.
L'image physique sous-tendue est l'existence de petites structures turbulentes
avec une taille caractéristique, ou longueur de mélange, ![]() .
.
En se plaçant pour fixer les idées dans une configuration où la concentration
moyenne du traceur croît verticalement (
![]() ),
un mouvement descendant sera associé
en moyenne à une fluctuation positive de
),
un mouvement descendant sera associé
en moyenne à une fluctuation positive de ![]() . La fluctuation
. La fluctuation ![]() associée
à ce mouvement turbulent sera d'autant plus grande que les contrastes verticaux
de
associée
à ce mouvement turbulent sera d'autant plus grande que les contrastes verticaux
de ![]() sont grands. En supposant que la particule qui descend a conservé
les propriétés qu'avait l'air à une distance
sont grands. En supposant que la particule qui descend a conservé
les propriétés qu'avait l'air à une distance ![]() au-dessus, et en supposant
au-dessus, et en supposant
![]() petit devant la hauteur caractéristique des variations de
petit devant la hauteur caractéristique des variations de ![]() (c'est cette dernière hypothèse qui n'est pas valide dans les
cas de couches limites convectives) on peut écrire
(c'est cette dernière hypothèse qui n'est pas valide dans les
cas de couches limites convectives) on peut écrire
| (3.2) |
| (3.3) |
Dans ce cadre, le coefficient ![]() est simplement
est simplement ![]() .
.
Si on suppose que la turbulence est isotrope (par exemple en atmosphère
neutre et loin du sol), on peut aller un cran plus loin en remarquant
qu'on a
| (3.4) |
| (3.5) |
La théorie de la diffusion turbulente a remporté un de ses plus francs succès dans l'explication de la structure de la couche limite de surface.
Près de la surface, on suppose que la longueur caractéristique
des échanges turbulents est proportionnelle à la distance à la
surface, ![]() .
En choisissant un repère local tel que
.
En choisissant un repère local tel que ![]() soit dans la
direction du vent
moyen près de la surface, et en remarquant que
soit dans la
direction du vent
moyen près de la surface, et en remarquant que ![]() (noté
(noté ![]() ci-après)
et son gradient
en
ci-après)
et son gradient
en ![]() sont du même signe près de la surface
- puisque
sont du même signe près de la surface
- puisque
![]() doit s'annuler en
doit s'annuler en ![]() -, il vient
-, il vient
| (3.6) |
Si on définit la couche de surface comme la partie de la couche limite
dans laquelle les flux turbulents ne diffèrent pas trop (par moins de 10%
par exemple) du flux en surface - c'est à dire qu'on peut écrire
![]() où
où ![]() est le module de la tension de vent en surface - on obtient
est le module de la tension de vent en surface - on obtient
| (3.7) |
Les mesures expérimentales de
la constante de Von Karman, ![]() , supposée universelle, donnent des valeurs
comprises entre 0,35 et 0,43.
, supposée universelle, donnent des valeurs
comprises entre 0,35 et 0,43.
Sous ces hypothèse, près de la surface, le vent varie de façon logarithmique
avec la verticale. La singularité en surface est résolue en supposant
que le vent s'annule non pas en ![]() mais à une altitude
mais à une altitude ![]() , appelée
longueur de rugosité, telle que
, appelée
longueur de rugosité, telle que
| (3.8) |
De la même façon, à partir du flux de chaleur sensible en surface
![]() , on peut introduire une
échelle des fluctuations turbulentes
de température potentielle,
, on peut introduire une
échelle des fluctuations turbulentes
de température potentielle,
![]() ,
reliée au gradient de température potentielle par
,
reliée au gradient de température potentielle par
| (3.9) |
| (3.10) |
La décomposition de Reynolds, qui a permis de faire apparaître des termes
croisés du type
![]() dans les équations des variables moyennes
(Section 2.2),
peut bien sûr être poussée plus loin. On écrit alors des
équations d'évolution pour les quantités turbulentes
dans les équations des variables moyennes
(Section 2.2),
peut bien sûr être poussée plus loin. On écrit alors des
équations d'évolution pour les quantités turbulentes ![]() ,
, ![]() ,
,
![]() en soustrayant la moyenne d'ensemble à l'équation complète.
On peut ainsi obtenir des équations d'évolution temporelle des
termes croisés
en soustrayant la moyenne d'ensemble à l'équation complète.
On peut ainsi obtenir des équations d'évolution temporelle des
termes croisés
![]() ,
,
![]() ,
,
![]() , ...
On peut donc imaginer des fermetures où, au lieu de spécifier directement
, ...
On peut donc imaginer des fermetures où, au lieu de spécifier directement
![]() en fonction des grandeurs moyennes (de type diffusion
turbulente),
on considère le flux turbulent lui-même comme une variable indépendante du
modèle suivant sa propre évolution. Mais ces nouvelles équations font
elles-mêmes apparaître des termes du troisième ordre.
en fonction des grandeurs moyennes (de type diffusion
turbulente),
on considère le flux turbulent lui-même comme une variable indépendante du
modèle suivant sa propre évolution. Mais ces nouvelles équations font
elles-mêmes apparaître des termes du troisième ordre.
Une littérature très savante a été consacrée à ces fermetures à des ordres plus élevés. Cette histoire, qui semble avoir commencé dans les années 50, a produit les premiers modèles utilisables comme fermetures turbulentes au début des années 70. C'est le cas notamment du travail de Mellor et Yamada (1974). Dans cette approche, la fermeture (dite d'ordre 2) s'effectue au niveau des termes du troisième ordre, en introduisant notamment une mesure de l'anisotropie de la turbulence. De façon générale, on peut calculer les termes croisés à partir d'équations pronostiques qui font apparaître trois types de termes : des termes de transport, des corrélations pression-vitesse et des termes de dissipation. On aboutit typiquement alors à une dizaine d'équations pour prédire les différents termes croisés.
Les fermetures utilisées en pratique dans les modèles atmosphériques,
comme celle de Mellor et Yamada (1974)
ou les fermetures dites ![]() , sont des versions simplifiées des
fermetures d'ordre 2 où on se focalise sur l'équation d'évolution
de l'énergie cinétique turbulente
, sont des versions simplifiées des
fermetures d'ordre 2 où on se focalise sur l'équation d'évolution
de l'énergie cinétique turbulente
| (3.11) |
En effet,
si on revient à la présentation de la longueur de mélange faite précédemment,
il est naturel de prendre ![]() comme amplitude des
mouvements turbulents verticaux
comme amplitude des
mouvements turbulents verticaux
![]() dans le cas d'une turbulence isotrope en atmosphère neutre.
Dans le cas d'une atmosphère stable, où l'on s'attend à des mouvements
anisotropes plutôt horizontaux,
dans le cas d'une turbulence isotrope en atmosphère neutre.
Dans le cas d'une atmosphère stable, où l'on s'attend à des mouvements
anisotropes plutôt horizontaux, ![]() fournira plutôt
une surestimation de
fournira plutôt
une surestimation de
![]() (respectivement une sous-estimation
pour une atmosphère instable).
(respectivement une sous-estimation
pour une atmosphère instable).
Sous les hypothèses de couche limite mentionnées plus haut,
on peut montrer (voir e. g. Stull, 1988) que l'évolution de
l'énergie cinétique turbulente s'écrit sous la forme
| (3.12) |
| (3.13) |
| (3.14) |
Mellor et Yamada, à partir d'une paramétrisation des termes du troisième
ordre (à la base il s'agit donc d'une fermeture à l'ordre 2) proposent
une série de simplifications, avec une hiérarchie de schémas.
Nous présentons ici le schéma de niveau 2.5 (qui malgré cette nomenclature
originale n'est qu'une approximation relativement grossière d'un schéma
d'ordre 2), le plus largement testé dans des
applications météorologiques, et dont certains résultats sont présentés
plus loin.
Dans le modèle 2.5, les termes croisés s'écrivent formellement, comme pour la
diffusion turbulente,
| (3.15) |
Un des tours de force de ce travail est de faire sortir directement
de simplifications successives d'une fermeture du second ordre
une formulation analytique pour les fonctions ![]() et
et ![]() .
Ces grandeurs sont fonctions du seul nombre de Richardson de flux,
.
Ces grandeurs sont fonctions du seul nombre de Richardson de flux,
![]() , mesure de l'importance relative du forçage
mécanique de la turbulence et de l'inhibition par stratification.
On retient ici
les valeurs numériques données par
Yamada (1983). Cette version a été utilisée dans une étude d'intercomparaison
de fermetures turbulentes par Ayotte et al. (1996). Elle est également utilisée
plus loin dans des tests numériques. Pour la quantité de
mouvement, on obtient :
, mesure de l'importance relative du forçage
mécanique de la turbulence et de l'inhibition par stratification.
On retient ici
les valeurs numériques données par
Yamada (1983). Cette version a été utilisée dans une étude d'intercomparaison
de fermetures turbulentes par Ayotte et al. (1996). Elle est également utilisée
plus loin dans des tests numériques. Pour la quantité de
mouvement, on obtient :
| (3.16) |
| (3.17) |
| (3.18) |
| (3.19) |
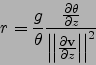 |
(3.20) |
| (3.21) |
| (3.22) |
Dans le modèle 2.5, le terme de pression est négligé et le transport
vertical est traité comme une diffusion turbulente
de sorte que l'évolution de l'énergie
cinétique turbulente ou de ![]() s'écrit finalement
s'écrit finalement
La paramétrisation de Mellor et Yamada, même dans ses versions plus
sophistiquées, laisse en fait une grosse zone d'ombre sur la spécification de la
longueur de mélange ![]() . Dans certains articles, les auteurs ont
suggéré une équation pour
. Dans certains articles, les auteurs ont
suggéré une équation pour ![]() analogue à l'équation pour
analogue à l'équation pour ![]() mais
cette équation est beaucoup moins fondée que sa grande s
mais
cette équation est beaucoup moins fondée que sa grande s![]() ur (selon
les auteurs eux-mêmes).
Le plus souvent, la longueur de mélange est spécifiée, par exemple
en utilisant la formule de Blackadar (1962)
ur (selon
les auteurs eux-mêmes).
Le plus souvent, la longueur de mélange est spécifiée, par exemple
en utilisant la formule de Blackadar (1962)
| (3.24) |
| (3.25) |
|
Avant de la tester couplée au modèle du thermique dans la version
terrestre de LMDZ (comme on l'explique plus loin), nous avons avec Richard
Fournier introduit la fermeture 2.5 de
de Mellor et Yamada dans la version martienne du modèle
(Forget et al., 1999).
Avec sa fine atmosphère de CO![]() , l'immense désert martien connaît
des cycles diurnes très marqués.
Dans les tropiques, ou l'été dans les moyennes latitudes, la température
de surface peut varier de plusieurs dizaines de degrés entre la nuit
et le jour.
On montre sur la Fig. 3.1 un exemple de comparaison de résultats
de simulations numériques avec des observations par les sondes Viking.
On voit sur cette figure
un cas typique de jet nocturne comme il en existe dans les déserts
terrestres. Le mélange vertical intense pendant
la journée s'éteint subitement en fin d'après-midi (voir la brusque chute
de
, l'immense désert martien connaît
des cycles diurnes très marqués.
Dans les tropiques, ou l'été dans les moyennes latitudes, la température
de surface peut varier de plusieurs dizaines de degrés entre la nuit
et le jour.
On montre sur la Fig. 3.1 un exemple de comparaison de résultats
de simulations numériques avec des observations par les sondes Viking.
On voit sur cette figure
un cas typique de jet nocturne comme il en existe dans les déserts
terrestres. Le mélange vertical intense pendant
la journée s'éteint subitement en fin d'après-midi (voir la brusque chute
de ![]() sur les figures c). Le vent qui était dans l'après-midi
en équilibre entre un gradient de pression et ce terme de mélange
se trouve subitement en déséquilibre et entre en oscillation inertielle.
Dans les premières couches du modèle,
le vent diminue rapidement sous l'effet du frottement
turbulent sur la surface tandis que les couches supérieures, découplées
de la surface, accélèrent.
On obtient alors en sommet de couche limite une couche fortement cisaillée
qui génère à nouveau de la turbulence.
Les comparaisons aux données sont bonnes en générale pour les quantités
moyennes ainsi que pour l'énergie cinétique turbulente la nuit.
On note cependant une très forte sous-estimation
des fluctuations turbulentes du vent le jour, dues sans
doute à la non prise en compte des mouvement convectifs (comme on
l'explique plus loin).
sur les figures c). Le vent qui était dans l'après-midi
en équilibre entre un gradient de pression et ce terme de mélange
se trouve subitement en déséquilibre et entre en oscillation inertielle.
Dans les premières couches du modèle,
le vent diminue rapidement sous l'effet du frottement
turbulent sur la surface tandis que les couches supérieures, découplées
de la surface, accélèrent.
On obtient alors en sommet de couche limite une couche fortement cisaillée
qui génère à nouveau de la turbulence.
Les comparaisons aux données sont bonnes en générale pour les quantités
moyennes ainsi que pour l'énergie cinétique turbulente la nuit.
On note cependant une très forte sous-estimation
des fluctuations turbulentes du vent le jour, dues sans
doute à la non prise en compte des mouvement convectifs (comme on
l'explique plus loin).
On peut aller un cran plus loin dans les simplifications en supposant
que les termes de production ou destruction d'énergie turbulente et la
dissipation sont constamment à l'équilibre ![]() ,
d'où l'on tire
,
d'où l'on tire
| (3.31) |
| (3.32) |
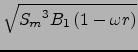 ) rendant compte des
effets de la stratification.
) rendant compte des
effets de la stratification.
La formulation utilisée dans le modèle original du LMD (Laval et al., 1981)
est également basée sur un modèle stationnaire de l'énergie cinétique
turbulente. Seuls les coefficients diffèrent.
Le coefficient de mélange s'écrit simplement sous la forme
| (3.33) |
Dans le monde des sciences de l'ingénieur, les fermetures dites
![]() sont davantage utilisées que le modèle de Mellor et Yamada.
Ces fermetures font intervenir
deux équations pronostiques, l'une pour l'énergie
turbulente
sont davantage utilisées que le modèle de Mellor et Yamada.
Ces fermetures font intervenir
deux équations pronostiques, l'une pour l'énergie
turbulente ![]() et l'autre pour la dissipation
et l'autre pour la dissipation ![]() .
.
Les méthodes de similitude ont remporté un grand succès
dans l'explication des observations des grandeurs turbulentes dans
la couche limite de surface.
Dans cette approche, on s'intéresse à une couche limite en régime stationnaire,
on adimensionalise les équations et on dérive des relations ou modèles
à partir des seuls paramètres dont dépendent les équations.
La couche logarithmique, présentée plus haut à partir de la longueur
de mélange, peut déjà être présentée à partir des relations
de similitude si on remarque que le gradient vertical du vent
près de la surface dans une atmosphère neutre ne peut dépendre que
de ![]() et
et ![]() .
.
Monin et Obukov ont introduit les effets de la stratification dans
cette description de la turbulence mécanique.
L'hypothèse de base de leur théorie est de supposer que le cisaillement
adimensionnel,
![]() , égal à 1 pour une atmosphère
neutre, ne dépend que d'une mesure de l'importance relative des flux de moment
et de chaleur, le nombre de Richardson de flux
, égal à 1 pour une atmosphère
neutre, ne dépend que d'une mesure de l'importance relative des flux de moment
et de chaleur, le nombre de Richardson de flux ![]() introduit plus haut.
Dans la couche de surface, ce nombre s'écrit
introduit plus haut.
Dans la couche de surface, ce nombre s'écrit
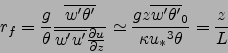 |
(3.34) |
| (3.35) |
On suppose donc, dans la couche de surface, que le gradient de vent peut
s'écrire sous la forme
| (3.36) |
| (3.37) |
![\begin{displaymath}
\psi_m\left(\xi\right)=\int_{z_0/L}^{\xi}\left[1-\phi_m\left...
...0 }^{\xi}\left[1-\phi_m\left(\xi\right)\right]\frac{d\xi}{\xi}
\end{displaymath}](img518.png) |
(3.38) |
Comme pour la quantité de mouvement, on suppose que le gradient de température
adimensionnel est relié au gradient neutre par une fonction de ![]()
| (3.39) |
| (3.40) |
Des campagnes de mesures ont été dédiées à la mesure de ces fonctions. Les formules proposées par Businger et al. (1971) et ajustées sur les résultats d'une campagne dans le Kansas sont encore largement utilisées. Ces formules sont données dans la Table 3.1. De nombreuses versions modifiées ont été proposées depuis, utilisant parfois des données plus récentes (cf. par exemple Högström, 1988).
|
Notons que Mellor (1973) a appliqué son modèle de fermeture à la couche limite de surface, en supposant des flux constants, et réussi à interpréter les mesures de Businger et al. (1971) avec des jeux de coefficients compatibles avec des mesures de souffleries en conditions neutres.
Certains auteurs ont essayé d'extrapoler les approches en similitude
à la couche mélangée. Il faut alors introduire au moins
un paramètre supplémentaire : la hauteur de la couche limite ![]() .
Nous testons par exemple plus loin
une formulation analytique du coefficient de diffusion turbulente
en fonction de l'altitude proposée à l'origine par Brost et Wyngaard (1978)
.
Nous testons par exemple plus loin
une formulation analytique du coefficient de diffusion turbulente
en fonction de l'altitude proposée à l'origine par Brost et Wyngaard (1978)
| (3.41) |
Pour appliquer cette formule, il faut commencer par estimer
la hauteur de la couche limite ![]() .
Une approche maintenant classique et relativement robuste
consiste à utiliser un nombre de Richardson non local :
.
Une approche maintenant classique et relativement robuste
consiste à utiliser un nombre de Richardson non local :
A la base, les formulations - plus ou moins sophistiquées - en diffusion turbulente font l'hypothèse que la longueur caractéristique des mouvements turbulents est petite devant les échelles spatiales typiques, et notamment devant la hauteur de la couche limite.
Les limites de cette approche sont reconnues depuis longtemps, en particulier dans le cas des couches limites convectives, où les ascendances thermiques, résultant de l'accumulation de chaleur près de la surface, s'organisent sous forme de panaches ou de rouleaux à des échelles comparables aux échelles de la couche limite. Dans la suite, on appellera meso-échelle cette échelle des structures convectives de couche limite. Dans la couche limite convective, le flux de chaleur, dirigé vers le haut pour évacuer l'énergie accumulée à la surface, est souvent associé à un profil neutre ou même marginalement stable de température potentielle, c'est à dire que le flux d'énergie remonte le gradient, du froid vers le chaud, ce qui est incompatible avec une approche en diffusion.
Les couches limites convectives se caractérisent plus précisément en trois régions :
- une couche de surface instable chauffée directement par le sol,
- une couche mélangée épaisse typiquement de 1 à 2 km dans les régions
tempérées
mais qui peut atteindre 3 km aux jours les plus chauds de l'été même en
région parisienne et plus de
5 km sur les déserts ou sur la planète Mars.
- une couche d'inversion très stable, épaisse de quelques dizaines à
quelques centaines de mètres.
La hauteur de cette inversion ![]() est souvent utilisée comme hauteur de couche limite.
3.2
est souvent utilisée comme hauteur de couche limite.
3.2
Ce sont
les particules d'air de la couche de surface,
particules plus chaudes donc plus légères que celles de la
couche mélangée,
qui s'élèvent dans la couche mélangée pour s'organiser en
ascendances thermiques sous forme de rouleaux, de cellules ou de
panaches isolés.
L'accélération d'une particule ![]() de la couche de surface
dans l'environnement
de la couche de surface
dans l'environnement ![]() est donnée par
est donnée par
| (3.43) |
| (3.44) |
Avant de présenter quelques approches pour paramétriser la couche limite dans ces conditions particulières, et de décrire en détail le ``modèle du thermique", on présente dans cette section une analyse d'échelle de la couche limite convective ainsi que les grandes lignes des connaissances sur le sujet, que ce soit au travers d'observations ou de simulations dites des grands tourbillons (ou Large Eddy Simulation en anglais).
Parce que les développements proposés ici concernent essentiellement la couche limite convective en ciel clair, on ne parlera pratiquement pas de nuages, même s'il est clair que la capacité de la nouvelle paramétrisation à prédire les caractéristiques statistiques des nuages (couverture nuageuse, contenu en eau des nuages) sera un élément essentiel de sa possible adoption comme paramétrisation de base d'un modèle de climat.
L'existence de structures organisées dans la couche limite convective
est bien connue des amateurs de vol libre
qui utilisent les ``pompes" thermiques pour gagner de l'altitude.
Les vitesses verticales rapportées par ces amateurs sont typiquement
de 1 à 4 m s![]() en plaine et plutôt de 5 à 10 m s
en plaine et plutôt de 5 à 10 m s![]() en montagne.
en montagne.
Ces structures peuvent prendre la forme de panaches isolés ou s'organiser en forme de cellules ou de rouleaux. Un travail d'investigation systématique de ces structures, notamment à partir de vols avions, a été entrepris depuis une trentaine d'années, à partir des travaux pionniers de LeMone (1973). Les mesures in-situ à bord d'avions, les photos satellites à haute résolution, les instruments de détections active (radar et lidar) ainsi que les simulations numériques dites ``des grands tourbillons" (Large Eddy Simulations en anglais) ont permis de mieux comprendre et caractériser les structures organisées de la couche limite. On se contente ici de montrer quelques illustrations issues de ces études.
Les rues de nuages constituent une des réalisations les plus spectaculaire de l'organisation de la convection de couche limite. Les structures de rues s'observent à toutes les latitudes et en toutes saisons, mais les arrivées sur la mer d'air très froid ayant séjourné un moment sur des glaciers ou des banquises offrent souvent des photos spectaculaires comme celle montrée sur la Fig. 3.2. L'air froid et sec, en arrivant sur la mer plus chaude (ici le vent souffle du nord au milieu de la mer de Bering) donne naissance à une couche limite convective. Au début, l'air est encore clair. Il se charge petit à petit en humidité et des cumulus se mettent à bourgeonner en sommet de la partie ascendante de grands rouleaux convectifs, créant ces grandes rues de nuages alignées le long du vent dominant. L'image faisant un millier de kilomètres de large environ, on voit que les rues de nuages sont typiquement espacées de 5 km dans la partie nord et jusqu'à une vingtaine dans le sud.
Au sud de la zone, la structure en rouleaux disparaît au profit d'une organisation en cellules. Mais, dans un cas comme dans l'autre, on distingue nettement une organisation à une échelle de quelques kilomètres à quelques dizaines de kilomètres.
A noter également, dans le sud-ouest de la photo, au sud (en aval) des Aléoutiennes, des structures transversales associées très vraisemblablement à des ondes de gravité piégées dans le sillage des reliefs que constituent les îles.
B : domaine de 3 SB1 : domaine de 5 |
De nombreux travaux théoriques et numériques ont été consacrés à l'étude de ces structures convectives de la couche limite.
Une étude théorique des instabilité de la couche d'Eckman a permis
de prédire l'orientation des rouleaux par rapport aux vents dominants
(Brown, 1972). Les rouleaux sont alignés à 30![]() à gauche
du vent pour des couches stables, 18
à gauche
du vent pour des couches stables, 18![]() pour des couches limites
neutres et essentiellement alignées avec le vent pour des couches instables.
Le modèle de la couche d'Eckman n'est pas vraiment applicable à la couche
limite instable mais la prédiction est cependant relativement
proche de l'observation (LeMone, 1973) même si les rouleaux sont plutôt
orientés également à 10-20
pour des couches limites
neutres et essentiellement alignées avec le vent pour des couches instables.
Le modèle de la couche d'Eckman n'est pas vraiment applicable à la couche
limite instable mais la prédiction est cependant relativement
proche de l'observation (LeMone, 1973) même si les rouleaux sont plutôt
orientés également à 10-20![]() du vent dans la couche convective.
On montre sur la Fig. 3.3 une vision schématique de cette organisation
en rouleaux.
du vent dans la couche convective.
On montre sur la Fig. 3.3 une vision schématique de cette organisation
en rouleaux.
Après le travail pionnier de Sommeria et LeMone (1978),
de nombreuses simulations des grands tourbillons ont été consacrées
à l'organisation de la couche limite convective.
Dans les simulations des grands tourbillons,
on résout explicitement des équations
dynamiques non-hydrostatiques (différentes approximations sont cependant
utilisées pour filtrer les modes acoustiques les plus rapides)
jusqu'à une échelle typique de 20 à 100 m suivant les cas.
On suppose à cette échelle que la turbulence est bien représentée par
des idées de cascades vers les petites échelles et par des fermetures
locales de type ![]() ou Mellor et Yamada.
A partir de telles simulations,
Moeng et Sullivan (1994) et d'autres ont par exemple
montré que la sélection entre les différents
modes d'organisation était en grande partie contrôlée par l'importance
relative des forçages thermiques (par le chauffage en surface)
et mécanique (par le cisaillement de vent) de la turbulence.
ou Mellor et Yamada.
A partir de telles simulations,
Moeng et Sullivan (1994) et d'autres ont par exemple
montré que la sélection entre les différents
modes d'organisation était en grande partie contrôlée par l'importance
relative des forçages thermiques (par le chauffage en surface)
et mécanique (par le cisaillement de vent) de la turbulence.
Les simulations de Moeng et Sullivan (1994) sont relativement académiques, avec
une turbulence de couche limite
forcée par un flux de chaleur imposé
en surface et un forçage géostrophique engendrant des cisaillements de
vent et donc de la turbulence mécanique près de la surface.
Il s'agit de couches limites non nuageuses.
Le calcul est effectué sur un domaine carré de 3 ou 5 km avec une maille
d'une cinquantaine de mètres dans les trois directions d'espace et
des conditions aux limites périodiques horizontalement.
En faisant varier indépendamment l'intensité du forçage thermique
![]() en surface et l'intensité du vent géostrophique
en surface et l'intensité du vent géostrophique ![]() ,
on trouve dans les simulations
deux modes d'organisation : une organisation en rouleaux quand le
cisaillement est important et des panaches isolés sans organisation apparente
quand le flux de chaleur domine.
Sur la Fig. 3.4, on montre des coupes instantanées à l'altitude
,
on trouve dans les simulations
deux modes d'organisation : une organisation en rouleaux quand le
cisaillement est important et des panaches isolés sans organisation apparente
quand le flux de chaleur domine.
Sur la Fig. 3.4, on montre des coupes instantanées à l'altitude
![]() , où
, où ![]() est la hauteur de l'inversion,
des perturbations de la vitesse
verticale (en haut) et de la température potentielle virtuelle
(en bas) pour deux simulations.
Dans la première - appelée B pour ``buoyant" par les auteurs -
le flux en surface vaut
est la hauteur de l'inversion,
des perturbations de la vitesse
verticale (en haut) et de la température potentielle virtuelle
(en bas) pour deux simulations.
Dans la première - appelée B pour ``buoyant" par les auteurs -
le flux en surface vaut
![]() m K s
m K s![]() avec un vent géostrophique
avec un vent géostrophique ![]() de 10 m s
de 10 m s![]() .
Dans la seconde simulation, le forçage mécanique est plus important avec
.
Dans la seconde simulation, le forçage mécanique est plus important avec
![]() m K s
m K s![]() et
et ![]() =15 m s
=15 m s![]() .
Cette simulation avec cisaillement et flottabilité (shear and buoyancy)
est appelée SB1 par les auteurs.
.
Cette simulation avec cisaillement et flottabilité (shear and buoyancy)
est appelée SB1 par les auteurs.
Pour les deux simulations, on voit clairement les structures thermiques, avec de l'air chaud associé à des vitesses ascendantes. Ces structures thermiques couvrent dans les deux cas une fraction relativement faible de la surface. La simulation B ne présente pas de structure bien marquée et on a plutôt l'impression de voir des panaches isolés. La simulation SB1, avec un forçage mécanique important, présente une organisation en rouleaux. La relative faible étendue du domaine fait qu'on ne simule que deux rouleaux. Des simulations plus récentes, utilisant des domaines plus grands par rapport aux structures représentées, confirment ces résultats (cf. par exemple Weckwerth et al., 1997).
Les subsidences amènent vers la surface de l'air provenant du haut
du domaine et associé de ce fait à un excès de quantité de mouvement
(le vent géostrophique ![]() est positif dans la direction
est positif dans la direction ![]() )
comme on le voit sur la Fig. 3.5 pour la simulation SB1.
En
)
comme on le voit sur la Fig. 3.5 pour la simulation SB1.
En ![]() , sur la gauche de la figure,
les structures organisées sont encore perturbées par les
organisations à plus petite échelle dans la couche limite de surface.
Un peu plus haut dans l'atmosphère et à droite sur la même
figure, en
, sur la gauche de la figure,
les structures organisées sont encore perturbées par les
organisations à plus petite échelle dans la couche limite de surface.
Un peu plus haut dans l'atmosphère et à droite sur la même
figure, en ![]() , la structure
en rouleaux domine encore davantage l'écoulement.
, la structure
en rouleaux domine encore davantage l'écoulement.
Dans ces simulations, le rapport d'aspect - rapport entre la séparation des rouleaux et la hauteur de la couche limite - est compris entre 2 et 3.
L'importance de l'organisation en cellules ou en rouleaux de la couche limite convective, même en l'absence de nuages, a été confirmée avec l'utilisation de plus en plus systématique de la télédétection active, lidar ou radar, pour observer l'atmosphère. Les échos lidar ou radar sont en effet souvent capables de distinguer, dans la couche limite, l'air montant depuis la couche de surface de son environnement. Pour les lidars, c'est la présence d'aérosols dans les panaches qui permet en général de les visualiser alors que, pour les radars, on pense qu'on voit souvent des insectes.
On montre sur la Fig. 3.6 deux exemples d'observations radar issus d'une étude de Weckwerth et al. (1997) montrant à gauche une organisation en rouleaux et, à droite, une organisation en cellules. Cette étude assez systématique d'observation de la couche limite convective en Floride a permis de confirmer certains résultats obtenus avec les simulations des grands tourbillons, comme l'apparition systématique de rouleaux dans certaines gammes de cisaillement et de flux de chaleur ou l'estimation du rapport d'aspect des rouleaux.
Des couches limites convectives particulièrement développées sont observées l'après-midi sur les continents, notamment par beau temps. Sur les déserts, elles peuvent atteindre plus de 5 km d'altitude. On montre sur la Fig. 3.7 un exemple d'observations de couches limites convectives sur trois jours consécutifs au SIRTA, le site instrumenté atmosphérique de l'IPSL. Les figures de droite montrent l'écho lidar (le lidar LNA3.3) observé au cours du temps à la verticale de l'école Polytechnique, à Palaiseau. Sur ces figures, la couche limite est matérialisée grossièrement comme la zone gris clair, correspondant à une réflexion sur des aérosols. La couche limite nocturne très fine (quelques centaines de mètres) se développe dans la matinée, entre 9 heures et midi. Dans cette phase de croissance, on voit très clairement des panaches ascendants, plus clairs que l'air environnant. En début d'après-midi, la couche limite convective est bien développée et on voit se former, au sommet des thermiques, des cumulus qui réfléchissent totalement le signal.
Les profils de température potentielle associés,
observés à Trappes par radiosondage à
midi, montrent tous les trois une légère instabilité dans la couche de surface
et un profil très bien mélangé sur 1 à 1,5 km suivant les jours.
Dans cette région, l'humidité spécifique est relativement bien mélangée
également. Ceci correspond à une humidité relative qui croît avec l'altitude,
pour approcher les 100![]() en sommet de couche limite, là où les
nuages sont observés.
en sommet de couche limite, là où les
nuages sont observés.
Cette pulsation de la couche limite entre couche limite nocturne stable et couche limite convective développée dans l'après-midi conditionne au premier chef les concentrations observées pour les espèces émises en surface.
On montre également sur la Fig. 3.8 des mesures radar aéroportées obtenues pendant la campagne IHOP qui s'est déroulée pendant l'été 2002 dans l'Oklaoma. Là encore, on voit se développer les thermiques en cours de matinée. On voit également que les petits thermiques du matin s'organisent peu à peu en ascendances plus importantes et plus espacées.
Depuis les travaux de LeMone (1973), de nombreux travaux ont porté sur la caractérisation des ascendances thermiques à partir des mesures avions.
Pour quantifier les fluctuations turbulentes, on effectue
des vols en avion aussi stables que possible en altitude avec
un échantillonnage rapide, et on analyse les
fluctuations de vent, température et humidité.
Un exemple de séquence de mesure de la température potentielle et de
la vitesse verticale est donné en haut de la Fig. 3.9.
Pour cet exemple, issu du travail de Williams et Hacker (1992),
la fréquence d'acquisition
était de 13 Hz ce qui correspond, pour un avion qui volait en moyenne
à 40 m s![]() , à un pas d'échantillonnage d'environ 3 m.
, à un pas d'échantillonnage d'environ 3 m.
On voit clairement apparaître sur ce cas particulier des évènements chauds, d'une longueur d'une centaine de mètres, associés à une vitesse verticale plutôt positive mais très bruitée.
La façon la plus classique d'analyser de telles observations consiste à
calculer les flux par corrélation entre fluctuations de vent et
de température (
![]() ).
Cette approche permet effectivement d'estimer les flux mais en perdant
toute l'information sur les structures organisées.
Il est en plus délicat de restituer la géométrie des
structures méso-échelles traversées à partir des vols avions.
En effet, les variations verticales ne peuvent être reconstituées qu'au
travers de vols horizontaux successifs et qui n'explorent donc pas
les mêmes panaches thermiques.
).
Cette approche permet effectivement d'estimer les flux mais en perdant
toute l'information sur les structures organisées.
Il est en plus délicat de restituer la géométrie des
structures méso-échelles traversées à partir des vols avions.
En effet, les variations verticales ne peuvent être reconstituées qu'au
travers de vols horizontaux successifs et qui n'explorent donc pas
les mêmes panaches thermiques.
Williams et Hacker (1992) ont proposé une approche très éclairante sur la nature
du transport dans la couche limite convective à partir de la construction
d'un thermique moyen, défini comme un composite des évènements
chauds. Les thermiques sont en général beaucoup plus facilement
identifiables sur les mesures de ![]() , qui montrent une grande
asymétrie entre un fond un peu froid et des évènements chauds intenses
et relativement bien isolés, que sur celles du vent.
Pour caractériser ces thermiques, Williams et Hacker (1992) commencent donc
par identifier les segments chauds sur les mesures de
, qui montrent une grande
asymétrie entre un fond un peu froid et des évènements chauds intenses
et relativement bien isolés, que sur celles du vent.
Pour caractériser ces thermiques, Williams et Hacker (1992) commencent donc
par identifier les segments chauds sur les mesures de ![]() -
après un lissage - comme les portions où
-
après un lissage - comme les portions où ![]() dépasse
1
dépasse
1![]() où
où ![]() est l'écart-type
des fluctuations.
Tous les segments sont ensuite ramenés par homothétie sur un segment
de longueur unité.
On peut alors, à partir de tout ces segments, calculer des moyennes ou
écart-types de toutes les grandeurs mesurées pour construire une
image d'un thermique moyen.
Cette méthode est illustrée sur la Fig. 3.9.
est l'écart-type
des fluctuations.
Tous les segments sont ensuite ramenés par homothétie sur un segment
de longueur unité.
On peut alors, à partir de tout ces segments, calculer des moyennes ou
écart-types de toutes les grandeurs mesurées pour construire une
image d'un thermique moyen.
Cette méthode est illustrée sur la Fig. 3.9.
Sur la Fig. 3.10, on montre les résultats obtenus par Williams et Hacker (1992)
à différents niveaux dans la couche limite convective.
Les différentes variables sont normalisées par des échelles caractéristiques.
Pour le vent vertical, l'échelle utilisée est l'échelle convective
(proposée à l'origine par Deardorff, 1970)
construite à partir du flux de chaleur au sol et de la
hauteur de la couche limite ![]() :
:
![\begin{displaymath}
\theta_*=\frac{\overline{w'\theta'}_0}{w_*}=
\left[\frac{g}{...
...\right]^{-\frac{1}{3}}
{\overline{w'\theta'}_0 }^{\frac{2}{3}}
\end{displaymath}](img581.png) |
(3.46) |
On retrouve sur ces composites des caractéristiques déjà suggérées par
l'observation directe des séquences avions.
Les thermiques, sélectionnés à partir d'un excès
de température, sont aussi associés à un vent vertical positif en moyenne.
La valeur du vent ascendant au milieu du thermique est
très proche de l'échelle de vitesse ![]() alors que
l'écart type (en pointillé) est de l'ordre de grandeur du vent moyen dans
et à proximité du thermique pour la vitesse ascendante.
Ceci suggère que le thermique et ses abords immédiats sont le
siège d'une turbulence de petite échelle importante, le thermique
n'expliquant à lui seul que la moitié environ de
alors que
l'écart type (en pointillé) est de l'ordre de grandeur du vent moyen dans
et à proximité du thermique pour la vitesse ascendante.
Ceci suggère que le thermique et ses abords immédiats sont le
siège d'une turbulence de petite échelle importante, le thermique
n'expliquant à lui seul que la moitié environ de
![]() .
En regard,
l'écart-type est deux à trois fois plus faible que la moyenne pour la
température.
.
En regard,
l'écart-type est deux à trois fois plus faible que la moyenne pour la
température.
Le flux de chaleur dans l'ascendance est 4 fois supérieur au chauffage par
la surface en bas et encore 2 à 3 fois supérieur au milieu de la couche
mélangée alors qu'il est beaucoup plus faible autour.
Les thermiques qui occupent typiquement 20![]() de la surface dans
les observations, semblent donc, à eux seuls, capables d'expliquer
l'essentiel du transport de chaleur.
de la surface dans
les observations, semblent donc, à eux seuls, capables d'expliquer
l'essentiel du transport de chaleur.
Dans le cas considéré, la vapeur d'eau est légèrement plus abondante dans le panache, mais avec une grande dispersion.
A noter qu'en regard de cette analyse en composites particulièrement éclairante, il existe une littérature relativement abondante dans laquelle les thermiques sont caractérisés sur la base de seuils sur les vitesses verticales. Ces études suggèrent qu'une fraction seulement (typiquement une bonne moitié) du flux de chaleur est contenu dans les plus grandes structures. On citera en particulier pour ces questions le travail de Schumann et Moeng (1991) qui compare des tris en vitesse verticale à la fois dans des simulations des grands tourbillons et dans des observations et le travail de Wang (1996) qui étudient l'influence du choix du seuil sur la caractérisation des structures organisées. Le tri sur les vitesses verticales est en fait particulièrement peu sélectif des thermiques car les variations turbulentes du vent sont dues aussi bien aux structures méso-échelles qu'à la turbulence de petite échelle, active dans toute la couche limite. Les fluctuations de petite échelle, en mélangeant un air déjà bien mélangé, n'affectent que peu les fluctuations turbulentes de la température. Les excès de température sont donc davantage caractéristiques de l'origine de l'air.
On voit donc que les structures thermiques sont associées à des distributions
de fluctuations turbulentes de ![]() ou
ou ![]() fortement asymétrique.
Ces distributions peuvent être calculées dans les simulations des grands
tourbillons.
On montre pour illustration sur la Fig. 3.11, les distributions
de
fortement asymétrique.
Ces distributions peuvent être calculées dans les simulations des grands
tourbillons.
On montre pour illustration sur la Fig. 3.11, les distributions
de ![]() et
et ![]() obtenues avec le modèle Meso-NH pour une
simulation d'un jour particulier de la campagne IHOP (Couvreux, 2005),
correspondant aux mesures radar aéroportées de la Fig. 3.8.
La distribution croisée de
obtenues avec le modèle Meso-NH pour une
simulation d'un jour particulier de la campagne IHOP (Couvreux, 2005),
correspondant aux mesures radar aéroportées de la Fig. 3.8.
La distribution croisée de ![]() et
et ![]() montre un maximum important
pour des températures basses et des vitesses verticales légèrement
négatives et des températures plus chaudes associées à des vitesses
verticales positives et plus importantes, les thermiques.
Les distributions individuelles des deux variables montrent une forte
asymétrie avec une queue de distribution du côté des vitesses positives et
des températures chaudes.
Pour
montre un maximum important
pour des températures basses et des vitesses verticales légèrement
négatives et des températures plus chaudes associées à des vitesses
verticales positives et plus importantes, les thermiques.
Les distributions individuelles des deux variables montrent une forte
asymétrie avec une queue de distribution du côté des vitesses positives et
des températures chaudes.
Pour ![]() , la forme de la distribution est en très bon accord avec
celle déduite de vols avions (non montrées).
, la forme de la distribution est en très bon accord avec
celle déduite de vols avions (non montrées).
Dans la couche mélangée, le transport de chaleur est donc
effectué principalement
par les structures de grande échelle avec des ascendances, associées
à de l'air plus chaud provenant de la couche limite de surface, compensées
par des subsidences plus froides.
Si on idéalise l'ascendance thermique en supposant
qu'elle est associée à un excès constant, ![]() ,
de température potentielle virtuelle3.4et une vitesse verticale
,
de température potentielle virtuelle3.4et une vitesse verticale ![]() (=
(=![]() ) et
si on suppose que les particules d'air dans le thermique
montent sous l'effet de leur flottabilité, on a, avec l'approximation
classique
) et
si on suppose que les particules d'air dans le thermique
montent sous l'effet de leur flottabilité, on a, avec l'approximation
classique
![]() ,
,
| (3.47) |
| (3.48) |
Si on suppose que les
ascendances couvrent une fraction ![]() de la surface
et qu'elles sont compensées par une subsidence de
vitesse moyenne
de la surface
et qu'elles sont compensées par une subsidence de
vitesse moyenne ![]() , associée à un déficit moyen de température
potentielle
, associée à un déficit moyen de température
potentielle ![]() avec :
avec :
| (3.50) |
| (3.51) |
| (3.52) |
On obtient donc (en utilisant l'Eq. 3.49)
une relation entre le flux de chaleur et la vitesse
dans les ascendances
La couche limite convective est par nature très brassée et elle se caractérise donc par un profil de température potentielle très homogène. De ce fait un excès de température en surface se répartit très rapidement dans l'ensemble de la couche mélangée. Le flux de chaleur fourni par la surface produit donc un réchauffement quasi uniforme de la couche limite, jusqu'à la couche d'inversion. En conséquence aussi, la divergence du flux de chaleur doit être nulle dans la couche mélangée, c'est à dire que le flux doit décroître linéairement depuis la surface.
Cette idée est illustrée sur la Fig. 3.12. La courbe noire à gauche montre un profil typique de température potentielle dans la couche limite convective, avec une couche de surface instable, une couche mélangée neutre et une inversion en sommet de couche limite. Le flux de chaleur en surface brasse la couche mélangée provoquant un chauffage homogène de la couche mélangée et un léger refroidissement au niveau de l'inversion. Le schéma du milieu montre le flux moyen de chaleur associé à cette évolution de la température potentielle. La dérivée du flux de chaleur s'annule à l'altitude où la température n'évolue pas.
Pour l'analyse d'échelle, on voit donc que le flux de chaleur décroît
linéairement pour s'annuler à une altitude légèrement inférieure à ![]() .
Si on se place au milieu de la couche limite en
.
Si on se place au milieu de la couche limite en ![]() , le flux
calculé par l'Eq. 3.53 doit être proche de
, le flux
calculé par l'Eq. 3.53 doit être proche de
![]() d'où
d'où
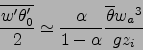 |
(3.54) |
![\begin{displaymath}
w_a\simeq w_*{\left[\frac{1-\alpha}{2\alpha}\right]}^{\frac{1}{3}}
\end{displaymath}](img604.png) |
(3.55) |
Avant de présenter le modèle du thermique, on donne ci-dessous un aperçu des différentes approches qui ont été proposées ou utilisées pour pallier les déficiences de la diffusion turbulente dans les cas de couches limites convectives.
Une première approche simple pour pallier le problème du transport de chaleur en remontant le gradient dans la couche limite, consiste à calculer la diffusion, non pas par rapport à un profil neutre de température potentielle mais par rapport à un profil légèrement stable.
Cette approche a été proposée par Deardorff (1966) et consiste
à prescrire le flux de chaleur sous la forme
| (3.56) |
Plusieurs études (notamment par Deardorff lui-même) ont tenté de donner une expression physique de ce contre-gradient mais les modèles de circulation utilisent souvent une valeur constante de l'ordre de 0,5 K/km. La prescription d'un tel contre-gradient est encore de mise dans le modèle du LMD.
Plus récemment, Holtslag et Boville (1993) ont introduit, dans le modèle du NCAR,
un schéma de couche limite non local qui inclut un terme de contre-gradient
relié directement aux caractéristiques de la couche limite, en suivant
une approche développée à l'origine par Troen et Mahrt (1986).
Dans cette approche, le coefficient de mélange est prescrit en suivant un profil
à la Brost et Wyngaard (1978)
| (3.57) |
| (3.58) |
| (3.59) |
| (3.60) |
La paramétrisation de Holtslag et Boville (1993) permet d'étendre le transport non local aux traceurs.
Bougeault et Lacarrere (1989) ont également développé une paramétrisation en partie non locale en utilisant une longueur de mélange reliée à la distance qu'une particule d'air, issue du niveau considéré, peut parcourir après qu'on lui a donné au départ une impulsion correspondant à l'énergie cinétique turbulente moyenne dans la couche en question. Notons que cette approche est non locale mais qu'elle ne permet pas le transport en remontant le gradient.
Abdella et McFarlane (1997) ont pour leur part proposé de modifier la fermeture du second ordre de Mellor et Yamada (1974) en paramétrisant les moments du second ordre en utilisant des images en flux de masses comme celles qui sont développées plus loin dans le modèle du thermique. Comme dans le travail de Troen et Mahrt (1986), on aboutit alors à une expression physique d'un terme de contre-gradient.
Toutes ces approches ont en commun qu'elles essaient d'introduire des aspects non locaux dans un formalisme hérité des formulations locales en diffusion turbulente ou dans des développements à des ordre successifs d'équations locales de la turbulence.
Depuis les années 1980, Stull insiste, parfois lourdement, sur
la nécessité de rompre radicalement avec la diffusion turbulente.
Stull a introduit le concept de matrice de ``transilience",
matrice contenant les taux d'échange d'air entre les
différentes mailles d'une colonne atmosphérique.
Le coefficient ![]() de la matrice est par exemple la concentration
massique
dans la maille
de la matrice est par exemple la concentration
massique
dans la maille ![]() au temps
au temps ![]() d'un traceur passif injecté
uniformément dans la maille
d'un traceur passif injecté
uniformément dans la maille ![]() au temps
au temps ![]() en quantité unitaire.
Plus que d'une paramétrisation, il s'agit en fait d'un cadre formel dans
lequel développer une paramétrisation.
Dans ce formalisme, la diffusion turbulente sera représentée par une
matrice d'échange tridiagonale (en un pas de temps, une maille n'échange
qu'avec les mailles immédiatement au-dessus et au-dessous).
en quantité unitaire.
Plus que d'une paramétrisation, il s'agit en fait d'un cadre formel dans
lequel développer une paramétrisation.
Dans ce formalisme, la diffusion turbulente sera représentée par une
matrice d'échange tridiagonale (en un pas de temps, une maille n'échange
qu'avec les mailles immédiatement au-dessus et au-dessous).
Stull et ses collaborateurs ont analysé les résultats de simulations
des grands tourbillons en termes de matrices de transilience.
Les résultats montrés sur la Fig. 3.13 ont été obtenus
pour une simulation des grands tourbillons
d'un cas académique de couche limite convective similaire aux simulations
de Moeng et Sullivan (1994) décrites plus haut.
Dans ce cas particulier, le temps caractéristique d'advection par
les thermiques, ![]() , est de l'ordre de 18 minutes.
Pour calculer les matrices, on commence par intégrer le modèle sans
traceurs jusqu'à atteindre un état de régime de la turbulence. On
introduit alors un traceur uniformément dans chaque couche du modèle.
Après un certain temps, on peut tracer le profil vertical
moyen de la concentration de ce traceur. Les matrices de transilience
associées, avec en abcisse la couche d'origine et en ordonnée la couche
d'arrivée du traceur, sont montrées sur la Fig. 3.13,
ainsi que l'interprétation physique de la forme
de la matrice, en haut à gauche.
Au-dessus de 1,2
, est de l'ordre de 18 minutes.
Pour calculer les matrices, on commence par intégrer le modèle sans
traceurs jusqu'à atteindre un état de régime de la turbulence. On
introduit alors un traceur uniformément dans chaque couche du modèle.
Après un certain temps, on peut tracer le profil vertical
moyen de la concentration de ce traceur. Les matrices de transilience
associées, avec en abcisse la couche d'origine et en ordonnée la couche
d'arrivée du traceur, sont montrées sur la Fig. 3.13,
ainsi que l'interprétation physique de la forme
de la matrice, en haut à gauche.
Au-dessus de 1,2 ![]() , l'air est très peu affecté par la turbulence.
Seuls les termes diagonaux sont donc non nuls.
Au bout d'un temps
, l'air est très peu affecté par la turbulence.
Seuls les termes diagonaux sont donc non nuls.
Au bout d'un temps ![]() , l'air de la partie haute de la
couche limite est descendu lentement ce qui donne de grands termes
juste en dessous de la diagonale. A l'opposé, on voit sur
la gauche de la matrice que l'air provenant de la couche de surface
se répartit rapidement dans la couche mélangée. A
, l'air de la partie haute de la
couche limite est descendu lentement ce qui donne de grands termes
juste en dessous de la diagonale. A l'opposé, on voit sur
la gauche de la matrice que l'air provenant de la couche de surface
se répartit rapidement dans la couche mélangée. A ![]() , l'air de la couche
de surface se retrouve principalement en haut de la couche mélangée.
A la fois à
, l'air de la couche
de surface se retrouve principalement en haut de la couche mélangée.
A la fois à ![]() et
et ![]() , la matrice de transilience est fortement
asymétrique.
A
, la matrice de transilience est fortement
asymétrique.
A ![]() , l'air a eu le temps de bien se mélanger et la matrice prend
alors une forme plus symétrique, avec des coefficients relativement uniformes
dans la couche limite : de l'air originaire de la couche limite se retrouve
à peu près équi-réparti dans la couche limite au bout de
, l'air a eu le temps de bien se mélanger et la matrice prend
alors une forme plus symétrique, avec des coefficients relativement uniformes
dans la couche limite : de l'air originaire de la couche limite se retrouve
à peu près équi-réparti dans la couche limite au bout de ![]() .
.
La seule fermeture à proprement parler qui semble avoir été proposée dans le cadre des matrices de transilience est le modèle asymétrique de Pleim et Chang (1992). Dans ce modèle, une forme particulière est imposée à la matrice pour rendre compte de l'opposition entre les ascendances thermiques plus concentrées et les subsidences plus lentes. La première couche au-dessus de la surface échange de l'air avec toutes les mailles situées au-dessus tandis que toutes les autres mailles transfèrent de l'air à la maille immédiatement en dessous. On illustre le principe de cette paramétrisation sur la Fig. 3.14. Cette paramétrisation permet d'obtenir un transport de chaleur remontant le gradient de température potentielle, sans autre traitement, dés lors que la première couche du modèle est plus chaude (en température potentielle) que les couches au-dessus.
La dernière catégorie d'approches, celle à laquelle se rattache le modèle du thermique présenté ci-après, est la catégorie des modèles en flux de masse.
Les approches en flux de masse remontent aux travaux de Lilly (1968) et Arakawa et Schubert (1974) et étaient principalement motivées à leur origine par la paramétrisation des mouvements dans les cumulus.
On entend de façon générale par "flux de masse" une approche qui tend à expliciter le transport vertical par des mouvement (ou flux de masse) dans des sous colonnes de la colonne atmosphérique.
Les schémas de Tiedtke (1989) et Emanuel (1991) appartiennent tous les deux à cette catégorie des schémas en flux de masse.
Dans le schéma de Tiedtke, on isole par exemple trois sous colonnes,
une pour les ascendances rapides (au c![]() ur des nuages convectifs), une
pour les descentes précipitantes (entretenues par l'évaporation des
précipitations) et une pour l'environnement.
Dans les panaches ascendants et descendants, on calcule explicitement
la température, l'eau etc... à chaque niveau, sous des hypothèses de
stationnarité, pour ensuite calculer le bilan total dans la colonne.
ur des nuages convectifs), une
pour les descentes précipitantes (entretenues par l'évaporation des
précipitations) et une pour l'environnement.
Dans les panaches ascendants et descendants, on calcule explicitement
la température, l'eau etc... à chaque niveau, sous des hypothèses de
stationnarité, pour ensuite calculer le bilan total dans la colonne.
Dans le cadre de l'étude de la couche limite et de la convection peu profonde, le concept des flux de masse a été beaucoup utilisé d'une façon relativement différente, en développant en général des modélisations simple à fin d'analyse plutôt que de simulation proprement dite, en utilisant une idéalisation des profils verticaux. Ces approches remontent aux travaux de Betts (1973).
Dans ces approches, la couche limite convective est décrite en une ou quelques couches dans les quelles ont suppose que les quantités physiques sont bien mélangées, et des couches infiniment fines de transition au travers des quelles les différentes variables subissent des discontinuités.
Pour une couche limite sèche comme celle décrite plus haut, on aura typiquement une discontinuité de température en surface, une température potentielle unique sur toute la hauteur de la couche limite, une nouvelle discontinuité au niveau de l'inversion, pour se raccorder au profil de la troposphère libre.
Le schéma développé ici s'appuie sur une vue idéalisée d'une cellule convective ou d'un thermique proche de celle présentée plus haut.
Considérons un profil de température potentielle typique de la couche limite convective avec une couche de surface (CS sur la Fig. 3.15) instable (typiquement de une à quelques centaines de mètres d'épaisseur), une couche mélangée (CM sur la Fig. 3.15) neutre, surmontée d'une zone stable (couche d'entraînement plus troposphère libre).
Dans cet environnement idéalisé, le thermique est vu comme un
panache d'air chaud montant de la couche de surface
sous l'effet de sa flottabilité.
On suppose que l'air dans le
thermique conserve sa température potentielle virtuelle
qui est donc celle de la couche de surface,
![]() .3.5
.3.5
On suppose de plus que le mouvement dans le panache est stationnaire
et sans friction, que la vapeur d'eau ne condense pas et que l'air
monte sous le seul effet de sa flottabilité. Dans ce cas, l'accélération
verticale de l'air, dans le thermique, s'écrit
| (3.62) |
| (3.63) |
Pour calculer le transport convectif, il faut en fait calculer
le flux de masse par unité de surface
![]() où
où ![]() est la fraction de la surface horizontale
couverte par des panaches ascendants (on parlera de couverture fractionnaire).
Dans un premier temps, on va supposer que le flux de masse
est la fraction de la surface horizontale
couverte par des panaches ascendants (on parlera de couverture fractionnaire).
Dans un premier temps, on va supposer que le flux de masse ![]() ne dépend
pas de l'altitude (panache conservatif) et on va essayer de déterminer
ce flux. Pour cela, il est nécessaire de rentrer un peu plus en détail dans
la description de la géométrie du thermique.
ne dépend
pas de l'altitude (panache conservatif) et on va essayer de déterminer
ce flux. Pour cela, il est nécessaire de rentrer un peu plus en détail dans
la description de la géométrie du thermique.
On va considérer ici la configuration en rouleau, plus simple à analyser,
c'est à dire une situation où on a une direction horizontale
invariante, par exemple selon l'axe ![]() . L'ascendance est alimentée par
convergence horizontale dans la couche de surface. Si les effets de friction
et de rotation sont négligés, et si on suppose que l'écoulement est stationnaire
on a
. L'ascendance est alimentée par
convergence horizontale dans la couche de surface. Si les effets de friction
et de rotation sont négligés, et si on suppose que l'écoulement est stationnaire
on a
| (3.64) |
| (3.65) |
| (3.66) |
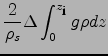 |
(3.67) | ||
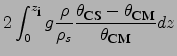 |
(3.68) |
D'autre part,
en géométrie bidimensionnelle, le flux vertical dans le thermique doit être égal
à la convergence horizontale dans la couche de surface :
| (3.69) |
Le fait que les vitesses maximales horizontale et verticale soient du
même ordre de grandeur implique en retour que la distance ![]() entre la subsidence et l'ascendance est de l'ordre de 1.
En effet, si la largeur de la cellule
entre la subsidence et l'ascendance est de l'ordre de 1.
En effet, si la largeur de la cellule ![]() était beaucoup plus grande que
sa hauteur, une particule partant de la distance
était beaucoup plus grande que
sa hauteur, une particule partant de la distance ![]() atteindrait le sommet
de la couche limite avant d'atteindre le panache ascendant et créerait
ainsi une ascendance secondaire.
Cette isotropie est effectivement observée dans les expériences de
Rayleigh-Benard. Dans la paramétrisation, le rapport
atteindrait le sommet
de la couche limite avant d'atteindre le panache ascendant et créerait
ainsi une ascendance secondaire.
Cette isotropie est effectivement observée dans les expériences de
Rayleigh-Benard. Dans la paramétrisation, le rapport
![]() est utilisé comme paramètre libre. La couverture fractionnaire
est minimum au niveau
est utilisé comme paramètre libre. La couverture fractionnaire
est minimum au niveau
![]() où elle vaut
où elle vaut
![]() . On en tire une relation de fermeture
pour le calcul du flux de masse dans l'ascendance :
. On en tire une relation de fermeture
pour le calcul du flux de masse dans l'ascendance :
On a supposé jusqu'ici que le flux de masse était constant dans le thermique.
Cette hypothèse conduit à une couverture fractionnaire
infinie au sommet de la couche limite,
là où ![]() est nul.
En pratique, ceci signifie que le thermique ne peut pas rester à flux constant
et qu'il doit restituer son air dans l'environnement.
Pour la paramétrisation, on suppose que, au-dessus de l'inversion, la largeur
du thermique décroît pour s'annuler à
est nul.
En pratique, ceci signifie que le thermique ne peut pas rester à flux constant
et qu'il doit restituer son air dans l'environnement.
Pour la paramétrisation, on suppose que, au-dessus de l'inversion, la largeur
du thermique décroît pour s'annuler à
![]() (en pratique on teste ci-dessous
une décroissance linéaire et une décroissance quadratique).
(en pratique on teste ci-dessous
une décroissance linéaire et une décroissance quadratique).
En plus, on permet que l'air soit détraîné du thermique sous l'effet du
mélange turbulent en dessous de l'inversion. Ce détraînement est pris
en compte sous forme d'un épluchage du thermique.
Une analyse d'échelle montre que l'épaisseur de la couche limite d'un jet
pénétrant dans un environnement au repos se développe en
![]() (voir par exemple Prandtl et Tietjens, 1934, Ch.IV).
Dans notre cas,
(voir par exemple Prandtl et Tietjens, 1934, Ch.IV).
Dans notre cas,
![]() où
où ![]() est la viscosité turbulente du gaz.
Pour une vitesse typique de 1 m/s et une viscosité turbulente de
10 m
est la viscosité turbulente du gaz.
Pour une vitesse typique de 1 m/s et une viscosité turbulente de
10 m![]() s
s![]() ,
, ![]() m.
On retient cette formulation pour réduire la section
du thermique en dessous de
m.
On retient cette formulation pour réduire la section
du thermique en dessous de
![]() , en considérant
, en considérant ![]() comme un paramètre
ajustable.
comme un paramètre
ajustable.
La présentation précédente partait d'un profil de température idéalisé,
avec notamment une température potentielle constante dans la couche mélangée.
Dans la formulation complète, qui doit pouvoir être utilisée pour un profil
de température quelconque, le thermique est encore caractérisé par
sa vitesse verticale (![]() ), sa température potentielle
(
), sa température potentielle
(![]() ) et la couverture fractionnaire des thermiques (
) et la couverture fractionnaire des thermiques (![]() ).
Le flux de masse dans les ascendances est
).
Le flux de masse dans les ascendances est
![]() (
(![]() est supposé identique à l'intérieur et à l'extérieur du thermique).
Notons
est supposé identique à l'intérieur et à l'extérieur du thermique).
Notons
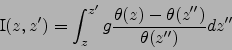 |
(3.71) |
Le flux de masse ![]() est relié au flux d'air entrant
est relié au flux d'air entrant ![]() et au flux d'air
détraîné
et au flux d'air
détraîné ![]() par :
par :
| (3.73) |
| (3.74) |
| (3.75) |
Le niveau de l'inversion
![]() est défini comme l'altitude où la température
à l'intérieur du thermique
est défini comme l'altitude où la température
à l'intérieur du thermique ![]() devient plus petite que celle de l'environnement
(début de l'overshoot).
On calcule alors les propriétés de l'air à l'intérieur du thermique
suivant l'équation de conservation
devient plus petite que celle de l'environnement
(début de l'overshoot).
On calcule alors les propriétés de l'air à l'intérieur du thermique
suivant l'équation de conservation
| (3.77) |
Pour le transport de la quantité de mouvement, l'idée la plus simple consiste
à traiter les deux composantes horizontales ![]() et
et ![]() comme des scalaires.
C'est cette approche qui est retenue dans la version standard.
On teste aussi une version dans laquelle on inclut un échange de quantité
de mouvement par les forces de pression exercées
entre le thermique et l'environnement. Cet échange
va tendre à incliner le thermique dont la vitesse horizontale va progressivement
s'approcher de celle de l'environnement.
Pour ce test, on utilise la géométrie tridimensionnelle et on applique la formule utilisée
pour calculer par exemple la traînée d'un ballon dans l'atmosphère.
Cette traînée s'exprime comme le produit du carré du vent apparent par
la section apparente et un coefficient de traînée. Dans la géométrie tridimensionnelle, la
section apparente du thermique est
comme des scalaires.
C'est cette approche qui est retenue dans la version standard.
On teste aussi une version dans laquelle on inclut un échange de quantité
de mouvement par les forces de pression exercées
entre le thermique et l'environnement. Cet échange
va tendre à incliner le thermique dont la vitesse horizontale va progressivement
s'approcher de celle de l'environnement.
Pour ce test, on utilise la géométrie tridimensionnelle et on applique la formule utilisée
pour calculer par exemple la traînée d'un ballon dans l'atmosphère.
Cette traînée s'exprime comme le produit du carré du vent apparent par
la section apparente et un coefficient de traînée. Dans la géométrie tridimensionnelle, la
section apparente du thermique est
![]() . Il faut diviser le
terme de traînée par
. Il faut diviser le
terme de traînée par ![]() pour se ramener à une force par unité de surface
horizontale de sorte qu'on obtient finalement
pour se ramener à une force par unité de surface
horizontale de sorte qu'on obtient finalement
| (3.79) |
Le transport total d'une variable ![]() est finalement donné
par la somme du transport vers le haut dans le thermique et du transport
vers le bas dans l'environnement avec un flux compensatoire
est finalement donné
par la somme du transport vers le haut dans le thermique et du transport
vers le bas dans l'environnement avec un flux compensatoire ![]()
| (3.80) |
Une approximation supplémentaire est finalement introduite pour rendre
le schéma plus robuste. En effet,
si on intègre telle quelle l'Eq. 3.76, on peut aboutir à des valeurs
aberrantes de ![]() . Considérons l'exemple d'un traceur initialement
confiné dans la couche de surface dans une situation convective.
L'Eq. 3.76 prédirait
. Considérons l'exemple d'un traceur initialement
confiné dans la couche de surface dans une situation convective.
L'Eq. 3.76 prédirait
![]() dans la couche mélangée alors qu'on a
dans la couche mélangée alors qu'on a
![]() de sorte
qu'on aurait
de sorte
qu'on aurait ![]() . Ce problème provient de l'hypothèse de stationnarité,
hypothèse
qu'on n'a pas envie de faire tomber, en particulier pour des raisons de
simplicité. Une alternative consiste à assimiler l'environnement et
les grandeurs moyennes (
. Ce problème provient de l'hypothèse de stationnarité,
hypothèse
qu'on n'a pas envie de faire tomber, en particulier pour des raisons de
simplicité. Une alternative consiste à assimiler l'environnement et
les grandeurs moyennes (
![]() ). Cette approximation qui est valide
pour
). Cette approximation qui est valide
pour
![]() , est en général utilisée dans les schémas de convection
profonde. Elle est moins évidente dans notre cas où la couverture
fractionnaire des ascendances est typiquement comprise entre 5 et
30
, est en général utilisée dans les schémas de convection
profonde. Elle est moins évidente dans notre cas où la couverture
fractionnaire des ascendances est typiquement comprise entre 5 et
30 ![]() .
Cette nouvelle approximation est validée a posteriori par le bon comportement
de la paramétrisation quand on la compare à des simulations des grands
tourbillons.
.
Cette nouvelle approximation est validée a posteriori par le bon comportement
de la paramétrisation quand on la compare à des simulations des grands
tourbillons.
Le schéma dépend finalement de 4 paramètres ajustables.
Pour choisir la valeur du rapport d'aspect ![]() on se base sur les observations dans les
configurations en rouleaux. Le paramètre
on se base sur les observations dans les
configurations en rouleaux. Le paramètre ![]() est fixé à 0 par soucis
de simplicité. Finalement, les paramètres relatifs au détraînement
sont ajustés pour obtenir un bon accord avec les résultats de
simulations des grands tourbillons
présentés dans la section suivante. Bien que différentes combinaisons soient
possibles, nous retenons
est fixé à 0 par soucis
de simplicité. Finalement, les paramètres relatifs au détraînement
sont ajustés pour obtenir un bon accord avec les résultats de
simulations des grands tourbillons
présentés dans la section suivante. Bien que différentes combinaisons soient
possibles, nous retenons
![]() m et
m et ![]() .
.
La discrétisation des équations est donnée par Hourdin et al. (2002).
La description ci-dessus ne traite que de la partie méso-échelle du transport de couche limite. Le mélange de petite échelle, important notamment dans la couche de surface, doit être traité avec une autre paramétrisation. Dans les tests montrés par la suite, on utilise pour ces échelles soit la paramétrisation d'origine du modèle du LMD soit celle de Mellor et Yamada. Comme on le verra par la suite, ces paramétrisations en diffusion turbulente, sensées à l'origine traiter l'ensemble de la turbulence de couche limite, voient leur rôle se cantonner naturellement à la couche de surface une fois la paramétrisation du thermique activée, cette dernière stabilisant le profil de température dans la couche mélangée.
Un traitement spécial doit également être appliqué pour les couches limites
nocturnes. Les formulations classiques en énergie cinétique turbulente
sont connues pour s'effondrer en conditions très stables.
Les tests effectués plus loin pour des cas de fort cycle diurne continental
confirment ce point.
En l'absence de traitement spécifique, on observe la nuit un découplage
de la surface et de la première couche d'atmosphère.
Pour pallier ce problème, on adopte une formule citée dans un certain nombre
de travaux et qui dit que la hauteur de la couche limite doit être
au moins égale à
![]() où
où ![]() est le facteur de Coriolis
en s
est le facteur de Coriolis
en s![]() .
Cette formule ayant la fâcheuse propriété d'être singulière à l'équateur,
on prend arbitrairement
.
Cette formule ayant la fâcheuse propriété d'être singulière à l'équateur,
on prend arbitrairement ![]() s
s![]() .
On en déduit une estimation d'un coefficient de diffusion turbulente minimum
.
On en déduit une estimation d'un coefficient de diffusion turbulente minimum
![]() .
.
Pour valider la nouvelle paramétrisation, on se base tout d'abord sur des résultats de simulations des grands tourbillons. L'avantage d'utiliser des résultats de simulations des grands tourbillons plutôt que des observations réside dans le fait que les conditions expérimentales sont connues exactement et peuvent être modifiées, ainsi que dans la plus grande facilité d'accès à des diagnostics spécifiques.
Ici, on a retenu les résultats de simulations des grands tourbillons utilisées par Ayotte et al. (1996) dans une étude d'intercomparaison de paramétrisations de la couche limite en conditions neutres ou convectives.
On ne donne ici qu'une description succincte des simulations qui sont décrites en détail par Ayotte et al. (1996). Le code utilisé a été développé à l'origine par Moeng (1984). Il est pseudo-spectral sur l'horizontale et en différences finies sur la verticale. Le domaine est supposé périodique horizontalement. La paramétrisation des tourbillons sous-mailles repose sur une équation pronostique de l'énergie cinétique turbulente.
Les simulations sont effectuées dans des conditions sèches et
pour des profils de température neutres ou instables, avec un flux
de chaleur prescrit en surface
![]() .
Neuf simulations, 00WC, 05WC, 00SC, 03SC, 05SC, 24SC, 24F, 15B, 24B,
sont utilisées. Elle diffèrent d'abord par la valeur du flux de
chaleur en surface
(le 05 de 05SC correspond par exemple à
.
Neuf simulations, 00WC, 05WC, 00SC, 03SC, 05SC, 24SC, 24F, 15B, 24B,
sont utilisées. Elle diffèrent d'abord par la valeur du flux de
chaleur en surface
(le 05 de 05SC correspond par exemple à
![]() 0,05 K m s
0,05 K m s![]() )
et par le profil initial de température potentielle.
Les simulations WC (weakly caped) présentent une inversion peu marquée en
sommet de couche limite contrairement aux cas SC (strongly caped).
Pour les simulations SC et WC, on impose un vent géostrophique constant
de 15 m s
)
et par le profil initial de température potentielle.
Les simulations WC (weakly caped) présentent une inversion peu marquée en
sommet de couche limite contrairement aux cas SC (strongly caped).
Pour les simulations SC et WC, on impose un vent géostrophique constant
de 15 m s![]() suivant
suivant ![]() .
La simulation 24F (Free) correspond à un cas de convection libre sans
forçage géostrophique alors que les cas 15B et 24B (Baroclines) correspondent
à un vent géostrophique de 10 m s
.
La simulation 24F (Free) correspond à un cas de convection libre sans
forçage géostrophique alors que les cas 15B et 24B (Baroclines) correspondent
à un vent géostrophique de 10 m s![]() suivant
suivant ![]() et variant
de 0 en surface à 20 m s
et variant
de 0 en surface à 20 m s![]() à 2000 m suivant
à 2000 m suivant ![]() .
Les simulations 24SC et 05SC correspondent à peu près aux simulations
B et SB de l'article de Moeng et Sullivan (1994) dont les résultats sont montrés
sur la Fig. 3.4.
.
Les simulations 24SC et 05SC correspondent à peu près aux simulations
B et SB de l'article de Moeng et Sullivan (1994) dont les résultats sont montrés
sur la Fig. 3.4.
Toutes les simulations sont initialisées à partir de champs homogènes
horizontalement auxquels on ajoute des petites perturbations
aléatoires.
Une première simulation est effectuée sur une période de 5 ![]() où
où
![]() est un temps caractéristique (l'échelle de temps convective de l'ordre
de 500 à 1000 s pour les simulations avec un flux non nul en surface).
L'état final de cette première simulation est alors utilisé pour initialiser
les simulations des grands tourbillons et les simulations uni-colonnes au temps
est un temps caractéristique (l'échelle de temps convective de l'ordre
de 500 à 1000 s pour les simulations avec un flux non nul en surface).
L'état final de cette première simulation est alors utilisé pour initialiser
les simulations des grands tourbillons et les simulations uni-colonnes au temps ![]() .
Les analyses présentées ci-dessous portent sur la période
.
Les analyses présentées ci-dessous portent sur la période
![]() .
.
En plus des variables météorologiques, deux traceurs sont pris en compte
dans les simulations des grands tourbillons. Les deux sont initialisés au temps ![]() avec une
discontinuité à l'inversion comme suit:
avec une
discontinuité à l'inversion comme suit:
| (3.81) | |||
| (3.82) |
Le traceur C est uniquement transporté alors que le traceur B, un analogue à la vapeur d'eau dans l'idée des auteurs, est en plus forcé par un flux en surface. Ce flux est calculé en fonction du contraste entre la concentration dans l'atmosphère au-dessus du sol et une valeur de surface de 15 (unités arbitraires).
Pour ces différentes simulations, l'auteur de l'étude - retrouvé au fil de la toile derrière les rangées d'éoliennes qu'il commercialise en Australie - nous a gracieusement communiqué les profils de début et de fin des simulations des grands tourbillons. Nous disposons à la fois des moyennes des différentes variables du modèle et des moyennes des termes croisés (variances et covariances). En revanche, il n'a pas été possible de récupérer ou de recalculer d'autres grandeurs qui auraient pourtant été intéressantes pour la validation de la paramétrisation tels les moments d'ordre 3 ou les facteurs d'asymétrie.
On compare les résultats des simulations de Ayotte et al. (1996) avec
les résultats d'une version uni-colonne du modèle LMDZ.
Dans le modèle uni-colonne, restreint aux processus de couche limite,
l'équation donnant
l'évolution temporelle des variables ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() peut s'écrire de façon générique
peut s'écrire de façon générique
| (3.83) |
Le flux de surface est prescrit pour le traceur ![]() (il est nul) et pour
la température potentielle. Pour les vents et le traceur
(il est nul) et pour
la température potentielle. Pour les vents et le traceur ![]() , la condition
en surface suit les relations de similitude de Businger-Dyer :
, la condition
en surface suit les relations de similitude de Businger-Dyer :
| (3.84) |
| (3.85) |
Au sein de l'atmosphère, le flux turbulent dans les différents jeux
de paramétrisations testés
peut s'écrire de façon générique comme
| (3.86) |
On compare différentes paramétrisations de la couche limite.
Les simulations sont effectuées avec la grille verticale des simulations des grands tourbillons, avec une taille de mailles de 10 ou 20 m suivant les cas. Suivant le cas également, le pas de temps varie entre 15 et 100 s.
|
Sur la Fig. 3.16, on commence par montrer
les profils verticaux de température potentielle,
de flux de chaleur, de traceurs et de vents pour 4 cas,
à la fois pour les simulations des grands tourbillons et pour le modèle du thermique dans sa configuration
nominale (MY+TH avec ![]() m,
m, ![]() ,
, ![]() et
et ![]() ).
On montre les profils initiaux ainsi que les moyennes entre
).
On montre les profils initiaux ainsi que les moyennes entre
![]() et
et
![]() .
.
L'accord apparemment très bon entre la paramétrisation et les simulations des grands tourbillons est dû pour une grande part au forçage très contraignant de ces simulations académiques. Comme on l'a expliqué plus haut, avec un un flux de chaleur prescrit en surface et une température homogène dans la couche mélangée, le modèle est essentiellement contraint à chauffer uniformément la couche mélangée et le flux ne peut donc que décroître à peu près uniformément depuis la surface jusqu'à l'inversion.
|
|
|
|
|
|
Les Fig. 3.17 et 3.18 montrent les résultats pour les cas 05WC et 24SC pour les paramétrisations de HB et MY. La paramétrisation de HB se comporte globalement bien dans ce type de conditions (Ayotte et al., 1996). Cette paramétrisation a cependant tendance à exagérer l'inversion. Elle surestime aussi l'entraînement en sommet de couche limite dans le cas 05WC alors qu'elle le sous-estime légèrement pour le cas 24SC. Le schéma de MY sous-estime systématiquement l'entraînement. A noter que le bon accord relatif pour le flux n'est obtenu dans ce cas que grâce à une déstabilisation du profil de température potentielle sans laquelle on ne peut avoir un flux vers le haut. Les figures 3.19, 3.20, 3.21 et 3.22, correspondant respectivement aux simulations LMD, LMD+CG, LMD+AJS et LMD+TH, illustrent l'importance du traitement des aspects non locaux. La paramétrisation du LMD sans aucun traitement aboutit à des atmosphères très instables avec peu d'entraînement au sommet dans le cas 24SC. L'introduction d'un contre-gradient (LMD+CG) résout seulement en partie le problème. Le contre-gradient, imposé ici indépendamment de l'intensité de l'instabilité, est trop fort dans le cas 05WC mais trop faible pour 24SC. L'ajustement sec (LMD+AJS) améliore d'une certaine façon les profils de température potentielle mais sans affecter beaucoup l'entraînement des traceurs en sommet de couche limite. En revanche, l'activation du modèle du thermique (LMD+TH) conduit à des résultats très proches de MY+TH.
Afin de quantifier cette intercomparaison, nous retenons les
diagnostics proposés par Ayotte et al. (1996) et qui se concentrent sur
l'entraînement en sommet de couche limite. En particulier, ils proposent
de calculer pour un scalaire ![]() (
(![]() , B ou C), le coefficient
, B ou C), le coefficient
![$\displaystyle - \frac{1}{t_f-t_1}\int_{z_i(t_0)}^H \left[\phi(z,t_f)-\phi(z,t_0)\right] dz$](img824.png) |
|||
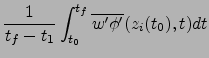 |
(3.87) |
|
|
Sur la Fig. 3.23 on montre, pour les neuf cas étudiés
par Ayotte et al. (1996), le coefficient ![]() pour les
simulations des grands tourbillons, pour le modèle du thermique et pour les schémas de HB et MY.
La paramétrisation de MY tend à sous-estimer systématiquement l'entraînement.
Le schéma de HB surestime l'entraînement pour le cas 05WC et et le
sous-estime pour les autres cas.
Les deux schémas ne réussissent pas à prédire un entraînement significatif
dans le cas de convection libre.
Dans l'intercomparaison de Ayotte et al. (1996), on retrouve le même comportement
pour tous les schémas testés sauf pour un modèle de ``couche mélangée" qui
tend, lui, à surestimer systématiquement l'entraînement.
L'accord avec les simulations des grands tourbillons est généralement meilleur pour le modèle du thermique
pour les coefficients
pour les
simulations des grands tourbillons, pour le modèle du thermique et pour les schémas de HB et MY.
La paramétrisation de MY tend à sous-estimer systématiquement l'entraînement.
Le schéma de HB surestime l'entraînement pour le cas 05WC et et le
sous-estime pour les autres cas.
Les deux schémas ne réussissent pas à prédire un entraînement significatif
dans le cas de convection libre.
Dans l'intercomparaison de Ayotte et al. (1996), on retrouve le même comportement
pour tous les schémas testés sauf pour un modèle de ``couche mélangée" qui
tend, lui, à surestimer systématiquement l'entraînement.
L'accord avec les simulations des grands tourbillons est généralement meilleur pour le modèle du thermique
pour les coefficients ![]() ainsi que pour la température de l'air près de la
surface (dernier panneau de la Fig. 3.23).
ainsi que pour la température de l'air près de la
surface (dernier panneau de la Fig. 3.23).
Sur la Fig. 3.24, on voit que la couche limite du LMD tend à surestimer l'entraînement pour les cas intermédiaires (00SC, 03SC et 05SC). Cette surestimation est peu sensible au traitement des aspects non locaux. Pour les cas très convectifs, seul le modèle du thermique arrive à effectuer un transport raisonnable. A nouveau, l'entraînement calculé avec LMD+TH est très proche de celui obtenu avec MY+TH (excepté dans les cas intermédiaires pour la température potentielle ou on conserve la surestimation par le modèle du LMD).
|
Comme on l'a dit plus haut, les résultats des simulations des grands tourbillons ont été utilisés pour
sélectionner les valeurs nominales des paramètres pour le détraînement.
La figure Fig. 3.25 montre le paramètre ![]() pour la température potentielle
et le traceur B et pour différentes valeurs des paramètres
(
pour la température potentielle
et le traceur B et pour différentes valeurs des paramètres
(![]() m,
m, ![]() m,
m, ![]() 5 et
5 et ![]() ).
Quand on augmente
).
Quand on augmente ![]() , on diminue
, on diminue ![]() dans les cas convectifs.
A l'opposé, sans épluchage en dessous de l'inversion (
dans les cas convectifs.
A l'opposé, sans épluchage en dessous de l'inversion (![]() ),
ou quand on utilise une décroissance moindre au-dessus de l'inversion
(
),
ou quand on utilise une décroissance moindre au-dessus de l'inversion
(![]() ), l'entraînement est surestimé.
Cependant, une simulation avec
), l'entraînement est surestimé.
Cependant, une simulation avec ![]() m et
m et ![]() produit un accord
avec les simulations des grands tourbillons aussi bon que le cas nominal.
L'entraînement est relativement peu sensible au rapport d'aspect
produit un accord
avec les simulations des grands tourbillons aussi bon que le cas nominal.
L'entraînement est relativement peu sensible au rapport d'aspect ![]() .
Enfin, quand on prend en compte l'échange de quantité de mouvement entre
le thermique et l'environnement (
.
Enfin, quand on prend en compte l'échange de quantité de mouvement entre
le thermique et l'environnement (![]() ), on ne modifie pas non plus
beaucoup l'entraînement.
), on ne modifie pas non plus
beaucoup l'entraînement.
Pour finir, remarquons que, même pour des valeurs des paramètres assez
éloignées des valeurs nominales, le modèle du thermique conserve une bonne
sensibilité aux flux de surface et aux profils initiaux. Par exemple,
pour ![]() , le coefficient pour
, le coefficient pour ![]() est toujours un peu plus grand
pour le cas 24F que pour le cas 24SC;
est toujours un peu plus grand
pour le cas 24F que pour le cas 24SC; ![]() est aussi systématiquement plus
grand pour le cas 05SC que pour le cas 05WC.
Enfin, pour le traceur
est aussi systématiquement plus
grand pour le cas 05SC que pour le cas 05WC.
Enfin, pour le traceur ![]() , les résultats sont encore moins sensibles aux
paramètres du modèle (les résultats sont similaires pour
, les résultats sont encore moins sensibles aux
paramètres du modèle (les résultats sont similaires pour ![]() ).
).
|
La Fig. 3.26 montre la structure du thermique telle qu'elle est simulée avec la paramétrisation nominale ainsi que la décomposition du flux de chaleur entre la partie du thermique à proprement parler (courbe fine) et la partie diffuse paramétrisée avec le schéma de MY (courbe pointillée). La chaleur est d'abord transférée dans la couche de surface par le schéma de MY puis répartie dans la couche limite par le thermique. Dans la couche mélangée, le thermique transporte la chaleur vers le haut malgré une atmosphère légèrement stable.
A remarquer que, quand elle est utilisée seule, la paramétrisation de MY est active également dans la couche mélangée du fait de la déstabilisation du profil de température.
Les thermiques couvrent environ 10![]() de la surface.
On obtient des valeurs similaires pour les autres cas.
A noter que le bon accord en termes d'entraînement qu'on obtient
avec
de la surface.
On obtient des valeurs similaires pour les autres cas.
A noter que le bon accord en termes d'entraînement qu'on obtient
avec ![]() correspond à des couvertures beaucoup plus faibles (3-5
correspond à des couvertures beaucoup plus faibles (3-5![]() ).
Ces valeurs sont en accord avec les analyses des simulations des grands tourbillons (Moeng et Sullivan, 1994)
(qui montrent des fractions de 10-20
).
Ces valeurs sont en accord avec les analyses des simulations des grands tourbillons (Moeng et Sullivan, 1994)
(qui montrent des fractions de 10-20![]() avec un rapport d'aspect de 2-3).
Les mesures avions dans des conditions similaires conduisent à des résultats
semblables (Williams et Hacker, 1993).
Les valeurs sont cependant dans la tranche basse des observations ce qui peut
être relié au fait que nous ne considérons comme ascendance que l'air
qui provient directement de la couche de surface sous l'effet de sa flottabilité.
avec un rapport d'aspect de 2-3).
Les mesures avions dans des conditions similaires conduisent à des résultats
semblables (Williams et Hacker, 1993).
Les valeurs sont cependant dans la tranche basse des observations ce qui peut
être relié au fait que nous ne considérons comme ascendance que l'air
qui provient directement de la couche de surface sous l'effet de sa flottabilité.
|
La comparaison des moments d'ordre 2 aux résultats des simulations des grands tourbillons permet de mieux comprendre le comportement de la paramétrisation et la physique de la couche limite convective.
Cette comparaison pour les cas 05WC et 24SC est montrée sur la Fig. 3.27.
Dans les résultats de simulations des grands tourbillons fournis par Ayotte (courbes épaisses),
les moments d'ordre deux contiennent la partie explicite
plus la partie paramétrisée pour le vent et seulement la partie explicite
pour la température.
Pour la paramétrisation, on montre à la fois la contribution des thermiques
(tiretés)
| (3.88) | |||
| (3.89) |
Dans la couche de surface, les fluctuations de vent et de température
sont bien reproduites. La légère surestimation de
![]() est sans doute due au fait que les résultats des simulations des grands tourbillons n'incluent pas la
partie paramétrisée.
est sans doute due au fait que les résultats des simulations des grands tourbillons n'incluent pas la
partie paramétrisée.
Dans la couche mélangée, pour
![]() , la prédiction de
, la prédiction de
![]() par le modèle du thermique est aussi très proche
des résultats des simulations des grands tourbillons. En revanche,
par le modèle du thermique est aussi très proche
des résultats des simulations des grands tourbillons. En revanche,
![]() est sous-évalué d'un facteur 2 environ.
Ceci peut se comprendre de la façon suivante. Dans la couche mélangée, nous tenons
compte seulement de la partie liée aux structures méso-échelles, en nous
basant sur une vue idéalisée d'un thermique homogène en vent et en température
comme l'illustrent les graphes du haut de la Fig. 3.28.
Dans la réalité, l'air dans le thermique (et dans l'environnement mais
dans une moindre mesure) est également turbulent à plus petite échelle.
Cependant, comme on l'a dit plus haut,
les fluctuations de température associées avec ces fluctuations
de petite échelle de
est sous-évalué d'un facteur 2 environ.
Ceci peut se comprendre de la façon suivante. Dans la couche mélangée, nous tenons
compte seulement de la partie liée aux structures méso-échelles, en nous
basant sur une vue idéalisée d'un thermique homogène en vent et en température
comme l'illustrent les graphes du haut de la Fig. 3.28.
Dans la réalité, l'air dans le thermique (et dans l'environnement mais
dans une moindre mesure) est également turbulent à plus petite échelle.
Cependant, comme on l'a dit plus haut,
les fluctuations de température associées avec ces fluctuations
de petite échelle de ![]() sont petites parce que
sont petites parce que ![]() est relativement
homogène verticalement, à la fois dans le thermique et dans l'environnement.
Avec une vue lagrangienne des choses, on peut dire qu'une fluctuation
positive de la température est attribuée à une particule de fluide qui provient
de la couche de surface. Dans une limite non visqueuse, que la trajectoire
empruntée par la particule soit une ligne droite ou qu'elle s'apparente
davantage à une marche aléatoire importe peu.
La vue un peu moins simpliste du thermique dans laquelle on superpose
de la turbulence de petite échelle au structures organisées
est illustrée sur les graphes du milieu de la Fig. 3.28.
Puisque les fluctuations à haute fréquence de
est relativement
homogène verticalement, à la fois dans le thermique et dans l'environnement.
Avec une vue lagrangienne des choses, on peut dire qu'une fluctuation
positive de la température est attribuée à une particule de fluide qui provient
de la couche de surface. Dans une limite non visqueuse, que la trajectoire
empruntée par la particule soit une ligne droite ou qu'elle s'apparente
davantage à une marche aléatoire importe peu.
La vue un peu moins simpliste du thermique dans laquelle on superpose
de la turbulence de petite échelle au structures organisées
est illustrée sur les graphes du milieu de la Fig. 3.28.
Puisque les fluctuations à haute fréquence de ![]() sont
seulement partiellement associées à des fluctuations de
sont
seulement partiellement associées à des fluctuations de ![]() , les
deux visions conduisent à des flux de chaleur comparables.
C'est bien ce que suggèrent les analyses en composite de
Williams (1991) présentées plus haut,
dont deux exemples sont reproduits en bas de la
Fig. 3.28.
, les
deux visions conduisent à des flux de chaleur comparables.
C'est bien ce que suggèrent les analyses en composite de
Williams (1991) présentées plus haut,
dont deux exemples sont reproduits en bas de la
Fig. 3.28.
|
En revanche, dans le haut de la couche mélangée et
dans la zone d'entraînement, le modèle ne reproduit correctement
ni les moments d'ordre deux de la température ni ceux du vent.
En fait, les processus en jeu dans cette région sont beaucoup plus
compliqués.
Ils sont résumés ici dans l'épluchage du thermique.
La réduction de l'aire fractionnaire au-dessus du niveau d'inversion cache
en fait des particules qui, après overshoot, redescendent pour être mélangées
dans l'environnement plus bas que leur niveau d'excursion maximale.
Si on prenait en compte ces aller-retours de façon plus explicite,
on pourrait aboutir à des flux de chaleur identiques mais pour des valeurs
de
![]() très supérieures.
On peut penser de même que les ondes de gravité, excitées
en particulier par la percussion
des panaches thermiques dans la couche d'inversion,
contribuent peu au flux de chaleur malgré des fluctuations
importante de température (dues au
fort gradient vertical de température potentielle à cette endroit).
Le fait que, dans les simulations des grands tourbillons, on ait encore des fluctuations importantes
de la température pour
très supérieures.
On peut penser de même que les ondes de gravité, excitées
en particulier par la percussion
des panaches thermiques dans la couche d'inversion,
contribuent peu au flux de chaleur malgré des fluctuations
importante de température (dues au
fort gradient vertical de température potentielle à cette endroit).
Le fait que, dans les simulations des grands tourbillons, on ait encore des fluctuations importantes
de la température pour
![]() , à une altitude où
, à une altitude où
![]() , souligne
le fait que seulement une part des fluctuations turbulentes est
impliquée dans des processus d'échange.
, souligne
le fait que seulement une part des fluctuations turbulentes est
impliquée dans des processus d'échange.
A titre d'illustration, on compare sur la Fig. 3.29
le vent horizontal simulé avec
la paramétrisation nominale et avec celle incluant un terme de traînée
(on choisit ![]() ).
Dans la version standard, le vent est constant dans le thermique
au-dessus de la couche de surface. Quand on introduit la traînée,
le thermique s'incline et le vent converge vers la valeur dans l'environnement.
L'impact n'est pas vraiment positif. C'est le genre de raffinements
auxquels on pourrait penser si on avait accès à des diagnostics
plus détaillés des simulations des grands tourbillons. Il faut cependant se souvenir
que l'impact sur les flux de chaleur et de traceurs est faible.
).
Dans la version standard, le vent est constant dans le thermique
au-dessus de la couche de surface. Quand on introduit la traînée,
le thermique s'incline et le vent converge vers la valeur dans l'environnement.
L'impact n'est pas vraiment positif. C'est le genre de raffinements
auxquels on pourrait penser si on avait accès à des diagnostics
plus détaillés des simulations des grands tourbillons. Il faut cependant se souvenir
que l'impact sur les flux de chaleur et de traceurs est faible.
|
On illustre l'impact de la nouvelle paramétrisation dans une configuration moins académique en utilisant le modèle de circulation générale en version unicolonne. Dans cette configuration, la couche limite est couplée aux autres processus comme le rayonnement et la résolution verticale est plus proche des configurations classiques des modèles de circulation. Pour ce faire, on s'appuie sur un cas de convection sèche bien développée, observé dans la région parisienne pendant la campagne ESQUIF, plus précisément lors de la seconde Période d'Observation Intensive de cette campagne (POI 2), en août 1998.
ESQUIF (``Étude et Simulation de la QUalité de l'air en Ile de France") est un projet dédié à l'étude et à la modélisation de la qualité de l'air dans la région parisienne (Menut, 2000). La POI 2 d'ESQUIF correspondait à une période très chaude, avec des vents faibles et sans nuages, c'est-à-dire un cas idéal pour tester le modèle du thermique. La POI 2 s'est déroulée du 7 au 11 août 1998, et précédait de peu un très important pic de pollution à l'ozone dans la région parisienne.
Pour la validation du modèle, on a utilisé les observations de la
température, de l'humidité relative et de la pression à 2 m au-dessus du
sol enregistrées toutes les heures par le réseau Mesonet de Météo-France
déployé autour de Paris. On a aussi utilisé les sondages de Trappes.
En plus des sondages effectués en routine à 00:00 et 12:00 (heures
TU comme toutes les heures utilisées dans cette section), nous disposions de
sondages additionnels effectués toutes les 3 heures.
La Fig. 3.30 illustre l'évolution de la structure de la couche limite
pendant la POI. La hauteur de la couche limite est marquée par des points
sur des profils de température potentielle. Cette hauteur est déterminée
à partir d'un seuil sur un nombre de Richardson non local,
![]() , calculé suivant l'Eq. 3.42.
Pour les sondages, on considère comme altitude de référence
, calculé suivant l'Eq. 3.42.
Pour les sondages, on considère comme altitude de référence ![]() le
premier point disponible sur les profils (situé entre 0 et 50 m suivant
les cas).
le
premier point disponible sur les profils (situé entre 0 et 50 m suivant
les cas).
|
Les 8 et 9 août correspondent à des conditions typiques de couche limite convective développée avec, la nuit, une couche limite écrasée dans les 300 premiers mètres et, l'après-midi, une température bien mélangée jusque 2300 m le 8 et 2800 m le 9 août.
Les simulations sont effectuées sur la période du 7 au 9 août en partant des sondages de 23:30, le 6. Le 7, qui ne présentait pas une couche convective bien développée, est utilisé comme période de mise en régime pour les paramétrisations. Les champs météorologiques sont à nouveau initialisés avec les sondages du 8 août à 5:30. Les résultats sont présentés pour les 8 et 9.
Dans les simulations, l'albédo de surface est fixé à 0,19 et la
longueur de rugosité à 0,4 m. L'inertie thermique de la surface est
ajustée à 3000 J m![]() s
s![]() K
K![]() , valeur typique des surfaces
continentales, de manière à reproduire correctement l'amplitude du
cycle diurne de la température de surface.
La température initiale du sol est fixée à 292 K dans les 11 niveaux du modèle
de sub-surface. Enfin, l'aridité du sol
, valeur typique des surfaces
continentales, de manière à reproduire correctement l'amplitude du
cycle diurne de la température de surface.
La température initiale du sol est fixée à 292 K dans les 11 niveaux du modèle
de sub-surface. Enfin, l'aridité du sol ![]() , qui relie l'évaporation
à l'humidité spécifique
, qui relie l'évaporation
à l'humidité spécifique ![]() selon
selon
![]() (Laval et al., 1981), ne varie pas au cours du temps
et est utilisée comme paramètre ajustable des simulations.
On prend finalement
(Laval et al., 1981), ne varie pas au cours du temps
et est utilisée comme paramètre ajustable des simulations.
On prend finalement ![]() pour obtenir une évolution de l'humidité
en surface comparable à celle observée sur les 3 jours.
pour obtenir une évolution de l'humidité
en surface comparable à celle observée sur les 3 jours.
|
Malgré des vents faibles, il faut prendre en compte le forçage grande échelle
dans ces simulations. Pour la vapeur d'eau, et parce que la POI était
dépourvue de nuages, l'humidité spécifique du modèle n'est affectée que par
l'évaporation en surface et la paramétrisation de la couche limite.
Dans l'atmosphère libre, on observe un assèchement systématique pendant
le 8 août qui ne peut s'expliquer que comme un effet de la grande échelle.
Il peut s'agir par exemple d'une advection d'air sec et chaud depuis le sud.
Afin de garder un forçage aussi simple que possible, on prescrit ce forçage
comme une subsidence
| (3.90) |
En principe, la dérivation est moins directe pour la température du fait de
l'importance du forçage radiatif. Cependant, comme le forçage radiatif
est sans doute assez bien simulé pendant cette période sans nuages, on
retient la même approche. Les résultats montrent qu'il faut rajouter un terme
de chauffage par la grande échelle pour obtenir un accord satisfaisant
dans la moyenne atmosphère. On retient la même forme que précédemment mais
avec ![]() Pa s
Pa s![]() pour le 8 août et
pour le 8 août et ![]() pour le 9.
pour le 9.
Dans les simulations que nous présentons ici, le vent horizontal est
directement forcé par des valeurs interpolées linéairement entre deux
radiosondages.
On utilise une discrétisation verticale
avec 40 couches, typique des résolutions qui seront utilisées avec le
modèle de circulation générale dans les années qui viennent.
Le premier niveau est centré
à environ 40 m au-dessus de la surface et le 15![]() niveau est
situé vers 4,4 km avec une résolution verticale de 500 m entre
1,5 et 3,5 km.
Le modèle est intégré avec un pas de temps de 3 minutes.
niveau est
situé vers 4,4 km avec une résolution verticale de 500 m entre
1,5 et 3,5 km.
Le modèle est intégré avec un pas de temps de 3 minutes.
nous présentons tout d'abord des comparaisons effectuées avec le modèle du thermique dans sa configuration nominale et les schéma de MY et HB. Sur la Fig. 3.31 on compare la température et l'humidité spécifique simulées dans le premier niveau du modèle avec les sondages de Trappes au même niveau et les mesures Mesonet à 2 m. A noter que le forçage du modèle a été réglé de façon à reproduire correctement la température de surface (dérive et amplitude du cycle diurne) et la dérive de l'humidité de surface observée à Trappes. Les mesures Mesonet, à 2 m au-dessus du sol, donnent une idée de la stabilité de la couche de surface et des fluctuations des champs météorologiques près de la surface.
La Fig. 3.32 montre une comparaison des sondages de Trappes avec les résultats
du modèle pour la température potentielle virtuelle ![]() (K)
et l'humidité spécifique
(K)
et l'humidité spécifique ![]() (g/kg) pour le 9 août à 5:30 et 17:30.
(g/kg) pour le 9 août à 5:30 et 17:30.
Pour les sondages de 5:30, les profils montrent deux couches d'inversion. La plus basse correspond au sommet de la couche limite nocturne avec un très fort gradient à 500 m au-dessus de la surface. La couche limite nocturne est bien représentée avec les 3 paramétrisations. Ceci n'est pas surprenant dans la mesure où on a modifié la paramétrisation de MY (aussi bien quand elle est utilisée seule qu'avec le modèle du thermique) pour les conditions très stables en suivant Holtslag et al. (1990) comme on l'explique plus haut. La couche résiduelle (vers 2200 m) est mieux simulée avec le modèle du thermique du fait d'une meilleure simulation de la couche convective le 8. Au-dessus de cette inversion résiduelle, les profils sont essentiellement déterminés par le forçage de grande échelle.
A 17:30 les profils sont le reflet des processus convectifs du début
d'après-midi. Le modèle du thermique montre un accord bien meilleur avec
les sondages, avec une hauteur de couche limite de 2500 m alors que
les schémas de HB et MY la trouvent vers 2000 m.
La surestimation de ![]() au-delà de 2700 m n'est due qu'au forçage de
grande échelle.
au-delà de 2700 m n'est due qu'au forçage de
grande échelle.
|
On effectue les mêmes tests de sensibilité que ceux présentés pour la comparaison aux simulations des grands tourbillons (Fig. 3.33). La sensibilité est généralement moindre. A noter en particulier que le détail de la façon dont on décrit le détraînement au-dessus de l'inversion importe peu, ce qui ce comprend aisément vue la résolution verticale très grossière à ce niveau.
|
On présente dans cette section des tests relatifs au transport des traceurs avec les nouveaux schémas de couche limite. On se concentre sur le mois d'août 1998, pour lequel on dispose à la fois des sondages de la POI2 d'ESQUIF et de mesures de Radon en continu en Europe, montrant un fort cycle diurne pour la même période. On utilise pour ce faire des simulations tridimensionnelles, zoomées sur le nord de la France et guidées par les réanalyses ERA40. Pour le vent, on utilise des constantes de temps de guidage différentes à l'extérieur (2h30) et à l'intérieur (1 jour) du domaine zoomé - en pratique cette constante est spécifiée comme une fonction de la taille de la maille considérée -. Pour la température et l'humidité relative, on applique une constante de temps uniforme de 1 jour. Le guidage est donc très peu contraignant pour le modèle à l'intérieur du maillage. Le guidage plus important du vent à l'extérieur du domaine garantit une bonne représentation de l'advection à grande échelle, en phase avec la situation synoptique observée. Sur la Fig. 3.34 on montre le maillage, la position du SIRTA et des deux stations de mesure du radon utilisées par la suite, l'une située à Heidelberg (HD), à basse altitude, et l'autre située au sommet du Jungfraujoch (JFJ), à 3400 m d'altitude.3.73.8
Comme pour les simulations unidimensionnelles présentées ci-dessus,
il est tout d'abord nécessaire d'ajuster l'inertie
thermique et l'humidité du sol.
Des tests discutés dans la conclusion de ce chapitre montrent que les modèles
de sol à notre disposition (y compris le modèle ORCHIDEE)
ne sont pas capables de maintenir
des concentrations d'eau correctes en l'absence de pluie.
On choisit donc d'imposer l'humidité du sol, ce qui revient à imposer
le facteur
.
On choisit pour le mois d'août ![]() , c'est-à-dire
10/75 où 10 mm est la hauteur d'eau dans le sol et 75 mm la hauteur
à partir de laquelle
, c'est-à-dire
10/75 où 10 mm est la hauteur d'eau dans le sol et 75 mm la hauteur
à partir de laquelle ![]() (se reporter à la description des
paramétrisations physiques de LMDZ, Section 2.1.3).
(se reporter à la description des
paramétrisations physiques de LMDZ, Section 2.1.3).
On montre sur la Fig. 3.35 les résultats d'une simulation de référence utilisant la version nominale du modèle du thermique (MY+TH). On voit que le modèle reproduit correctement à la fois l'évolution sur le mois et le cycle diurne de la concentration de radon mesurée à Heidelberg (HD) et des variables météorologiques en région parisienne. Pour les variables météorologiques, on compare sur cette figure les valeurs obtenues dans la première couche du modèle aux sorties des réanalyses ERA40 du ECMWF interpolées à la même altitude. Le réglage de l'inertie thermique (à 1700 USI) et de l'humidité du sol (à 10 mm d'eau) a été fait en privilégiant la première dizaine de jours. On voit qu'avec ce réglage, on sous-estime le cycle diurne après le 13 août, et ce à la fois pour la température et le radon.
|
|
|
|
On privilégie dans ce qui suit la période du 7 au 10 janvier qui correspondait à un fort cycle diurne estival, période au milieu de laquelle on bénéficie des radiosondages de la POI2 d'ESQUIF. La Fig. 3.36 montre pour cette période le cycle diurne moyen des différentes quantités montrées sur la Fig. 3.35 pour les simulations LMD(+CG), LMD+TH, MY et MY+TH. La température est bien réglée pour l'ensemble des simulations. Le cycle diurne du radon est relativement bien reproduit avec les différents modèles. Le radon, accumulé près de la surface la nuit dans la couche limite nocturne, se dilue au cours de la matinée en même temps que se développe la couche limite convective. On voit cependant que le cycle diurne des concentrations de surface est davantage sensible à la paramétrisation en diffusion qu'à l'utilisation ou non du modèle du thermique (qui tend à creuser un peu plus ce cycle diurne). A noter que des différences plus importantes étaient rapportées par Idelkadi (2002) mais qu'on s'est rendu compte par la suite que ces différences étaient dues en fait à des différences cachées dans la formulation de la diffusion turbulente.
Le cycle diurne observé se situe quelque part entre celui obtenu avec les schémas de MY et du LMD. Comme pour le radon, l'humidité est minimum près de la surface dans l'après-midi du fait du mélange vertical dans la couche limite convective. Cet effet domine largement celui du renforcement de l'évaporation dans la journée. L'apparent désaccord avec les données ERA40 semble en fait plutôt imputable aux réanalyses. En effet, la comparaison directe aux observations, pour les trois jours où nous disposons de radiosondages toutes les 3 heures (Fig. 3.37) est nettement plus favorable. Le cycle diurne est un peu trop faible pour le modèle LMD mais très bien représenté pour la simulation nominale MY+TH.
La Fig. 3.38 montre le cycle diurne moyen du radon et des variables météorologiques pour cette période et pour trois simulations avec différentes valeurs de l'humidité du sol. On voit que l'air est à la fois trop sec et trop chaud si on divise par deux la valeur du contenu en eau du sol. On obtient de façon symétrique un air trop humide et trop froid pour une humidité du sol deux fois plus grande. La version nominale est bien réglée à la fois en humidité et en température.
Si le cycle diurne des concentrations de surface est finalement relativement peu sensible à l'introduction du modèle du thermique, il n'en va pas de même en altitude. On montre sur la Fig. 3.39 les cycles diurnes moyens sur la verticale. On voit bien la montée plus rapide du radon sur les différences relatives, entre 9:00 et 15:00 UTC. En moyenne aussi, les simulations avec thermiques montrent des profils verticaux plus marqués avec moins de radon près de la surface et plus en sommet de couche limite (signature d'un épaississement de cette couche limite). Il est intéressant de noter que l'impact est relativement similaire pour les deux modèles de diffusion turbulente (LMD et MY).
|
Il existe malheureusement apparemment peu de données permettant de départager les modèles, même pour des différences aussi importantes. Les campagnes d'observation du radon en altitude sont relativement limitées et ont souvent été effectuées dans des conditions particulières, notamment dans des régimes de brises de mer sur les côtes. Les résultats de modélisation (des tests, non montrés, ont été effectués avec LMDZ pour certains de ces cas) montrent que les autres sources d'incertitudes sont souvent trop importantes pour apporter des réponses.
On montre cependant deux indications du meilleur comportement du modèle avec thermiques. C'est d'abord (Fig. 3.40) l'évolution de la concentration de radon pour le mois d'août à la station de Jungfraujoch. On peut penser que cette station, située sur un sommet relativement isolé, à 3400 m d'altitude, est souvent sensible au niveau moyen de radon à cette altitude plutôt qu'à des effets locaux. On compare sur la figure observations et résultats de simulations dans la couche du modèle correspondant à l'altitude de JFJ. On voit d'abord que le modèle reproduit raisonnablement l'évolution au cours du mois de l'ordre de grandeur des concentrations de radon. Les simulations sont très proches les unes des autres. On observe cependant des différences pour les 8, 9 et 14 août (et dans une moindre mesure le 7). Pour ces trois jours, les modèles avec thermiques (LMD+TH et MY+TH) prédisent des niveaux de radon plus élevées, en meilleur accord avec les observations. Il faut cependant prendre ces résultats plus comme une indication que comme une validation (faible nombre de jours concernés, non prise en compte des montagnes dans la prévision du transport vertical).
La Fig. 3.41 montre également les profils de vapeur d'eau à Trappes pour les 8 et 9 août. On retrouve des résultats similaires à ceux des simulations unidimensionnelles. L'introduction du modèle du thermique permet de prédire des couches limites plus étendues, en meilleur accord avec les sondages observés. On retrouve aussi le fait que l'effet des thermiques est relativement similaire pour les paramétrisations MY et LMD. La paramétrisation MY+TH se comporte globalement très bien.
Il est à noter que les résultats sont obtenus ici avec le modèle tridimensionnel guidé. Dans les simulations unidimensionnelles montrées précédemment, il avait fallu une phase d'ajustement pour prédire les forçages à grande échelle du modèle, essentiels pour obtenir un bon accord sur les profils verticaux simulés. Ici, les simulations sont évidemment beaucoup plus lourdes d'un point de vue informatique, mais le forçage grande échelle est calculé automatiquement par le modèle zoomé et guidé. Cette approche permet donc facilement d'effectuer des simulations contraintes sur de longues périodes de temps.
|
|
Pour finir, notons que si le cycle diurne des concentrations en surface semble relativement peu sensible à la paramétrisation des thermique, ces mesures peuvent cependant permettre de relever quelques grosses déficiences des paramétrisations. On montre pour illustration sur la Fig. 3.42 l'impact sur le cycle diurne de l'introduction d'un seuil minimum sur la diffusivité verticale quand on utilise le modèle du LMD. L'introduction de ce seuil dégrade considérablement la simulation du cycle diurne du radon. Ce seuil est effectivement activé dans la configuration nominale du modèle de climat afin d'éviter que ne se crée un découplage irréaliste entre la première couche d'atmosphère et la surface, notamment l'hiver dans les hautes latitudes. L'introduction de ce seuil, grandement bénéfique pour le climat des hautes latitudes, dégrade considérablement la simulation du cycle diurne du radon.
On a donc introduit dans le modèle LMDZ une nouvelle paramétrisation qui concerne une échelle intermédiaire entre les échelles ``diffuses" de la couche limite et les échelles de la convection nuageuse. Cette paramétrisation est inspirée des schémas en flux de masse de la convection nuageuse mais diffère fortement de ceux-ci par la fermeture employée, appuyée ici sur une analyse géométrique des structures méso-échelles organisées de la couche limite convective. Cette paramétrisation présente également de fortes analogies avec le schéma en convection asymétriques de Pleim et Chang (1992). Le flux dans l'ascendance est cependant spécifié très différemment. Dans le modèle de Pleim et Chang (1992), ce flux est inspirée des approches en similitude avec un profil de vitesse calculé à partir de la hauteur de la couche limite et des flux en surface. Ce modèle suppose également que l'ascendance est alimentée uniquement par la première couche du modèle. Comme le modèle en convection asymétrique, le modèle du thermique permet de rendre compte de façon relativement physique du transport de chaleur en remontant le gradient dans les couches limites convectives.
Avec la nouvelle paramétrisation, on arrive à reproduire assez fidèlement les résultats des simulations des grands tourbillons pour des cas de couche limite convective claire. Chose importante, le modèle permet de bien rendre compte de la sensibilité du transport à l'intensité relative des forçages thermique et mécanique de la turbulence.
Le modèle du thermique permet de prédire un certain nombre de variables comme la largeur des thermiques, les fluctuations turbulentes du vent ou de la température dans la couche mélangée. Les thermiques négligent complètement la composante de turbulence de petite échelle dans la couche limite. Cette hypothèse pourrait être levée en utilisant le modèle du thermique pour advecter l'énergie cinétique turbulente depuis la couche de surface, en prenant éventuellement en compte la génération de turbulence par cisaillement sur le bord du panache ascendant. Un tel raffinement ne sera envisagé que si il répond à des problèmes particuliers.
Certaines améliorations ont été entreprises ou sont envisagées sur le
modèle.
Le modèle d'origine commençait par calculer les caractéristiques
d'un thermique pour chaque
couche instable pour ensuite les regrouper en un thermique unique.
En fait, on peut en ne changeant que peu les résultats ne calculer
qu'un thermique depuis le début, en se donnant a priori le profil vertical
de l'entrainement vers le thermique (ce profil peut par exemple être
pris comme fonction de ![]() et de
et de
![]() ).
On allège ainsi les calculs de façon significative.
Les résultats de la Section 3.7 ont d'ailleurs été obtenus avec
cette version modifiée du schéma (le travail de modification a été effectué
par Catherine Rio).
).
On allège ainsi les calculs de façon significative.
Les résultats de la Section 3.7 ont d'ailleurs été obtenus avec
cette version modifiée du schéma (le travail de modification a été effectué
par Catherine Rio).
On pourrait également penser à rajouter un excès de température dans cette couche d'alimentation, tenant compte de la dispersion des températures prédite par exemple par la fermeture en diffusion. Le calcul de cet excès de température pourrait aussi inclure des aspects liés aux hétérogénéités de surface (albédo, îlots de chaleur). On pourrait également entraîner de l'air par mélange turbulent dans la couche mélangée, ce qui aurait tendance à faire décroître la flottabilité du thermique. Les comparaisons favorables avec les simulations des grands tourbillons suggèrent soit qu'une tel calcul ne serait pas opportun soit que les résultats seraient peu sensibles à une telle sophistication.
Les résultats sont finalement assez frustrants en ce qui concerne le transport des traceurs. Les simulations donnent des résultats relativement différents, mais le nombre de degrés de liberté et le faible nombre de données (en particulier en altitude) sont tels qu'ils ne suffisent pas à départager les résultats. La vapeur d'eau, malgré sa source plus complexe, est peut-être finalement un meilleur traceur que le radon du fait du grand nombre de données disponibles. A noter également l'importance de la validation simultanée de la météorologie en surface quand on s'intéresse au transport vertical dans la couche limite. Dans l'avenir, la combinaison des profils aérosols du SIRTA et des mesures de vapeur d'eau et éventuellement de CO obtenus au décollage et à l'atterrissage par un certain nombre d'avions de lignes dans le cadre du programme MOZAIC, pourrait permettre d'avancer sur ce point.
On peut également penser dans l'avenir à utiliser de façon beaucoup plus systématique les traceurs pour valider le comportement des paramétrisations par rapport aux simulations des grands tourbillons. Un tel travail est actuellement entrepris en collaboration entre le LMD et le CNRM. Les collaborateurs du CNRM devraient en particulier refaire tourner les cas de Ayotte et al. (1996) avec des traceurs émis dans chaque couche (quelque chose d'analogue au travail de Ebert et al., 1989, sur les matrices de transiliences). C'est aussi une approche qu'on compte promouvoir dans le cadre du projet AMMA d'étude de la mousson africaine.
Pour les simulations des grands tourbillons, il serait également particulièrement intéressant d'effectuer des analyses en composites d'évènements chauds similaires à celles réalisées par Williams et Hacker (1992) pour les observations avions.
L'étape suivante du travail sur la paramétrisation concerne les nuages. Les rétroactions nuageuses sont à l'heure actuelle une des plus grandes sources d'incertitude des modèles de climat. On sait aussi que ces modèles de climat soufrent encore souvent de gros défauts concernant la représentation des nuages.
Il est couramment admis par exemple que les modèles de climat on tendance à sous-estimer la couverture nuageuse basse et moyenne (même si les jeux de données sont souvent insuffisant pour quantifier une telle allégation). Une intercomparaison récente de modèles basée sur l'utilisation du simulateur de radiances ISCCP3.9, à la quelle le modèle LMDZ4 a participé (Zhang et al., 2004), confirme en tous cas la grande dispersion des modèles.
Le modèle du thermique est a priori particulièrement adapté à la
simulation des cumulus de couche limite.
Un travail dans cette direction a déjà commencé.
On a notamment essayé de simuler les cas de cumulus montrés sur la
Fig. 3.7.
Plusieurs sophistications du modèle peuvent être envisagées pour ce faire.
D'abord, on peut, comme pour la convection profonde, coupler le
schéma de nuages au modèle du thermique.
Comme on l'a rapidement expliqué dans la présentation de la partie
physique de LMDZ, la fraction nuageuse, ![]() , et le contenu en eau condensé,
, et le contenu en eau condensé,
![]() ,
du nuage étaient précédemment prédits dans le modèle à
partir de l'eau totale dans la maille, , et de l'eau à saturation,
(calculée à partir de la température à grande échelle), en utilisant
une distribution de probabilité de forme imposée
,
du nuage étaient précédemment prédits dans le modèle à
partir de l'eau totale dans la maille, , et de l'eau à saturation,
(calculée à partir de la température à grande échelle), en utilisant
une distribution de probabilité de forme imposée
![]() pour la distribution sous-maille de l'eau totale.
Avec ces notations, la fraction nuageuse (fraction de la maille où l'eau
totale dépasse la saturation) est donnée par
pour la distribution sous-maille de l'eau totale.
Avec ces notations, la fraction nuageuse (fraction de la maille où l'eau
totale dépasse la saturation) est donnée par
| (3.91) |
Au cours du réglage du modèle de climat, et après l'introduction du
modèle d'Emanuel pour la convection profonde, on a modifié ce schéma
en suivant le travail de Bony et Emanuel (2001). D'une part, on remplace les
distributions carrées par des fonctions log-normales généralisées bornées
en zéro. Ainsi bornées, ces fonctions présentent une asymétrie vers les
valeurs positives, et cette asymétrie est d'autant plus grande
que le rapport
![]() (où
(où ![]() est comme précédemment la
largeur de la distribution) est grand.
Des grandes valeurs de
est comme précédemment la
largeur de la distribution) est grand.
Des grandes valeurs de ![]() correspondent donc à la fois à une grande
dispersion des humidités et à une forte asymétrie positive. C'est typiquement
ce qui est observé dans les cumulus qui présentent des humidités
très fortes mais sur une étendue relativement faible, au milieu
d'un environnement très sec.
Le deuxième grand changement consiste à ne plus imposer la largeur de la
distribution mais à la calculer en partant de l'eau nuageuse prédite
par la paramétrisation de la convection.
Ici, typiquement, on prendra pour
correspondent donc à la fois à une grande
dispersion des humidités et à une forte asymétrie positive. C'est typiquement
ce qui est observé dans les cumulus qui présentent des humidités
très fortes mais sur une étendue relativement faible, au milieu
d'un environnement très sec.
Le deuxième grand changement consiste à ne plus imposer la largeur de la
distribution mais à la calculer en partant de l'eau nuageuse prédite
par la paramétrisation de la convection.
Ici, typiquement, on prendra pour ![]() la valeur de
la valeur de
![]() ou
ou ![]() est l'eau totale dans le thermique et on en déduira
le paramètre de largeur de la distribution nuageuse en inversant
l'Eq. 3.93.
L'introduction de ce couplage pour le schéma de convection d'Emanuel
a joué un rôle déterminant dans l'amélioration
de la représentation des forçages radiatifs dans le modèle LMDZ.
Les premiers tests de couplage avec le modèle du thermique sont
également encourageants.
est l'eau totale dans le thermique et on en déduira
le paramètre de largeur de la distribution nuageuse en inversant
l'Eq. 3.93.
L'introduction de ce couplage pour le schéma de convection d'Emanuel
a joué un rôle déterminant dans l'amélioration
de la représentation des forçages radiatifs dans le modèle LMDZ.
Les premiers tests de couplage avec le modèle du thermique sont
également encourageants.
La deuxième modification possible en présence de nuages concerne la fermeture. L'idée la plus simple serait de remplacer la CAPE sèche par une CAPE humide (on tient compte du dégagement de chaleur latente dans le calcul de la flottabilité). Mais se pose alors immédiatement la question de la transition vers la convection profonde et de l'articulation avec les paramétrisations utilisées pour cette convection. En effet, la fermeture du modèle du thermique est basée sur une image de la couche limite convective très éloignée des images de la convection profonde où les processus de condensation, les descentes précipitantes ou les fronts de rafales créés devant les proches froides jouent un rôle déterminant. Des tests on commencé dans le modèle de circulation pour regarder l'articulation entre le modèle du thermique et la paramétrisation de la convection profonde. On revient sur ces aspects dans la conclusion générale du document.
Pour clore ce chapitre, soulignons le potentiel qu'offre pour le travail sur les paramétrisations la version guidée et zoomée du modèle. Pour illustrer davantage ce point, on montre des simulations réalisées par Coindreau et al. (2006) avec la configuration de grille présentée plus haut et avec différentes versions du modèle. Ces simulations étaient réalisées pour valider et ajuster une version régionale de LMDZ adaptée à l'étude des paramétrisations au SIRTA et à la surveillance de l'environnement.
Les simulations sont effectuées sur une période de 6 ans entre 1998 et 2004. Pour le vent, l'humidité relative et la température, les constantes de temps de rappel sont fixées à 30 minutes à l'extérieur du domaine zoomé et 10 jours à l'intérieur afin de laisser le maximum de degrés de liberté au modèle dans la région d'intérêt et éviter les dérives à l'extérieur.3.10On montre tout d'abord sur la Fig. 3.43 l'évolution simulée de la température à 2 m à Trappes pour les années 2000 à 2004. On voit que le modèle surestime de façon significative le cycle saisonnier, avec des températures trop chaudes de 5 degrés environ l'été. Chose intéressante à noter, ce biais est tout à fait similaire à celui observé dans le modèle climatique standard qui surestime largement les températures estivales sur les continents de l'hémisphère nord. On retrouve ce biais chaud estival pour toutes les simulations montrées ici, en utilisant la couche limite originale du LMD (LMD) ou le modèle du thermique couplé à MY (MY+TH), en utilisant le schéma de Tiedtke (TI) ou d'Emanuel (KE) pour la convection profonde, ou encore en utilisant le modèle de sol en saut d'eau (BUCKET) ou le modèle ORCHIDEE. On voit cependant que l'utilisation du modèle BUCKET aboutit à un cycle saisonnier moins en phase.
|
|
Ce comportement est bien visible si on regarde le cycle saisonnier moyen de la température (en haut à gauche de la Fig. 3.44). Ce comportement est fortement corrélé à celui de l'humidité relative. On voit en effet que la surestimation des températures estivales est associée à une trop grande sécheresse. Le comportement spécifique du modèle en saut d'eau s'explique aussi à partir de l'humidité. En hiver et au début du printemps, quand le bilan précipitation moins évaporation est positif, le sol est gorgé d'eau et le modèle surestime l'évaporation (égale à l'évaporation potentielle dans ces conditions). Les températures sont donc trop froides. Quand le bilan devient négatif, le sol se vide rapidement et on retrouve finalement en août un air aussi sec et aussi chaud que dans les simulations avec ORCHIDEE. On voit en fait que le contenu en eau du sol est au plus de l'ordre de quelques millimètres l'été (en bas à droite de la figure) alors qu'on a vu dans les tests plus haut qu'il fallait conserver des humidités de l'ordre de 10 mm en août avec la formule utilisée dans le modèle BUCKET.
Le phasage saisonnier est meilleur quand on utilise ORCHIDEE. Cependant, le modèle n'arrive pas à suffisamment évaporer l'été, malgré un contenu en eau qui est loin de s'annuler. Le modèle ORCHIDEE contient en fait deux réservoirs d'eau. Un réservoir superficiel et un réservoir profond. C'est le contenu de ce dernier qui est montré sur la figure. Il semble que la capacité à évaporer l'eau stockée dans ce réservoir profond soit très insuffisante dans le modèle.
On voit que le modèle a suffisamment de liberté pour véritablement évaluer les paramétrisations du modèle de climat. A noter que des rétroactions complexes du modèle complet de climat sont ici mises en jeu. Par exemple, la surestimation de l'humidité en hiver avec le BUCKET aboutit à des pluies plus importantes qui renforcent en retour l'humidité du sol. On voit aussi que le modèle, même biaisé, permet de retrouver des éléments de la variabilité inter-annuelle comme la canicule de 2003. On peut donc envisager de décortiquer certains des mécanismes mis en jeu avec cet outil.
En attendant de disposer d'un modèle de surface plus performant (le modèle à dix couches développé par Patricia De Rosnay devrait être testé prochainement), on compte imposer un cycle saisonnier de l'humidité du sol pour éviter les gros biais saisonniers montrés ici. Cette étape est essentielle si l'on veut travailler plus finement sur la dynamique de la couche limite et des nuages associés, en tirant avantage de l'instrumentation sophistiquée installée au SIRTA (mesures météo classiques, mat, radiomètres, lidars, radars).
Le troisième volet de ce travail concerne l'inversion du transport atmosphérique. Il a été initié suite à une demande du CEA visant à évaluer l'efficacité du réseau global de mesure de la radioactivité atmosphérique déployé dans le cadre du Traité d'Interdiction Complète des Essais nucléaires (TICE). La surveillance des essais reposera sur quatre réseaux complémentaires. Les trois premiers mesureront les ondes sismiques, hydroacoustiques et infra-sonores et devraient permettre de localiser relativement bien les explosions pour des essais effectués respectivement sous terre, dans la mer ou dans l'atmosphère. En parallèle de ces trois technologies, un réseau global de 80 stations, en cours de déploiement, mesurera en permanence la concentration en radio-éléments dans l'atmosphère permettant de mieux caractériser le type d'évènement détecté. Toutes ces stations détecterons les aérosols radioactifs. Un sous-réseau de 40 stations détectera également les isotopes du xénon dont on pense qu'il sont relâchés en quantité significative dans l'atmosphère même lors d'essais souterrains ou sous-marins.
La question qui nous était posée par le CEA était l'évaluation de la capacité de détection de ce réseau. A l'époque (été 1997), nous disposions d'une première version de LMDZT qui permettait d'effectuer des calcul de dispersion de polluants ou de radio-éléments atmosphériques. Pour répondre à la question, une approche directe aurait consisté à simuler des essais nucléaires en injectant un traceur en chaque point d'un maillage de la sphère (en chaque point de grille du modèle de transport par exemple) et de comptabiliser les fois où la concentration simulée aux différentes stations du réseau excédait le seuil de détection. On voit vite qu'une telle approche conduit à des coûts informatiques prohibitifs. Avec Robert Sadourny (LMD), nous nous sommes convaincus que ce problème pouvait être abordé en inversant le sens du temps dans notre modèle de transport Eulérien, le calcul du transport étant effectué alors en remontant à rebours dans le temps le long des trajectoires atmosphériques.
L'idée d'utiliser des modèles de récepteurs pour ce type
de problème n'est pas nouvelle.
De façon générale, l'identification des sources pour un traceur atmosphérique
(localisation spatiale et temporelle des sources ainsi que la quantification
de la quantité de traceur émise) est une question très importante pour
beaucoup d'aspects des sciences de l'environnement.
La caractérisation des puits et sources naturels et anthropiques
de CO![]() (Gurney et al., 2002; Rayner et al., 1999; Kaminski et al., 1999b; Bousquet et Peylin, 2000)
est par exemple un sujet très sensible dans la perspective du contrôle
des émissions de gaz à effet de serre.
La surveillance de possibles rejets accidentels de pollution par des
centrales nucléaires ou des installations chimiques est un autre bon
exemple. Les inventaires d'émissions d'espèces chimiques qui alimentent
les modèles de prévision de la pollution atmosphérique doivent aussi souvent
être en partie construits en utilisant des méthodes inverses, à partir de la
comparaison des prévisions du modèle et des observations
(voir e. g. Menut, 2000).
Autre exemple encore, l'interprétation fine en termes de paléoclimats
des carottages effectués sur les calottes de glace en Antarctique ou au
Groënland, nécessite qu'on soit capable de remonter à l'origine de l'eau
qui a précipité sur les calottes ou des molécules gazeuses et aérosols
qui s'y sont sont accumulés.
(Gurney et al., 2002; Rayner et al., 1999; Kaminski et al., 1999b; Bousquet et Peylin, 2000)
est par exemple un sujet très sensible dans la perspective du contrôle
des émissions de gaz à effet de serre.
La surveillance de possibles rejets accidentels de pollution par des
centrales nucléaires ou des installations chimiques est un autre bon
exemple. Les inventaires d'émissions d'espèces chimiques qui alimentent
les modèles de prévision de la pollution atmosphérique doivent aussi souvent
être en partie construits en utilisant des méthodes inverses, à partir de la
comparaison des prévisions du modèle et des observations
(voir e. g. Menut, 2000).
Autre exemple encore, l'interprétation fine en termes de paléoclimats
des carottages effectués sur les calottes de glace en Antarctique ou au
Groënland, nécessite qu'on soit capable de remonter à l'origine de l'eau
qui a précipité sur les calottes ou des molécules gazeuses et aérosols
qui s'y sont sont accumulés.
Nous nous intéressons donc dans ce chapitre à l'inversion du transport atmosphérique, c'est à dire aux approches permettant de remonter à l'identification des sources à partir de mesures de concentration dans l'atmosphère. A noter que l'inversion du transport, au-delà des nombreuses applications mentionnées ci-dessus, est un outil très intéressant pour analyser la dynamique et la chimie de l'atmosphère.
Une première approche, fréquemment utilisée pour interpréter des mesures de concentration dans l'atmosphère, consiste à remonter à rebours dans le temps le long des trajectoires des masses d'air. On parle alors de rétro-transport Lagrangien ou de rétro-trajectoires. Cette technique permet d'obtenir facilement une description qualitative de l'origine de la masse d'air échantillonnée lors d'une mesure de concentration (Chiapello et al., 1997; Ramonet et al., 1996; Hess et al., 1996; Merrill, 1994; Veron et al., 2000). Comme dans les modèles lagrangiens directs, la composante turbulente du transport peut être prise en compte au moyen de perturbations aléatoires des trajectoires (Vautard et al., 2001; Siebert et Frank, 2003; Flesch et al., 1995). Cependant, les calculs de rétro-trajectoires sont souvent limités à la composante grande échelle.
Curieusement, alors que de nombreux modèles directs sont basés sur une description eulérienne du transport, le rétro-transport est généralement réservé à une description lagrangienne. On montre ici qu'on peut de façon générale, comme dans le monde direct, définir le rétro-transport le long des trajectoires d'air parcourues à rebours dans le temps, et lui appliquer les outils et approches utilisées habituellement pour le transport direct : formalismes Lagrangien ou Eulérien, décomposition de Reynolds entre transport grande échelle et turbulent, schémas numériques sophistiqués pour l'advection (monotones, conservatifs, peu diffusifs, etc.). L'équation du rétro-transport se déduit de l'équation directe par des transformations simples. La diffusion turbulente, basée sur l'idée de mélange par des fluctuations symétriques du champs de vent, produit par exemple la même diffusion pour le transport direct et à rebours. Pour les paramétrisations en flux de masse de la convection, il faut en revanche inverser la direction des flux de masse dans les différents compartiments. C'est sur ces idées physiques que nous avons développé une version rétro-transport du modèle de transport LMDZT (Hourdin et al., 1999) dans sa version débranchée (il s'agit d'inverser le transport de traceurs à météo connue).
Le rétro-transport, ainsi défini,
peut être utilisé pour des inversions quantitatives
en tirant avantage d'une symétrie temporelle du transport.
En absence d'autres sources ou puits, la concentration
d'un traceur mesurée par un détecteur à un instant ![]() , faisant
suite à l'injection d'une certaine quantité de traceur à un point
source à un instant antérieur
, faisant
suite à l'injection d'une certaine quantité de traceur à un point
source à un instant antérieur ![]() , peut être calculée également comme
la concentration au niveau de la source à l'instant
, peut être calculée également comme
la concentration au niveau de la source à l'instant ![]() d'un rétro-traceur émis en même quantité au lieu de détection à l'instant
d'un rétro-traceur émis en même quantité au lieu de détection à l'instant
![]() .
Ce rétro-traceur correspond (à un facteur multiplicatif près) à la distribution
de l'air qui va être échantillonné ultérieurement au niveau du détecteur.
A noter qu'on ne viole pas ici l'irréversibilité du transport atmosphérique.
Une plus forte dispersion ou diffusion dans le monde direct, correspondant
à un gain d'entropie, se traduit également par une origine de l'air
échantillonnée plus diffuse et donc également par un gain d'entropie pour
le rétro-transport.
Le gain d'entropie ou la perte d'information est en fait identique dans les
deux cas.
.
Ce rétro-traceur correspond (à un facteur multiplicatif près) à la distribution
de l'air qui va être échantillonné ultérieurement au niveau du détecteur.
A noter qu'on ne viole pas ici l'irréversibilité du transport atmosphérique.
Une plus forte dispersion ou diffusion dans le monde direct, correspondant
à un gain d'entropie, se traduit également par une origine de l'air
échantillonnée plus diffuse et donc également par un gain d'entropie pour
le rétro-transport.
Le gain d'entropie ou la perte d'information est en fait identique dans les
deux cas.
Une seconde approche utilisée classiquement pour l'inversion du transport atmosphérique consiste à partir d'un modèle existant du transport direct, aussi complexe soit-il, et à lui appliquer les techniques classiques de l'assimilation des observations telles que des variantes de l'interpolation optimale, ou l'assimilation variationnelle (voir par exemple Pétron, 2002), les filtres ou lissages de Kalman (Zhang et al., 1999; Haas-Laursen et al., 1996). En particulier, les techniques adjointes, qui remontent aux travaux de Lions et Marchuk (se reporter par exemple à Lions, 1971; Marchuk, 1982,1974), fournissent une méthode systématique et puissante pour déterminer les sensibilités d'un modèle par rapport à ses variables d'état ou à des paramètres de contrôle. Ces méthodes sont généralement introduite sur des bases purement mathématiques sans référence à une quelconque signification physique.
Les techniques adjointes sont utilisées pour de nombreuses applications tant météorologiques qu'océanographiques, en particulier pour l'assimilation variationnelle d'observations (Penenko et Obraztsov, 1976; Courtier et Talagrand, 1987; Le Dimet et Talagrand, 1986; Talagrand et Courtier, 1987). Les techniques adjointes ont également été utilisées dans de nombreuses études relatives à l'inversion du transport atmosphérique (Pudykiewicz, 1998; Uliasz et Pielke, 1991; Vukicevic et Hess, 2000; Robertson et Persson, 1991; Houweling et al., 1999; Kaminski et al., 1999a,b). Si l'observable considérée est une mesure de concentration à un instant donné et à une station particulière, l'équation de transport adjointe est en fait un modèle "orienté récepteur" de la mesure, restreint aux processus qui vont effectivement influencer cette observation particulière. Le calcul adjoint détermine la sensibilité ou encore la fonction d'influence, qui, une fois combinée avec les sources et la concentration initiale du traceur, permet de calculer effectivement l'équivalent de la mesure.
A partir de la propriété de symétrie du transport,
on montre facilement que l'équation
de rétro-transport, définie plus haut sur des considérations physiques,
est en fait l'adjoint de l'équation du transport direct pour un
produit scalaire particulier, le produit scalaire pondéré par
l'air
Si on utilise un produit scalaire plus classique de la forme
![]() , la symétrie est mise à mal et les équations
directes et adjointes prennent des formes différentes
(cf. e. g. Pudykiewicz, 1998; Vukicevic et Hess, 2000).
Uliasz et Pielke (1991) étaient en fait déjà arrivés sur un jeu d'équations symétriques
en utilisant pourtant un produit scalaire non pondéré, mais ils utilisaient
une approximation de Boussinesq pour le fluide, ce qui rend en fait
les deux produits scalaires équivalents. Uliasz et Pielke (1991) avaient également
déjà remarqué l'essentiel à savoir
que ``la fonction d'influence peut se calculer à partir
de rétro-trajectoires particulaires quand on utilise un modèle Lagrangien.
Les modèles Eulériens, gouvernés par des équations aux dérivées partielles,
sont formulés dans un cadre variationnel et, dans ce cas,
la fonction d'influence peut
s'obtenir comme solution de l'équation adjointe à rebours dans le temps,
en utilisant le récepteur comme source."
Aux vues des considérations ci-dessus, on est tenté de récrire ce paragraphe
sous une forme un peu plus symétrique : la fonction d'influence peut
être obtenue soit en suivant à rebours dans le temps la masse d'air
échantillonnée au niveau du détecteur (rétro-transport) soit comme solution
de l'équation adjointe, et ce indépendamment du cadre (Eulérien ou Lagrangien)
choisi pour représenter le transport atmosphérique.
, la symétrie est mise à mal et les équations
directes et adjointes prennent des formes différentes
(cf. e. g. Pudykiewicz, 1998; Vukicevic et Hess, 2000).
Uliasz et Pielke (1991) étaient en fait déjà arrivés sur un jeu d'équations symétriques
en utilisant pourtant un produit scalaire non pondéré, mais ils utilisaient
une approximation de Boussinesq pour le fluide, ce qui rend en fait
les deux produits scalaires équivalents. Uliasz et Pielke (1991) avaient également
déjà remarqué l'essentiel à savoir
que ``la fonction d'influence peut se calculer à partir
de rétro-trajectoires particulaires quand on utilise un modèle Lagrangien.
Les modèles Eulériens, gouvernés par des équations aux dérivées partielles,
sont formulés dans un cadre variationnel et, dans ce cas,
la fonction d'influence peut
s'obtenir comme solution de l'équation adjointe à rebours dans le temps,
en utilisant le récepteur comme source."
Aux vues des considérations ci-dessus, on est tenté de récrire ce paragraphe
sous une forme un peu plus symétrique : la fonction d'influence peut
être obtenue soit en suivant à rebours dans le temps la masse d'air
échantillonnée au niveau du détecteur (rétro-transport) soit comme solution
de l'équation adjointe, et ce indépendamment du cadre (Eulérien ou Lagrangien)
choisi pour représenter le transport atmosphérique.
La symétrie du transport à la base de cette équivalence peut cependant être perdue dans le monde numérique, c'est à dire que le modèle numérique intégré à rebours dans le temps peut être différent de l'adjoint du code numérique direct. En particulier, seuls les opérateurs linéaires par rapport à la concentration du traceur ont un adjoint et peuvent donc respecter la symétrie temporelle. Les schémas sophistiqués utilisés aujourd'hui pour l'advection des traceurs dans la plupart des modèles introduisent des non linéarités pour garantir un meilleur comportement physique (conservation, positivité, monotonie, faible diffusion). Ces schémas ne sont donc pas symétriques. C'est le cas en particulier du schéma de Van Leer utilisé dans LMDZ. On montre en revanche que les codes numériques utilisés dans LMDZ pour calculer le transport turbulent ou convectif respectent bien l'équivalence entre transport rétro et adjoint.
Dans le cas où cette symétrie n'est pas respectée, la question se pose de savoir s'il est préférable d'utiliser le code adjoint du code direct ou d'intégrer à rebours dans le temps le modèle direct. Dans le cas des schémas d'advection, l'utilisation du rétro-transport garantira la positivité des rétro-panaches alors que le calcul adjoint pourra faire apparaître des valeurs négatives non physiques (une mesure de concentration pouvant augmenter à la suite d'une émission moindre). Dans certains algorithmes d'inversion, la positivité de la source peut être une contrainte importante, auquel cas on aura tendance à privilégier le rétro-transport. Pour des algorithmes de minimisation linéaires, utilisant des descentes de gradient, on peut penser a contrario que le code adjoint, qui fournit un calcul exact du gradient, doit être privilégié. On montre ici, sur des cas académiques, que cette conclusion est un peu trop rapide et que, même dans ce cas, l'utilisation d'un gradient approché mais garantissant certaines propriétés physiques peut permettre une minimisation moins poussée mathématiquement mais plus robuste.
Dans ce chapitre, nous revenons en détail sur l'ensemble des aspects introduits ci-dessus. Nous commençons par introduire (Section 4.2) le rétro-transport et la symétrie du transport atmosphérique pour des sources et détecteurs ponctuels et montrons comment le rétro-transport ainsi défini s'étend aux processus diffusifs. Nous expliquons dans la même section le lien avec l'équation adjointe et étendons la théorie à des sources diffuses. Nous explicitons en particulier ce lien entre rétro-transport et équations adjointes sur le cas des schémas de convection en flux de masse (Section 4.3). La discussion, développée d'abord dans le monde analytique, est ensuite étendue au monde numérique en présentant tout d'abord une illustration numérique du rétro-transport dans le cas de la campagne ETEX (Section 4.4). On démontre la symétrie des algorithmes utilisés dans LMDZ pour le transport turbulent et convectif. On étudie ensuite le cas des schémas non symétriques en se focalisant sur le schéma de Van Leer utilisé dans LMDZ (Section 4.5). Le chapitre se termine par quelques illustrations relatives à des applications menées autour de l'utilisation inverse du modèle LMDZ, et notamment des résultats relatifs à la surveillance des essais nucléaires.
Ce travail doit beaucoup aux discussions initiales avec Robert Sadourny. La sollicitation et le financement des études par Jean-Pierre Issartel puis Philippe Heinrich (CEA/DAM) ont permis de mener le travail au-delà du simple cadre académique. Ce travail a aussi bénéficié de nombreuses et fructueuses discussions avec Bertrand Cabrit. Les tests et illustrations ETEX ont été réalisés par Abderrahmane Idelkadi pendant sa thèse. Le travail sur le TICE a vu passer plusieurs stagiaires comme Alexandre Maes et Elie Anselin. Enfin Olivier Talagrand a été d'une aide précieuse pour mener à bien la mise en forme de la partie adjointe et l'écriture d'un article en deux parties sur le lien entre transport rétro et adjoint (Hourdin et Talagrand, 2005; Hourdin et al., 2005), article sur lequel repose largement le présent chapitre.
Cette question du rétro-transport nous a donc été posée dans un cadre militaire. Il s'agissait d'évaluer la capacité d'un réseau de stations mesurant la radioactivité atmosphérique à détecter et si possible localiser des essais nucléaires.
Nous avions donc une source, relativement ponctuelle en espace et en temps, et des détecteurs. La capacité de détection peut être évaluée avec une méthode directe de la façon suivante : en un point de la planète, on injecte la quantité de radio-élément correspondant à un essai nucléaire typique (l'objectif retenu par le TICE était de détecter des essais de 1 kt équivalent TNT au plus 15 jours après le tir partout sur le globe). On transporte ce radio-élément sur quinze jours en regardant si à une des stations du réseau, la concentration en radio-élément dépasse le seuil de détection des stations de mesure au cours de cette période. Reste à effectuer ce calcul à partir de tous les points du globe (les points d'un maillage globale par exemple) et pour un ensemble statistiquement représentatif de situations météorologiques.
Il est beaucoup plus efficace de traiter ce problème en mode rétro-transport.
Dans ce cas particulier, la symétrie est complète comme on le montre
ci-dessous. On peut en fait injecter
la quantité de radio-élément à la station puis inverser le sens du temps dans
le modèle. Les points de la planètes auxquels un essai aurait été détecté
dans les 15 jours précédents sont ceux où la concentration du
rétro-radio-élément dépasse le seuil de détection.
Dans ce cas précis, le rapport de coût numérique entre le calcul direct
et rétro est le rapport entre
le nombre de stations et le nombre de localisations testées.
Pour un réseau d'une cinquantaine de stations et un maillage avec une
résolution de quelques centaines de kilomètres, disons 10![]() points,
le rapport est de l'ordre de 200.
points,
le rapport est de l'ordre de 200.
On commence ici par introduire la symétrie du transport atmosphérique dans le cas d'une source et d'un détecteur ponctuels (comme dans le cas des calculs effectués pour le TICE) à partir de considérations physiques. On montre ensuite comment on peut retrouver la même propriété de symétrie de façon mathématique à partir de l'approche adjointe.
On introduit tout d'abord la symétrie du transport atmosphérique
en s'intéressant à un traceur parfait (qui suit les trajectoires fluides
sans source ni puits) distribué uniformément à un instant ![]() dans un
volume source
dans un
volume source ![]() . On suppose que la détection consiste en
la mesure de la concentration moyenne de traceur dans un volume
. On suppose que la détection consiste en
la mesure de la concentration moyenne de traceur dans un volume ![]() au temps
au temps ![]() .
Pour une quantité totale injectée
.
Pour une quantité totale injectée ![]() (quantité extensive en kg, atomes, ...),
la concentration massique moyenne
(quantité extensive en kg, atomes, ...),
la concentration massique moyenne ![]() (pour mesure)
de traceur dans
(pour mesure)
de traceur dans ![]() à
à ![]() peut s'écrire
peut s'écrire
A : Le domaine B : Idéalisation de la dilution d'un polluant injecté le matin près de la surface, dans une couche limite nocturne peu épaisse (l'air pollué est montré en gris sombre), et mélangé en milieu de journée dans la couche limite convective pour donner en soirée un air moins pollué (gris clair). La concentration observée en soirée peut être obtenue soit en injectant le polluant le matin et en le mélangeant complètement sur la verticale à midi, soit par un calcul inverse, en injectant le polluant près de la surface le soir, et en le mesurant le matin précédent, en appliquant en milieu de journée le même mélange vertical que lors du calcul direct. |
On peut donner une illustration de cette réciprocité dans deux cas extrêmes.
La première illustration (partie A de la Fig. 4.1)
s'apparente à une vision de type advection
des contours. Pour simplifier l'image,
on va s'intéresser à un écoulement bidimensionnel non divergent.
Dans la limite d'un écoulement non visqueux, on sait que l'advection va
se contente de déformer (et déplacer) la surface ![]() contenant initialement
le traceur.
Supposons que la nouvelle surface obtenue au temps
contenant initialement
le traceur.
Supposons que la nouvelle surface obtenue au temps ![]() après advection
intersecte
après advection
intersecte ![]() .
Cette intersection contient tout l'air qui venait de
.
Cette intersection contient tout l'air qui venait de ![]() et qui se trouve
actuellement dans
et qui se trouve
actuellement dans ![]() . De façon symétrique, si on remonte depuis
. De façon symétrique, si on remonte depuis
![]() le long des trajectoires
fluides, les points de l'intersection doivent revenir dans
le long des trajectoires
fluides, les points de l'intersection doivent revenir dans ![]() alors que les
autres points du volume
alors que les
autres points du volume ![]() vont se disperser autour (par exemple sous
forme d'un filament).
vont se disperser autour (par exemple sous
forme d'un filament).
Le second cas est celui d'une couche limite nocturne, épaisse de 500 m
pour fixer les idées,
dans laquelle on injecte un polluant en surface. A midi, on suppose
qu'une couche limite convective se développe brassant complètement l'air
sur 2 km. Si on détecte la pollution en surface après le brassage, elle
sera 4 fois plus faible qu'avant.
De la même façon, si on marque l'air contenu dans les 500 premiers mètres
après le brassage et qu'on remonte les trajectoires individuelles des
particules fluides, ces particules avant le brassage proviennent
avec une équiprobabilité des deux premiers kilomètres. Le rétro-polluant
subit donc exactement la même dilution avant le brassage que le polluant
direct après. On retrouve bien que, pour une même injection, polluant direct
dans ![]() et rétro-polluant dans
et rétro-polluant dans ![]() ont la même concentration.
ont la même concentration.
Définie de cette façon, la réciprocité s'étend facilement à des puits et sources linéaires. Dans ce cas, l'échange n'est plus régit uniquement par le taux d'échange d'air comme dans le cas conservatif. Il faut tenir compte de la création ou de la destruction de traceur le long des trajectoires.
Dans le cas d'un radio-élément avec un taux de décroissance
![]() ,
si le même taux de décroissance est appliqué pour les transports direct
et inverse, la même concentration
,
si le même taux de décroissance est appliqué pour les transports direct
et inverse, la même concentration
Ce résultat s'étend en fait facilement à n'importe quel puits
linéaire, pour lequel le taux de décroissance
![]() peut varier dans l'espace et dans le temps (réaction
chimique avec un composant très peu affecté par la réaction
en question, paramétrisations simples du lessivage par les pluies, ...)
4.1.
Dans ce cas, la concentration
peut varier dans l'espace et dans le temps (réaction
chimique avec un composant très peu affecté par la réaction
en question, paramétrisations simples du lessivage par les pluies, ...)
4.1.
Dans ce cas, la concentration ![]() peut s'exprimer de façon générale
comme
peut s'exprimer de façon générale
comme
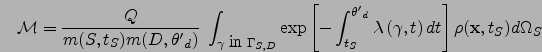 au niveau du détecteur. Pour
au niveau du détecteur. Pour
On peut calculer ![]() en intégrant vers le futur l'équation d'advection
en intégrant vers le futur l'équation d'advection
De façon symétrique, on peut calculer ![]() en intégrant vers le passé
l'équation de rétro-transport
en intégrant vers le passé
l'équation de rétro-transport
La symétrie du transport atmosphérique peut alors s'écrire formellement comme
Du fait de la linéarité du transport, les équations ci-dessus s'étendent
également à des émissions ![]() et mesures
et mesures ![]() non locales,
que ce soit dans le temps ou dans l'espace.
non locales,
que ce soit dans le temps ou dans l'espace.
Si on récrit à présent les équations ci-dessus sous forme de
relations entre sources et concentrations,
![]() et
et
![]() ,
la réciprocité du transport atmosphérique se résume alors à la relation
,
la réciprocité du transport atmosphérique se résume alors à la relation
![]() .
Ceci établit, sur des bases physiques, que les équations pour le
transport direct et rétro sont adjointes l'une de l'autre
(ou que les opérateurs
.
Ceci établit, sur des bases physiques, que les équations pour le
transport direct et rétro sont adjointes l'une de l'autre
(ou que les opérateurs ![]() et
et ![]() sont adjoints l'un de l'autre)
pour le produit scalaire pondéré par la masse de l'air
sont adjoints l'un de l'autre)
pour le produit scalaire pondéré par la masse de l'air
On utilise ici l'approche adjointe pour aboutir par un autre chemin aux résultats de la section précédente. On en profite pour traiter un cas un peu plus général.
On considère une mesure de concentration de la forme
La méthode adjointe fournit une approche générale pour expliciter
le lien entre une observable quelconque (ici ![]() ) et n'importe quel
paramètre d'entrée (ici la source, la concentration
initiale et l'apport de traceurs aux frontières du domaine).
Voici comment se décline la méthode.
) et n'importe quel
paramètre d'entrée (ici la source, la concentration
initiale et l'apport de traceurs aux frontières du domaine).
Voici comment se décline la méthode.
L'Eq. 4.5 est introduite dans l'expression de la mesure
4.9 :
Si on transforme par intégration par partie la partie advective de
l'Eq. 4.10:
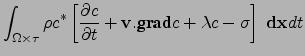 , qui peut être transformée en forme advective en utilisant
l'équation de continuité pour l'air :
, qui peut être transformée en forme advective en utilisant
l'équation de continuité pour l'air :
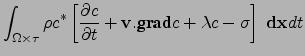 la solution de l'Eq. 4.6, avec la condition
que
la solution de l'Eq. 4.6, avec la condition
que 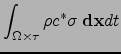 ), on obtient finalement
), on obtient finalement
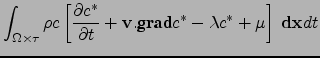 , du flux rentrant de traceur à la frontière
, du flux rentrant de traceur à la frontière
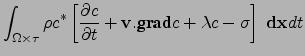 qui s'avère être identique au
rétro-traceur introduit précédemment
4.3.
Dans le cas où l'atmosphère est initialement dépourvue de traceur et
en l'absence d'apport latéral, l'expression (4.15) de la
mesure (4.9) se réduit au dernier terme, ce qui complète la démonstration
mathématique de la relation de symétrie (4.7) établie précédemment
sur la base de considérations cinématiques.
qui s'avère être identique au
rétro-traceur introduit précédemment
4.3.
Dans le cas où l'atmosphère est initialement dépourvue de traceur et
en l'absence d'apport latéral, l'expression (4.15) de la
mesure (4.9) se réduit au dernier terme, ce qui complète la démonstration
mathématique de la relation de symétrie (4.7) établie précédemment
sur la base de considérations cinématiques.
A noter qu'avec la même algèbre, on montre que, pour un traceur conservatif
(![]() et
et
![]() ),
et pour des instants compris strictement entre émission et mesure, on a
),
et pour des instants compris strictement entre émission et mesure, on a
| (4.16) |
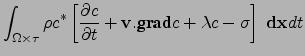 au même instant de l'air qui sera
échantillonné plus tard par le détecteur.
au même instant de l'air qui sera
échantillonné plus tard par le détecteur.
Dans le cas d'un traceur conservatif (![]() ), la partie homogène
de l'équation de transport (4.5)
), la partie homogène
de l'équation de transport (4.5)
La réciproque est également vraie.
La preuve découle d'une succession de transformations élémentaires de la
dérivée temporelle de la quantité conservée
Dans le cas de l'advection pure, la concentration massique du traceur ![]() est conservée pour n'importe quel élément de masse
est conservée pour n'importe quel élément de masse
![]() . De ce fait, la quantité
. De ce fait, la quantité
![]() est conservée dans le temps.
On obtient donc l'identité des équations directe et adjointe du transport
pour le produit scalaire pondéré par la masse d'air
comme un cas particulier du résultat de Talagrand et Courtier (1987).
est conservée dans le temps.
On obtient donc l'identité des équations directe et adjointe du transport
pour le produit scalaire pondéré par la masse d'air
comme un cas particulier du résultat de Talagrand et Courtier (1987).
Dans les dérivations algébriques présentées précédemment,
c'est la présence de la densité de l'air ![]() dans la
seconde intégrale de l'Eq. 4.10 qui permet de tirer avantage de la conservation
de la masse
(4.13) pour obtenir la symétrie exacte entre
les équations 4.6 et 4.5.
dans la
seconde intégrale de l'Eq. 4.10 qui permet de tirer avantage de la conservation
de la masse
(4.13) pour obtenir la symétrie exacte entre
les équations 4.6 et 4.5.
On a déjà vu plus haut que, pour des raisons pratiques à la fois de connaissance observationnelle du champ de vent et de limitation de puissance des ordinateurs, on ne considère généralement l'Eq. 4.5 que jusqu'à une certaine échelle spatiale (dite grande échelle ou échelle explicite), l'effet des échelles inférieures à la coupure (échelles turbulentes, ou sous-maille pour les modèles) sur les échelles explicites étant représenté au travers de paramétrisations. Le mélange turbulent, particulièrement actif dans la couche limite planétaire, va en général disperser le traceur dans un volume d'air plus grand et faire décroître les concentrations. De façon symétrique, avec davantage de brassage, le détecteur échantillonnera un air provenant d'une origine plus étendue mais avec une sensibilité moindre aux sources. On voit donc que l'image de diffusion turbulente doit être associée dans le monde rétro à une diffusion vers le passé et que cette diffusion est d'autant plus grande que la diffusion directe est importante. C'est ce qui est illustré sur le schéma B de la Fig. 4.1.
Dans la Section 2.2, on a établit la séparation d'échelle
pour le transport atmosphérique à partir de la notion de moyenne d'ensemble.
On a ainsi obtenu pour l'équation d'advection,
Le même traitement peut être appliqué à l'équation du rétro-transport
en changeant simplement le signe du vent
On montre ci-dessous comment le flux turbulent
![]() peut être obtenu pour différentes paramétrisations classiques, à la fois
sur des bases physiques et au travers de la méthode adjointe.
peut être obtenu pour différentes paramétrisations classiques, à la fois
sur des bases physiques et au travers de la méthode adjointe.
Les paramétrisations en diffusion turbulente sont basées sur l'image du brassage par des mouvements montants et descendants symétriques (comme précédemment, et par soucis de simplification de la présentation, nous nous limitons à la composante verticale du mélange turbulent). Quand on inverse le transport, la turbulence consiste encore en des mouvements montants et descendants symétriques qui ont donc le même effet de diffusion sur le traceur rétro.
Pour les modèles Lagrangiens prenant en compte la composante turbulente à l'aide de perturbations aléatoires des trajectoires, la même marche aléatoire doit être appliquée sur les rétro-trajectoires (Vautard et al., 2001; Flesch et al., 1995).
Dans le formalisme Eulérien, il faut revenir à l'image sous-tendant
les formulations en diffusion. Dans l'approche en longueur de mélange
(Prandtl et Tietjens, 1934),
la concentration du traceur ![]() pour une réalisation
donnée de l'écoulement et pour un mouvement descendant, est représentative
de la concentration moyenne de l'air à une distance
pour une réalisation
donnée de l'écoulement et pour un mouvement descendant, est représentative
de la concentration moyenne de l'air à une distance ![]() (longueur de mélange) au dessus.
On a donc,
(longueur de mélange) au dessus.
On a donc,
![]() pour les mouvements descendants
(
pour les mouvements descendants
(![]() ) et
) et
![]() dans les ascendances,
ce qui aboutit, dans les deux cas, à
dans les ascendances,
ce qui aboutit, dans les deux cas, à
![]() .
C'est ainsi qu'on aboutit au flux turbulent
.
C'est ainsi qu'on aboutit au flux turbulent
| (4.24) |
Le même traitement peut être appliqué au flux turbulent de rétro-traceur,
à ceci près que, puisque le traceur est advecté
à rebours le long des trajectoires, on associera à une valeur
positive de ![]() une concentration de rétro-traceur représentative
de l'air situé au-dessus, de sorte que
une concentration de rétro-traceur représentative
de l'air situé au-dessus, de sorte que
| (4.26) |
Dans de nombreuses applications, on est amené à considérer des traceurs
émis ou déposés à la surface.
Dans ce cas, les sources et puits associés sont généralement traités
comme une condition aux limites du modèle de diffusion turbulente
Pour interpréter une mesure, en intégrant à rebours les équations du rétro-transport, aucune source ne doit être ajoutée au rétro-traceur (conservation de la masse d'air). La condition aux limites pour le rétro-traceur est donc un flux nul en surface. Puisque l'émission va rajouter du traceur dans l'air, près de la surface, on peut aussi se convaincre que le rétro-traceur donnera également la sensibilité à l'émission de surface. Les résultats concernant la diffusion turbulente et les conditions en surface peuvent également être obtenus au travers de la méthode adjointe comme suit.
Nous récrivons à nouveau la mesure ![]() en introduisant l'équation de
transport
en introduisant l'équation de
transport
| (4.31) | |||
![$\displaystyle \int_{\Omega\times\tau} \rho c^* \left[\frac{\partial c}{\partial...
...rtial z}
\left(\rho K_z \frac{\partial c}{\partial z}\right)\right] {\bf dx}dt$](img1036.png) |
(4.32) |
Le terme de diffusion verticale subit une double intégration par
partie qui le transforme en
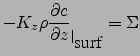 |
![$\displaystyle \left[c^* \rho K_z\frac{\partial c}{\partial z}\right]_{\mbox{surf}}^\infty$](img1038.png) |
||
| (4.33) |
En prenant pour le traceur adjoint (ou rétro) la solution de
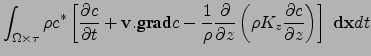 |
(4.34) | ||
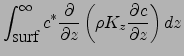 |
(4.35) | ||
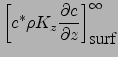 |
(4.36) |
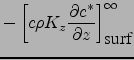 |
(4.37) |
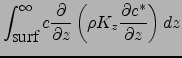 est le domaine de l'intégration horizontale)
comme somme des contributions de la concentration initiale et
de l'émission en surface.
est le domaine de l'intégration horizontale)
comme somme des contributions de la concentration initiale et
de l'émission en surface.
Cette démonstration confirme les résultats obtenus à partir des considérations
physiques concernant la symétrie de la diffusion turbulente. On voit aussi
que la distribution d'origine de l'air (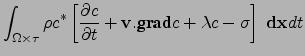 ) fournit les sensibilités
à la fois aux conditions initiales et aux émissions en surface.
) fournit les sensibilités
à la fois aux conditions initiales et aux émissions en surface.
On montre ici comment le rétro-transport peut être étendu aux paramétrisations de la convection. On s'intéresse particulièrement au schéma de convection nuageuse de Tiedtke (1989) et au modèle du thermique mais la même approche peut s'appliquer sans grande difficulté à d'autres schémas comme celui d'Emanuel (1991).
On considère donc le cas où la colonne convective est séparée en trois
compartiments
(se reporter au schéma (a) de la Fig. 4.2).
On reprend les notations des chapitres précédents.
L'ascendance est caractérisée par un flux de masse
![]() , exprimé en kg m
, exprimé en kg m![]() s
s![]() .
L'échange d'air entre l'ascendance et l'environnement est prescrit au
travers d'un taux d'entraînement
.
L'échange d'air entre l'ascendance et l'environnement est prescrit au
travers d'un taux d'entraînement 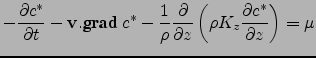 et d'un détraînement
et d'un détraînement
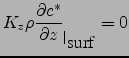 (tous deux en kg m
(tous deux en kg m![]() s
s![]() ).
La descente précipitante (seulement dans le cas de Tiedtke) est caractérisée
par un flux
).
La descente précipitante (seulement dans le cas de Tiedtke) est caractérisée
par un flux 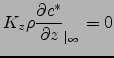 , un entraînement
, un entraînement ![]() et un détraînement
et un détraînement ![]() .
.
On rappelle que, sous des hypothèses de stationnarité,
l'équation de continuité pour l'air s'écrit, dans l'ascendance
La concentration du traceur dans les deux colonnes convectives est donnée
par
Le flux de masse turbulent est finalement paramétrisé sous la forme suivante
La même paramétrisation peut être appliquée en mode rétro-transport en inversant la direction du mouvement vertical dans les sous-colonnes et le sens des transferts. La transformation est schématisée sur la partie (b) de la Fig. 4.2. En intégration à rebours, l'air est par exemple transporté vers le bas rapidement dans l'ascendance, et l'entraînement direct à la base de la colonne convective joue alors le rôle d'un détraînement. La subsidence lente dans l'environnement est pour sa part remplacée par une ascendance lente.
Pour un profil de traceur 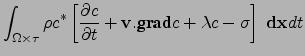 du modèle de rétro-transport,
les concentrations de rétro-traceur dans l'ascendance (
du modèle de rétro-transport,
les concentrations de rétro-traceur dans l'ascendance (![]() )
et la descente précipitante (
)
et la descente précipitante (![]() ) sont solutions de
) sont solutions de
Finalement, le modèle en flux de masse du rétro-transport
(Eqs. 4.43 à 4.45)
se déduit du modèle direct
(Eqs. 4.40 à 4.42) en remplaçant
(![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 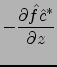 ,
, ![]() ,
, ![]() ,
, ![]() )
par
(
)
par
(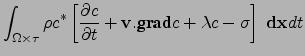 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ).
En pratique, pour passer
d'une intégration directe à une intégration à rebours, il suffit
de remplacer dans le code numérique
(
).
En pratique, pour passer
d'une intégration directe à une intégration à rebours, il suffit
de remplacer dans le code numérique
(![]() ,
, ![]() ,
, ![]() ,
, ![]() )
par
(
)
par
(![]() ,
, ![]() ,
, ![]() ,
, ![]() ),
), ![]() et
et ![]() étant recalculés par les
Eqs. (4.38) et (4.39), et
étant recalculés par les
Eqs. (4.38) et (4.39), et ![]() et
et 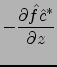 (ou
(ou ![]() et
et ![]() pour le rétro-transport) étant des variables internes
de la paramétrisation.
pour le rétro-transport) étant des variables internes
de la paramétrisation.
Il est à noter que ce modèle de rétro-transport convectif a été utilisé dans le modèle LMDZ (Hourdin et Issartel, 2000) bien avant d'obtenir la démonstration algébrique présentée ci-dessous. Siebert et Frank (2003) sont arrivés à des conclusions similaires concernant l'inversion du traitement du transport par la convection nuageuse dans un cadre Lagrangien.
Pour la dérivation mathématique, et afin d'éviter les lignes de
calculs inutiles, on se restreint à un modèle composé d'une ascendance
concentrée et d'une subsidence compensatoire comme pour le modèle du
thermique
(
![]() ).
).
Le modèle du transport direct pour un traceur conservatif s'écrit alors
En suivant encore une fois la même approche, on récrit la mesure ![]() comme
comme
| (4.47) | |||
| (4.48) | |||
| (4.49) |
On récrit l'intégrale
| (4.50) |
| (4.51) |
![\begin{displaymath}
I=\int_{\mbox{surf}}^\infty c^* \left[\hat{d}(c-\hat{c}) -\h...
...{\partial \hat{c}}{\partial z}+\hat{e}(\hat{c}-c) \right] dz
\end{displaymath}](img1072.png) |
(4.52) |
![\begin{displaymath}
I=\int_{\mbox{surf}}^\infty c \left[\hat{d}c^*+\frac{\partia...
...rtial \hat{f}\hat{c}^*}{\partial z}+\hat{e}\hat{c}^*\right] dz
\end{displaymath}](img1073.png) |
(4.53) |
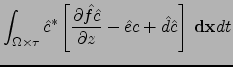 la solution de l'Eq. 4.43,
la mesure s'écrit finalement
la solution de l'Eq. 4.43,
la mesure s'écrit finalement
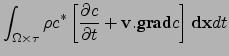 |
(4.54) | ||
![$\displaystyle \int_{\Omega}\left[\rho c^* c\right]_{t_i}^{t_f} \delta_x
-\int_\tau \left[\rho{\bf v}c^* c.{\bf n}\right]_{\partial \Omega } dt$](img992.png) |
(4.55) | ||
![$\displaystyle \int_{\Omega\times\tau} \rho c \left[\frac{\partial c^*}{\partial...
...artial \hat{f}\left({\hat{c}}^*-c^*\right)}{\partial z}+\mu\right]
{\bf dx}dt$](img1075.png) |
(4.56) |
En prenant pour 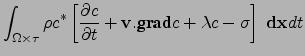 la solution de
la solution de
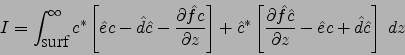 |
(4.57) |
Il est à remarquer que sans la démarche physique exposée plus haut, il aurait été facile de dériver un modèle adjoint à partir de cette méthode systématique, mais que l'équation obtenue in fine aurait pu différer de la forme symétrique obtenue ici, et qui permet d'utiliser le même algorithme dans les deux modes d'intégration.
Pour les formulations en matrices d'échange, qui sont directement dérivées dans le monde numérique, on peut appliquer directement la réciprocité en terme de coefficient d'échange et inverser simplement les rôles de la maille d'origine et de la maille de destination du traceur.
Les développements présentés ci-dessus ont été mis en ![]() uvre dans LMDZ.
uvre dans LMDZ.
Les intégrations à rebours dans le temps sont évidemment effectuées uniquement en mode débranché. Il n'est en aucun cas question ici d'inverser la météorologie elle-même.
On obtient finalement le mode rétro à partir du mode direct débranché dont
les équations complètes s'écrivent
| (4.60) |
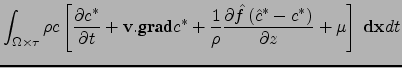 |
(4.61) |
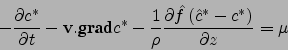 |
(4.62) |
On montre ici une illustration et un test numérique de la symétrie du transport atmosphérique en utilisant à nouveau le contexte de la campagne ETEX-1.
La colonne de gauche de la Fig. 4.3
montre l'évolution temporelle simulée de la concentration
de surface pour une émission de
340 kg de PMCH à Monterfil, entre ![]() et
et 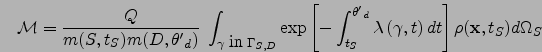 h.
La source est repérée par un cercle sur les figures.
24 heures après l'émission, le panache atteint la station allemande D05,
repérée par des carrés sur les mêmes figures.
La concentration maximum est obtenue à cette station à
h.
La source est repérée par un cercle sur les figures.
24 heures après l'émission, le panache atteint la station allemande D05,
repérée par des carrés sur les mêmes figures.
La concentration maximum est obtenue à cette station à ![]() +36h.
Dans la colonne de droite, on montre les résultats d'une simulation
à rebours, pour laquelle les 340 kg de PMCH sont injectés à la
station D05 de façon régulière entre
+36h.
Dans la colonne de droite, on montre les résultats d'une simulation
à rebours, pour laquelle les 340 kg de PMCH sont injectés à la
station D05 de façon régulière entre ![]() h et
h et ![]() h.
La réciprocité du transport est illustrée par le fait que la même concentration
est observée dans le carré 36 heures après l'émission pour la simulation
directe (carte en bas à gauche de la Fig. 4.3 montrant la moyenne de la concentration
directe entre
h.
La réciprocité du transport est illustrée par le fait que la même concentration
est observée dans le carré 36 heures après l'émission pour la simulation
directe (carte en bas à gauche de la Fig. 4.3 montrant la moyenne de la concentration
directe entre ![]() et
et ![]() h) et dans le cercle au moment de l'injection
réelle pour
la simulation à rebours (panneau en haut à droite montrant la
rétro-concentration moyenne entre
h) et dans le cercle au moment de l'injection
réelle pour
la simulation à rebours (panneau en haut à droite montrant la
rétro-concentration moyenne entre 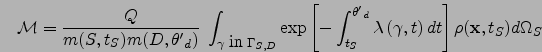 h et
h et ![]() ).
La Fig. 4.4 montre les coupes verticales correspondantes le long d'un
transect reliant la source et la station.
On voit sur la figure que le panache est advecté plus rapidement dans sa
partie supérieure. C'est la combinaison du transport horizontal par
un vent cisaillé et du mélange vertical par la turbulence qui explique
la dispersion rapide du panache et du rétro-panache dans un plan horizontal.
).
La Fig. 4.4 montre les coupes verticales correspondantes le long d'un
transect reliant la source et la station.
On voit sur la figure que le panache est advecté plus rapidement dans sa
partie supérieure. C'est la combinaison du transport horizontal par
un vent cisaillé et du mélange vertical par la turbulence qui explique
la dispersion rapide du panache et du rétro-panache dans un plan horizontal.
A droite : FMTs pour les 11 stations retenues pour les études d'intercomparaison de modèles. On montre les FMTs mesurant l'écart entre simulation directe et observation pour le schéma I de Van Leer et pour le schéma de Godunov, ainsi que les FMTs mesurant l'écart entre simulation directe et reconstitution inverse pour ces deux schémas. |
La partie de gauche de la
Fig. 4.5 montre la comparaison entre les estimations directe et
rétro de l'évolution temporelle de la concentration de PMCH
pour la station D05 ainsi que les observations.
Ici, le PMCH est injecté de façon uniforme entre
![]() et
et ![]() h comme dans la réalité et on considère la moyenne
des concentrations sur 3 heures.
De façon symétrique, on considère la moyenne sur les 12 heures d'injection
de rétro-panaches émis toutes les 3 heures.
Avec le schéma I de Van Leer, les simulations directe (carrés noirs)
et rétro (signes +) diffèrent, mais la différence est moindre qu'entre
chacune des simulations et les observations.
Les petites différences entre estimations directe et rétro proviennent
en fait pour l'essentiel de la violation de la symétrie du transport
par les limiteurs de pentes introduits dans le schéma de Van Leer pour garantir
positivité et monotonie.
Avec le schéma de Godunov (carrés blancs et étoiles) en effet, les simulations
directe et rétro sont presque confondues à la précision de la figure.
h comme dans la réalité et on considère la moyenne
des concentrations sur 3 heures.
De façon symétrique, on considère la moyenne sur les 12 heures d'injection
de rétro-panaches émis toutes les 3 heures.
Avec le schéma I de Van Leer, les simulations directe (carrés noirs)
et rétro (signes +) diffèrent, mais la différence est moindre qu'entre
chacune des simulations et les observations.
Les petites différences entre estimations directe et rétro proviennent
en fait pour l'essentiel de la violation de la symétrie du transport
par les limiteurs de pentes introduits dans le schéma de Van Leer pour garantir
positivité et monotonie.
Avec le schéma de Godunov (carrés blancs et étoiles) en effet, les simulations
directe et rétro sont presque confondues à la précision de la figure.
Ce comportement est confirmé par le calcul des FMTs pour les 11
stations privilégiées
pour les analyses ETEX (se reporter à la Section 2.6 pour plus de détails
sur l'analyse des simulations directes).
La simulation directe avec le schéma I de Van Leer comparé
aux observations (carrés noirs) montre un FMT moyen
de 40![]() environ alors que, pour le même schéma,
les FMTs mesurant l'écart entre estimations directe et
rétro pour le schéma I de Van Leer dépassent toujours 75
environ alors que, pour le même schéma,
les FMTs mesurant l'écart entre estimations directe et
rétro pour le schéma I de Van Leer dépassent toujours 75![]() (cercles noirs).
La différence entre estimation directe et rétro est bien plus faible
quand on utilise le schéma de Godunov
(ronds blancs, avec un FMT moyen de 98,2
(cercles noirs).
La différence entre estimation directe et rétro est bien plus faible
quand on utilise le schéma de Godunov
(ronds blancs, avec un FMT moyen de 98,2![]() ).
Enfin, la symétrie est quasiment exacte quand on inverse l'ordre d'appel
aux différents modules de transport dans le calcul rétro (signes +,
FMT moyenne de 99,5%) comme on l'explique plus loin.
).
Enfin, la symétrie est quasiment exacte quand on inverse l'ordre d'appel
aux différents modules de transport dans le calcul rétro (signes +,
FMT moyenne de 99,5%) comme on l'explique plus loin.
On étudie ci-dessous systématiquement la symétrie des algorithmes
utilisés dans LMDZ. Dans le modèle, l'advection, la diffusion turbulente,
la convection et la décroissance radioactive sont appelées de façon
séquentielle. L'intégration du modèle peut donc être vue comme une succession
de pas de transition entre un champ de concentration ![]() et
et
![]() , un pas de temps étant une succession particulière de tels pas.
Nous allons considérer la symétrie de chaque pas individuel en comparant
l'algorithme de rétro-transport obtenu à partir de transformations
simples sur le modèle direct (changement de signe et permutation des flux de
masse pour la convection par exemple) et l'adjoint du code numérique.
, un pas de temps étant une succession particulière de tels pas.
Nous allons considérer la symétrie de chaque pas individuel en comparant
l'algorithme de rétro-transport obtenu à partir de transformations
simples sur le modèle direct (changement de signe et permutation des flux de
masse pour la convection par exemple) et l'adjoint du code numérique.
Il faut donc, pour discuter en détail ces aspects numériques, introduire
l'adjoint d'un code numérique.
La définition mathématique de l'opérateur adjoint est la suivante.
Soient ![]() et
et ![]() deux espaces de Hilbert munis de deux produits scalaires
deux espaces de Hilbert munis de deux produits scalaires
![]() et
et
![]() , et soit
, et soit
![]() un opérateur de
un opérateur de ![]() dans
dans ![]() , l'adjoint
, l'adjoint
![]() de
de ![]() est un opérateur de
est un opérateur de ![]() dans
dans ![]() défini par la relation
défini par la relation
| (4.68) |
Etant donné un produit scalaire discrétisé au pas ![]() ,
,
![]() ,
où
,
où ![]() est une matrice symétrique définie positive, l'adjoint
du modèle numérique direct permet de calculer
l'évolution à rebours dans le temps
du gradient
est une matrice symétrique définie positive, l'adjoint
du modèle numérique direct permet de calculer
l'évolution à rebours dans le temps
du gradient ![]() d'une fonction objective quelconque
d'une fonction objective quelconque ![]() par rapport aux variables d'état du modèle
(cf. e. g. Talagrand et Courtier, 1987).
Ceci se montre simplement par comparaison des expressions du gradient
aux pas
par rapport aux variables d'état du modèle
(cf. e. g. Talagrand et Courtier, 1987).
Ceci se montre simplement par comparaison des expressions du gradient
aux pas
![]() et
et ![]()
Pour le produit scalaire canonique, ![]() , on trouve le résultat classique :
, on trouve le résultat classique :
![]() .
.
Le produit scalaire pondéré par la masse de l'air correspond à
![]() où
où
![]() est la masse d'air dans la maille
est la masse d'air dans la maille ![]() .
Si on prend comme convention d'indiçage
.
Si on prend comme convention d'indiçage
![]() ,
on trouve, pour les éléments des matrices directe et adjointe, la relation
,
on trouve, pour les éléments des matrices directe et adjointe, la relation
Si le modèle de transport est linéaire, pour tout pas de temps ![]() entre la
source et la détection, une mesure linéaire de
entre la
source et la détection, une mesure linéaire de ![]() peut être évaluée
comme
peut être évaluée
comme
![]() , qui, pour
, qui, pour
![]() , est un équivalent numérique de l'Eq. 4.17.
, est un équivalent numérique de l'Eq. 4.17.
La symétrie du code numérique est donc équivalente à
l'identité entre le mode rétro-transport ![]() du modèle direct
du modèle direct ![]() (obtenu
pour LMDZ par la transformation
(obtenu
pour LMDZ par la transformation
![]() )
et l'opérateur adjoint du modèle numérique direct.
La symétrie sera donc testée au moyen de la relation
(4.74)
(ou (4.75)) avec
)
et l'opérateur adjoint du modèle numérique direct.
La symétrie sera donc testée au moyen de la relation
(4.74)
(ou (4.75)) avec ![]() .
.
Pour des paramétrisations linéaires qui ne modifient pas la densité
de l'air - c'est le cas par exemple de la diffusion
turbulente, de la convection, ou de l'advection par un champ de vent non divergent -
c'est à dire dans le cas où
![]() ,
il est plus commode de tester une version légèrement modifiée des relations
(4.74) ou (4.75) en écrivant le modèle
sous une forme intégrale comme
,
il est plus commode de tester une version légèrement modifiée des relations
(4.74) ou (4.75) en écrivant le modèle
sous une forme intégrale comme
| (4.75) |
La même relation ![]() garantit en fait plus généralement
la symétrie du schéma
garantit en fait plus généralement
la symétrie du schéma
| (4.78) | |||
| (4.79) |
![$\displaystyle {\left[I-\left(1-\gamma\right)M^{-1}A^T\right]}^{-1} \left[I+\gamma M^{-1}A^T\right]
\cstnp1$](img1149.png) |
(4.80) |
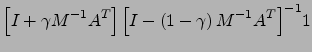 étant remplacée par
étant remplacée par
Les courbes relatives au schéma de Godunov sur la Fig. 4.5 suggèrent que le schéma de Godunov est symétrique, ce que nous démontrons ci-dessous.
Considérons dans un premier temps le cas de l'advection unidimensionnelle
avec un champ
de vent non divergent ![]() , une grille régulière de pas
, une grille régulière de pas ![]() et un pas de temps
et un pas de temps ![]() .
Si on note
.
Si on note
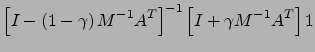 le nombre de Courant,
l'évolution de la concentration du traceur pour la maille
le nombre de Courant,
l'évolution de la concentration du traceur pour la maille ![]() est
donnée dans le schéma de Godunov par
est
donnée dans le schéma de Godunov par
| (4.81) |
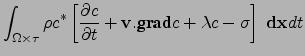 avec le vent
avec le vent | (4.82) |
La symétrie
du transport est également vérifiée pour un champ de vent non divergent.
Si on note ![]() le transfert de masse entre les mailles
le transfert de masse entre les mailles
![]() et
et ![]() et les instants
et les instants ![]() et
et ![]() et si on suppose - pour fixer les idées - que ce transfert est positif,
le schéma amont s'écrit
et si on suppose - pour fixer les idées - que ce transfert est positif,
le schéma amont s'écrit
| (4.85) |
| (4.86) |
| (4.87) |
Comme on l'a expliqué plus haut (Section 2.3),
le passage en dimension 3 est effectué dans le modèle au moyen
d'un calcul successif dans les 3 directions, successivement en
![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() avec un pas de temps deux fois plus petit dans
les deux directions horizontales.
Dans chaque direction,
l'Eq. 4.85 pour le traceur et
l'Eq. 4.86 pour l'air sont intégrées simultanément.
Ceci assure la symétrie du schéma tridimensionnel.
avec un pas de temps deux fois plus petit dans
les deux directions horizontales.
Dans chaque direction,
l'Eq. 4.85 pour le traceur et
l'Eq. 4.86 pour l'air sont intégrées simultanément.
Ceci assure la symétrie du schéma tridimensionnel.
On voit donc une fois de plus que le schéma amont de Godunov présente
beaucoup de bonnes propriétés (positivité, monotonie, diminution de la
variation totale, linéarité, et maintenant
symétrie) mais au prix d'une diffusion numérique importante.
On a déjà vu dans la Section 2.3.4 que le schéma de Godunov peut se récrire
Les schémas en volumes finis plus sophistiqués, comme le schéma I de Van Leer, peuvent souvent aussi être décrits comme la somme d'un schéma centré et d'un terme de diffusion, introduit pour éviter les oscillations numériques ou la dispersion. Cependant, ce terme de diffusion dépend alors en général de la concentration du traceur (elle est plus active là où le traceur montre de brusques variations de concentration), rompant la linéarité et donc la symétrie du schéma.
Le cas particulier du schéma de Van Leer et les implications pour l'utilisation pour l'inversion du transport sont discutées plus loin.
Pour la diffusion turbulente, on utilise dans le modèle LMDZ
un schéma implicite en temps et centré sur la verticale :
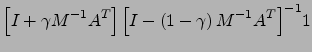 étant donnée par
étant donnée par
| (4.91) | |||
| (4.92) | |||
| (4.93) |
Les schémas en flux de masse utilisés dans le modèle sont également symétriques, mais c'est un peu plus fastidieux à démontrer. Comme précédemment, on va se restreindre au cas d'une ascendance compensée par une subsidence dans l'environnement.
Comme on l'a déjà expliqué au Chapitre 2,
les équations de continuité pour l'air et le traceur dans l'ascendance
(resp. Eqs. 4.68
et 4.66) sont discrétisées comme
| (4.95) |
L'évolution temporelle de la concentration grande échelle de traceur
restreinte au transport convectif, obtenue en combinant
les Eqs. 4.60 et 4.65 avec ![]() ,
, ![]() ,
,
![]() et
et
![]() , qui s'écrit
, qui s'écrit
| (4.96) |
| (4.97) | |||
| (4.98) |
Ce schéma est de la forme (4.76).
Puisque le modèle est linéaire, les éléments de la matrice 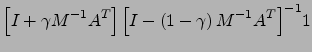 peuvent
être obtenus en calculant
peuvent
être obtenus en calculant
![]() dans la couche
dans la couche ![]() pour un traceur injecté dans
la couche
pour un traceur injecté dans
la couche ![]() (
(
![]() ).
).
Si on calcule d'abord les concentrations dans l'ascendance, pour cette
injection particulière, on trouve, pour ![]() ,
, ![]() .
Pour la couche d'injection, la concentration dans l'ascendance est donnée par
.
Pour la couche d'injection, la concentration dans l'ascendance est donnée par
| (4.99) |
Pour ![]()
| (4.100) |
| (4.101) |
| (4.102) |
| (4.103) |
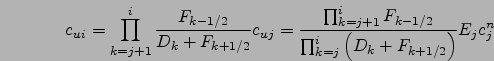 )
d'où l'on tire
)
d'où l'on tire
| (4.104) |
Le schéma pour le rétro-transport est obtenu en inversant le rôle de
![]() et
et 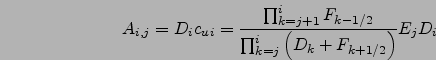 et en changeant le sens vertical de la propagation des
indices.
Le schéma rétro est donc également de la forme
(4.76), la matrice
et en changeant le sens vertical de la propagation des
indices.
Le schéma rétro est donc également de la forme
(4.76), la matrice 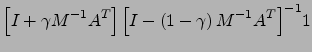 étant remplacée par la matrice
étant remplacée par la matrice ![]() dont les
éléments sont obtenus en considérant
une rétro-injection dans la couche
dont les
éléments sont obtenus en considérant
une rétro-injection dans la couche ![]() , ce qui donne
, ce qui donne
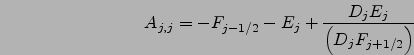 |
(4.105) | ||
| (4.106) | |||
| (4.107) |
En utilisant l'équation de continuité
(4.96), on vérifie que
![]() ce qui montre que les transports convectifs
adjoint et rétro sont identiques.
ce qui montre que les transports convectifs
adjoint et rétro sont identiques.
Les puits linéaires conservent aussi la masse d'air et peuvent être
discrétisés au moyen de la matrice diagonale
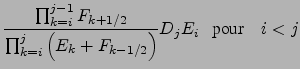 qui assure évidemment la symétrie.
qui assure évidemment la symétrie.
Dans le modèle direct, l'advection de grande échelle, la diffusion turbulente et le transport convectif sont traités de façon séquentielle. Si on veut vraiment obtenir la symétrie numérique avec le schéma de Godunov, il faut inverser complètement l'ordre de cette séquence dans le modèle. On ne le fait pas en standard dans le mode rétro de LMDZ qui utilise de toutes façons le schéma I de Van Leer, non symétrique.
C'est la non inversion de
cet ordre des opérateurs qui explique la différence résiduelle
entre calcul direct et rétro dans le cas où on utilise le schéma
de Godunov (cercles blancs sur la partie de droite de la Fig. 4.5).
Comme on l'a déjà dit, si on inverse cette séquence dans le calcul
rétro
(signes ![]() ), le FMT moyen pour les 11 stations passe
de 98,2 à 99,5%.
), le FMT moyen pour les 11 stations passe
de 98,2 à 99,5%.
Lorsque la discrétisation ne préserve pas la symétrie du transport, on a le choix pour les applications entre l'algorithme adjoint ou l'algorithme de rétro-transport. Les possibles implications sont illustrées et discutées dans le cadre de calculs d'advection unidimensionnelle avec le schéma de Van Leer.
Pour l'advection unidimensionnelle par un champ de vent non divergeant ![]() ,
sur une grille régulière, l'évolution temporelle de la concentration
du traceur dans la maille
,
sur une grille régulière, l'évolution temporelle de la concentration
du traceur dans la maille ![]() est donnée par
est donnée par
Dans le schéma I de Van Leer, la pente est d'abord calculée par différences
finies avant d'appliquer un limiteur de pente de sorte que
le calcul de la pente peut s'écrire sous la forme de la séquence d'opérations
et de tests suivante :
Partie B. Fonction d'influence à l'instant initial pour une mesure effectuée au pas de temps 30 (colonne de gauche) ou 150 (colonne de droite). Pour chaque graphique, la courbe épaisse continue montre la distribution de mesure. Les autres courbes montrent la sensibilité calculée avec l'algorithme de rétro-transport (courbe épaisse grise), avec l'adjoint du code direct (croix) et par perturbations de simulations directes (carrés). Les différents cas (de haut en bas) diffèrent par la distribution initiale de traceur ou par le schéma utilisé pour l'advection. | ||||||||||||||||||||||||||||||||||||
Nous montrons ci-dessous les résultats obtenus avec trois méthodes différentes pour calculer la sensibilité d'une mesure par rapport à la distribution initiale de traceur. Les deux premières méthodes consistent en l'intégration à rebours de l'algorithme de rétro-transport ou de l'algorithme adjoint. Le troisième calcul est obtenu par des perturbations successives de l'état initial suivies de simulations directes. Cette méthode requière autant d'intégrations que de points de grille.
La même méthode de perturbation a aussi été testée avec le modèle linéaire tangent. Comme il se doit, les résultats obtenus ainsi sont identiques à ceux de l'intégration adjointe et ces résultats ne sont donc pas montrés.
Pour un modèle linéaire et symétrique en temps, les trois estimations de la sensibilité doivent être égales. Ce point a été vérifié avec le schéma de Godunov (résultats non montrés). Pour un algorithme non symétrique mais linéaire, l'estimation par perturbations et l'estimation adjointe sont identiques mais diffèrent du calcul de rétro-transport. A cause des limiteurs de pentes (4.113, 4.115 et 4.116), le schéma I de Van Leer n'est pas linéaire. Dans ce cas, les trois estimations sont différentes. L'estimation par rétro-transport ne dépend que de la distribution de mesure alors que l'intégration adjointe dépend du calcul de base au voisinage duquel on calcule les sensibilités. Quant au calcul direct par perturbation, il dépend à la fois de la solution de base et de l'amplitude de la perturbation initiale. A cause des non-linéarités, l'intégration de l'adjoint du modèle nécessite le stockage de la solution de base qui est ensuite relue et utilisée pour activer les propositions conditionnelles dans les calculs (dans 4.113, 4.115 et 4.116) au cours du calcul de sensibilité.
Les résultats sont montrés sur la Fig. 4.6. Le domaine est périodique avec 60 points et on a choisi un nombre de Courant 0,2. Trois distributions initiales de traceurs sont testées : pas de traceur (état plat) ainsi qu'une onde sinusoïdale et une distribution carrée, toutes deux d'amplitude 1. Les deux graphiques du haut de la figure (partie A) montrent la distribution initiale et les résultats de l'intégration directe de base au pas de temps 150 pour les distributions sinusoïdale (à gauche) et carrée (à droite). La solution exacte de l'advection au pas 150 est une translation de =30 points de grille.
La partie B de la même figure montre des calculs de sensibilité
ou fonctions d'influence.
La mesure consiste en un prélèvement uniforme sur un intervalle de
6 points de grille.
La distribution de mesure correspondante (i. e. la fonction ![]() de
l'Eq. 4.9) correspond à la courbe noire épaisse sur tous les graphiques.
La sensibilité est calculée par rapport à la concentration initiale de traceur
pour une mesure effectuée au pas de temps 30 (pour la colonne de gauche)
et 150 (colonne de droite).
La sensibilité exacte serait obtenue en translatant la distribution de mesure
de -6 et -30 points respectivement.
Pour l'estimation directe, une perturbation d'amplitude
de
l'Eq. 4.9) correspond à la courbe noire épaisse sur tous les graphiques.
La sensibilité est calculée par rapport à la concentration initiale de traceur
pour une mesure effectuée au pas de temps 30 (pour la colonne de gauche)
et 150 (colonne de droite).
La sensibilité exacte serait obtenue en translatant la distribution de mesure
de -6 et -30 points respectivement.
Pour l'estimation directe, une perturbation d'amplitude ![]() est ajoutée successivement à chaque point de grille.
est ajoutée successivement à chaque point de grille.
Pour le cas 1 (graphiques du haut de la partie B), qui correspond
à un état initial sans traceur, la
condition (4.113) n'est jamais satisfaite.
La pente est donc nulle dans le calcul adjoint, qui équivaut alors
à un calcul avec le schéma de Godunov
(Eqs 4.110, 4.111 et 4.112 avec
).
La sensibilité correspondante est beaucoup plus diffuse que celle
obtenue avec l'algorithme rétro ou le calcul par perturbations,
ces deux derniers étant à la fois plus proches l'un de l'autre et plus proche
de la solution exacte.
Ce cas classique, où l'on essaie de reconstituer
une source en partant d'une concentration supposée nulle a priori,
est en fait ici un cas limite singulier dans lequel la sensibilité
dépend de choix arbitraires sur l'écriture du schéma.
En changeant le signe en ![]() dans
l'Eq. 4.113, on obtiendrait par exemple des sensibilités différentes.
dans
l'Eq. 4.113, on obtiendrait par exemple des sensibilités différentes.
Le cas 2, qui correspond à une onde sinusoïdale, est moins pathologique. Pour un pas de temps donné, la condition (4.113) est satisfaite presque partout et le limiteur de pentes est actif seulement pour un petit nombre de points de grille. Les trois estimations de la sensibilité sont affectées par la diffusion numérique mais sont relativement proches les unes des autres (celle calculée par rétro-transport, qui ne dépend que de la distribution de mesure, est la même que dans le cas 1). A noter que les estimations directes par perturbations et adjointes produisent de faibles valeurs négatives (on le voit particulièrement pour la sensibilité d'une mesure effectuée au pas de temps 150).
Le cas 3 correspond à une distribution carrée. La sensibilité calculée
par rétro-transport est à nouveau la même que précédemment.
Pour une mesure au pas 30, la solution adjointe commence à montrer des
oscillations numériques alors que les deux autres restent proches l'une de
l'autre. Pour une mesure au pas 150, les intégrations adjointes et par
perturbations produisent des oscillations bien plus grandes que le signal
lui-même avec des sensibilités négatives très importantes.
L'instabilité rencontrée ici peut être expliquée de la façon suivante.
Après un certain nombre de pas de temps pour la simulation directe,
la distribution n'est plus vraiment carrée mais décroît rapidement de
part et d'autre du pic de traceur,
typiquement par un ordre de grandeur d'un point de grille au suivant.
De ce fait, en amont du pic, dans la région où le pic de la sensibilité
est advecté (dans notre cas particulier), la condition 4.116
est atteinte partout.
Du coup, le schéma adjoint correspond en fait à un schéma direct associé
à une pente
![]() .
Ce schéma est pathologique comme schéma de transport à la fois parce
que l'estimation de la pente est systématiquement décentrée et parce que
cette pente est double d'une estimation classique par différences finies.
.
Ce schéma est pathologique comme schéma de transport à la fois parce
que l'estimation de la pente est systématiquement décentrée et parce que
cette pente est double d'une estimation classique par différences finies.
Afin d'illustrer ce cas plus en détail, on montre, dans la partie
de gauche de la Fig. 4.7,
les sensibilités directes calculées pour une mesure au pas 150 (comme
pour la partie de droite de la Fig. 4.6)
mais en utilisant différentes valeurs pour ![]() (rappelons que les
résultats montrés dans la Fig. 4.6 correspondent tous à
(rappelons que les
résultats montrés dans la Fig. 4.6 correspondent tous à ![]() ).
Pour des valeurs petites de
).
Pour des valeurs petites de ![]() , comme on peut s'y attendre, les résultats
sont proches du calcul adjoint.
Quand
, comme on peut s'y attendre, les résultats
sont proches du calcul adjoint.
Quand ![]() croît, les calculs directs par perturbations tendent à se lisser
et deviennent plus proches de la solution obtenue par rétro-transport (ainsi
que de la solution physiquement correcte).
Olivier Talagrand a proposé
l'explication suivante pour ce phénomène intéressant.
A cause de la présence des opérations conditionnelles associées aux limiteurs
de pentes (4.115) et (4.116),
chaque intégration du modèle direct traverse une série de bifurcations.
Pour des valeurs de perturbations suffisamment petites, la séquence
des bifurcations n'est pas modifiée (une petite perturbation
n'est pas ``vue" par le limiteur) et le calcul adjoint montre que la sensibilité
ainsi obtenue est très grande.
Quand on fait croître l'amplitude de cette perturbation, la séquence
des bifurcations est de plus en plus modifiée, avec des fluctuations très fortes
dans la sensibilité. Ces fluctuations tendent à s'annuler les unes les autres,
ce qui n'est pas surprenant dans la mesure où les limiteurs de pentes
sont justement introduit pour garantir le bon comportement physique
du schéma de transport.
Il est remarquable que le rétro-transport (qui inclue bien sûr les
limiteurs de pente) atteint le même but pour un coût bien moindre.
croît, les calculs directs par perturbations tendent à se lisser
et deviennent plus proches de la solution obtenue par rétro-transport (ainsi
que de la solution physiquement correcte).
Olivier Talagrand a proposé
l'explication suivante pour ce phénomène intéressant.
A cause de la présence des opérations conditionnelles associées aux limiteurs
de pentes (4.115) et (4.116),
chaque intégration du modèle direct traverse une série de bifurcations.
Pour des valeurs de perturbations suffisamment petites, la séquence
des bifurcations n'est pas modifiée (une petite perturbation
n'est pas ``vue" par le limiteur) et le calcul adjoint montre que la sensibilité
ainsi obtenue est très grande.
Quand on fait croître l'amplitude de cette perturbation, la séquence
des bifurcations est de plus en plus modifiée, avec des fluctuations très fortes
dans la sensibilité. Ces fluctuations tendent à s'annuler les unes les autres,
ce qui n'est pas surprenant dans la mesure où les limiteurs de pentes
sont justement introduit pour garantir le bon comportement physique
du schéma de transport.
Il est remarquable que le rétro-transport (qui inclue bien sûr les
limiteurs de pente) atteint le même but pour un coût bien moindre.
Le cas 4 correspond aussi à une distribution initiale carrée, mais l'intégration
est effectuée avec le second schéma de Van Leer, déjà décrit dans la
Section 2.3.6, dans lequel la pente
(4.114) est remplacée par
![]() .
Dans ce cas, les conditions
4.115 et 4.116 ne sont jamais atteintes.
Ce schéma est légèrement plus diffusif que le schéma I mais son comportement
est moins pathologique car sa non-linéarité est moins forte.
On observe encore cependant le même effet que pour le cas précédent bien
que dans une moindre mesure.
Pour
.
Dans ce cas, les conditions
4.115 et 4.116 ne sont jamais atteintes.
Ce schéma est légèrement plus diffusif que le schéma I mais son comportement
est moins pathologique car sa non-linéarité est moins forte.
On observe encore cependant le même effet que pour le cas précédent bien
que dans une moindre mesure.
Pour ![]() et à la précision de la figure, la sensibilité
adjointe et celle obtenue par perturbation sont confondues.
Pour
et à la précision de la figure, la sensibilité
adjointe et celle obtenue par perturbation sont confondues.
Pour ![]() , la sensibilité directe est en revanche plus proche du calcul
par rétro-transport.
, la sensibilité directe est en revanche plus proche du calcul
par rétro-transport.
D'autres résultats (non montrés) confirment que le calcul de rétro-transport fournit en générale une bonne estimation de la sensibilité calculée par perturbation du calcul direct avec des perturbations de relativement grande amplitude.
|
On voit que dans le cas où la sensibilité de l'algorithme direct est définie de manière non ambiguë, le calcul adjoint en fournit, comme il se doit, une bonne estimation. Cependant, pour des algorithmes fortement non-linéaires, cette estimation, exacte d'un point de vue numérique, peut s'avérer non physique (oscillations, valeurs négatives). En comparaison, le calcul par rétro-transport, robuste et préservant la positivité (ainsi que la monotonie), fournit des sensibilités qui restent réalistes et proches de la solution exacte même pour des schémas fortement non linéaires.
On compare à présent les différentes approches dans le contexte de l'assimilation variationnelle, a priori plus favorable au calcul adjoint, avec pour but de reconstruire la distribution initiale de traceur à partir d'observations distribuées dans le temps.
On effectue des tests académiques classiques de type ``expériences jumelles",
standards pour l'évaluation des algorithmes d'assimilation.
On commence par effectuer une simulation de référence, notée
![]() , sur
, sur ![]() pas de temps. Cette expérience est considérée comme
la réalité à reconstruire.
Des observations synthétiques sont générées à chaque pas de temps
pas de temps. Cette expérience est considérée comme
la réalité à reconstruire.
Des observations synthétiques sont générées à chaque pas de temps ![]() à partir de cette simulation
sous la forme
à partir de cette simulation
sous la forme
![]() , où
, où ![]() est à nouveau
la distribution de mesure.
Pour toute solution
est à nouveau
la distribution de mesure.
Pour toute solution ![]() de l'équation de transport, la fonction
objective (scalaire)
de l'équation de transport, la fonction
objective (scalaire)
La minimisation est effectuée grâce au code M1QN3 développé par Gilbert et Lemaréchal (1989). Il s'agit d'une procédure itérative qui nécessite, à chaque pas, au moins une approximation du gradient de la fonction objective. L'algorithme est de type quasi-Newtonien, ce qui signifie que le gradient local est utilisé pour bâtir petit à petit une approximation de l'inverse du Hessien (matrice des dérivées secondes) de la fonction objective. L'utilisation de cet inverse rend la minimisation particulièrement efficace, au moins dans le cas où le gradient varie de façon relativement douce.
Deux séries d'expériences ont été effectuées ici, en utilisant, pour calculer le gradient, dans le premier cas l'adjoint exact du modèle direct et dans le second cas l'adjoint approché obtenu par rétro-transport.
Dans toutes les expériences, effectuées dans le même cadre unidimensionnel
que pour la
section précédente, la longueur de la simulation de référence est
de ![]() pas de temps, ce qui correspond à une révolution complète sur
le domaine d'advection. La fonction de mesure est également comme avant
un prélèvement uniforme sur 6 points de grille (courbe épaisse discontinue
sur la Fig. 4.8).
Avec ces choix, le minimum de la fonction objective est unique et égal
à zéro.
pas de temps, ce qui correspond à une révolution complète sur
le domaine d'advection. La fonction de mesure est également comme avant
un prélèvement uniforme sur 6 points de grille (courbe épaisse discontinue
sur la Fig. 4.8).
Avec ces choix, le minimum de la fonction objective est unique et égal
à zéro.
b : Evolution de l'erreur d'estimation des états initial et final de l'intervalle d'assimilation. c : Concentrations initiales ``réelle" et reconstituée à la fin de la minimisation. d : Les mêmes états que pour le graphique c mais au pas de temps |
Les résultats sont présentés sur la Fig. 4.8.
L'état initial de la simulation de référence utilisé comme réalité correspond
à la distribution carrée déjà utilisée précédemment (courbe épaisse sur
les graphiques du bas).
On utilise le schéma I de Van Leer. La minimisation est initiée à partir
d'un état sans traceurs.
La minimisation est poursuivie jusqu'à ce que la décroissance de la
fonction objective entre deux états successifs de la minimisation soit
plus petite qu'un seuil prescrit.
Le graphique a) montre que, comme on peut s'y attendre, la minimisation
aboutit à une valeur plus faible de la fonction objective quand on calcule
le gradient avec l'adjoint exact plutôt qu'avec l'algorithme de rétro-transport.
Cependant, la minimisation est plus rapide au début avec le rétro-transport.
La reconstruction de la concentration initiale (graphique c)
est également très légèrement meilleure avec l'algorithme de rétro-transport
(ce qui se voit aussi sur l'erreur quadratique moyenne montrée
sur le graphique b).
En fait, si les deux reconstructions obtenues en fin de minimisation
diffèrent à l'instant initial, elles
sont en revanche quasiment identiques au pas d'advection ![]() (graphique d).
C'est ici la diffusion numérique qui rend difficile la reconstruction de l'état
initial, et qui explique que les oscillations de l'état initial (graphique
c) ne soit pas ``vues" par les mesures.
Le même effet se produirait dans la réalité avec la diffusion turbulente.
(graphique d).
C'est ici la diffusion numérique qui rend difficile la reconstruction de l'état
initial, et qui explique que les oscillations de l'état initial (graphique
c) ne soit pas ``vues" par les mesures.
Le même effet se produirait dans la réalité avec la diffusion turbulente.
D'autres résultats (non montrés) confirment les résultats obtenus ici à savoir que la minimisation est généralement plus poussée avec l'adjoint mais plus rapide au début avec l'algorithme de rétro-transport. Les différences concernant la reconstruction de l'état initial sont souvent non significatives, mais à nouveau, cette reconstruction est souvent légèrement meilleure avec l'algorithme de rétro-transport. Ces résultats sont cohérents avec ceux présentés sur la Fig. 4.7. Le gradient approché mais lisse obtenu avec l'algorithme de rétro-transport permet une localisation imparfaite mais rapide du minimum de la fonction objective. L'utilisation du gradient exact permet une localisation plus précise de ce minimum. Mais ce gain ne semble pas utile en pratique. De plus, dans certains cas (non montrés), ce gradient exact peut osciller tellement que la minimisation échoue.
On peut en tirer la conclusion que, au moins sur les exemples académiques présentés ici, l'utilisation d'un gradient certes approché, mais lisse et présentant un bon comportement physique, est préférable à l'utilisation d'un gradient exact mais présentant de fortes oscillations.
Nous avons bien sûr appliqué cette approche à l'évaluation de l'efficacité des réseaux TICE (Hourdin et Issartel, 2000).
Les réseaux développés pour la vérification du TICE ont été dimensionnés a priori pour pouvoir détecter des essais d'une kt équivalent TNT partout sur la planète. Comme on l'a déjà dit dans l'introduction de ce chapitre, la détection et la localisation des évènements suspects reposera sur la mesure d'ondes se propageant depuis le lieu de l'explosion : mesures sismiques pour des tirs souterrains, mesure d'ondes infra-sonores pour les essais atmosphériques et hydroacoustiques pour les essais sous-marins. Le quatrième réseau - celui qui nous intéresse ici - mesurera en 80 stations la radioactivité atmosphérique associée aux aérosols. 40 de ces 80 stations seront en plus équipées d'instrument mesurant la concentration en isotopes du xénon. Alors que les isotopes radioactifs se fixant sur des aérosols ne sont relâchés que dans le cas d'essais atmosphériques, le xénon, gaz noble non soluble dans l'eau, est a priori émis également en quantité appréciable lors d'essais sous-marins ou souterrains (De Geer, 1996).
Avec une demi-vie de 5,2 jours, le ![]() Xe est l'isotope le plus important du
xénon loin des sources. Le comité d'experts en charge de la définition
des réseaux TICE a estimé qu'un essai nucléaire de 1 kt doit
relâcher environ
Xe est l'isotope le plus important du
xénon loin des sources. Le comité d'experts en charge de la définition
des réseaux TICE a estimé qu'un essai nucléaire de 1 kt doit
relâcher environ ![]() Bq si il est aérien ou sous-marin
et environ 10 fois moins pour un essai souterrain
(le xénon s'échappant alors par des failles, Carrigan et al., 1996).
A partir de ces chiffres, un seuil de détection de 1 mBq m
Bq si il est aérien ou sous-marin
et environ 10 fois moins pour un essai souterrain
(le xénon s'échappant alors par des failles, Carrigan et al., 1996).
A partir de ces chiffres, un seuil de détection de 1 mBq m![]() a été
retenu comme spécification pour les mesure de xénon.
Pour parvenir à cette sensibilité, les détecteurs prélèvent de l'air sur une
journée entière avec des pompes puissantes pour effectuer une mesure.
a été
retenu comme spécification pour les mesure de xénon.
Pour parvenir à cette sensibilité, les détecteurs prélèvent de l'air sur une
journée entière avec des pompes puissantes pour effectuer une mesure.
Nous sommes arrivés dans la boucle des discussions avant que le choix des
40 stations du sous-réseau ne soit définitivement arrêté. Grâce à l'approche
inverse présentée ci-dessus, et à sa mise en ![]() uvre dans LMDZ,
nous avons pu
alors produire des cartes globales d'efficacité de détection du réseau
pour les différents choix de sous réseaux (note interne CEA).
uvre dans LMDZ,
nous avons pu
alors produire des cartes globales d'efficacité de détection du réseau
pour les différents choix de sous réseaux (note interne CEA).
Nous présentons ci-dessous les résultats du calcul d'efficacité du réseau xénon pour la détection des essais souterrains où sous-marins et pour la configuration finalement retenue pour le réseau xénon.
Dans ce cas particulier, la symétrie du calcul est totale.
Au lieu d'effectuer les tirs aux stations et de les détecter au niveau des
détecteurs, on injecte dans le modèle les 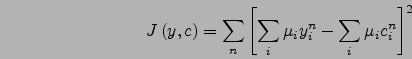 Bq à l'ensemble des
40 détecteurs (un traceur par détecteur)
à un instant donné.
Si on s'intéresse à une détection ayant lieu le 14 juillet par exemple,
on injecte le traceur au détecteur uniformément pendant la journée.
On intègre le modèle à l'envers en
tenant compte d'une décroissance radioactive avec une demi-vie de 5,2 jours.
Un essai effectué par exemple le 5 juillet sera détecté par
cette station le 15 si le rétro-panache émis le 15 à la station dépasse le 5
le seuil de détection des appareils à l'endroit où le tir est effectué.
pour tenir compte de la moindre source pour les essais souterrains, le
seuil est de 1 mBq m
Bq à l'ensemble des
40 détecteurs (un traceur par détecteur)
à un instant donné.
Si on s'intéresse à une détection ayant lieu le 14 juillet par exemple,
on injecte le traceur au détecteur uniformément pendant la journée.
On intègre le modèle à l'envers en
tenant compte d'une décroissance radioactive avec une demi-vie de 5,2 jours.
Un essai effectué par exemple le 5 juillet sera détecté par
cette station le 15 si le rétro-panache émis le 15 à la station dépasse le 5
le seuil de détection des appareils à l'endroit où le tir est effectué.
pour tenir compte de la moindre source pour les essais souterrains, le
seuil est de 1 mBq m![]() sur mer et seulement
sur mer et seulement ![]() mBq m
mBq m![]() sur
continents.
sur
continents.
Les simulations ont été effectuées avec le modèle LMDZ débranché en relisant les archives d'une simulation guidée en résolution 96x72x19 et en redécoupant chaque maille horizontale en 2x2 mailles pour obtenir une résolution de 1,9 pour le calcul du transport.
Les résultats sont montrés sur la Fig. 4.9. On montre d'abord sur la figure du haut les ``zones de visibilité" du réseau avec des délais de plus en plus grands pour une détection le 15 janvier 1991. Les stations du sous-réseau xénon sont repérées par des points verts. On reconnaît bien dans les tropiques sur les océans les régimes d'alizés avec une zone de visibilité confinée dans une bande relativement étroite à l'est des stations. L'étendue des zones détectées est beaucoup plus grande dans les moyennes latitudes. On voit qu'au bout de 14 jours, le réseau est loin de détecter l'ensemble de la surface du globe dans les tropiques. Le gain de détection est relativement faible entre les jours 10 et 14. De plus, dans les tropiques, les zones détectées sont alors souvent déconnectées des zones détectées plus tôt, ce qui indique qu'on détecte de l'air qui a recirculé dans la troposphère moyenne ou haute. C'est particulièrement clair dans le Pacifique tropical ou les détections au-delà de 10 jours proviennent de régions proches de l'équateur et correspondent donc à des traceurs ayant été emportés dans les cellules de Hadley avant de redescendre pour être détecté plus haut en latitude.
On effectue ensuite des statistiques à partir d'un ensemble de simulations pour des jours de détection différents. En pratique ici, on a effectué les statistiques à partir de 15 jours de détection, allant du 15 au 31 janvier dans un cas et du 15 au 31 juillet dans l'autre pour estimer les effets saisonniers. On voit clairement sur les graphiques A de la Fig. 4.9 que le réseau est insuffisant dans les tropiques, à la fois à cause de la relative étroitesse des zones détectées dans les régions d'alizés et parce qu'une bonne partie des traceurs est emportée dans la haute atmosphère par la circulation de Hadley. La détection est évidemment globalement plus faible pour les tirs souterrains. Les graphiques du bas montrent la redondance des mesures, c'est à dire le nombre de fois moyen où un essai va être détecté. On voit que le réseau ne montre une relative redondance que dans les moyennes latitudes, sur les océans.
D'autres calculs ont été effectuées, notamment des calculs pour le réseau aérosols qui montrent que ce réseau aura une très bonne capacité de détection, au problème près du lessivage, processus encore très mal connu et ne pouvant être représenté que de façon assez grossière dans les modèles (note interne CEA).
|
En cas de redondance des mesures, la question qui vient rapidement à l'esprit est de savoir s'il est possible de localiser les sources. De nombreuses approches existent pour combiner les rétro-panaches afin d'essayer de localiser les sources. Plus précisément dans le cadre du TICE, il s'agirait de déterminer la position, la date et l'intensité de la source.
La question est plus importante qu'il n'y paraît à première vue dans le cas du TICE. On a vu en effet que dans ce cas, la localisation devrait être effectuée par les réseaux sismiques, infra-sonores ou hydroacoustiques. Mais la question qui va se poser nécessairement, c'est l'interprétation de tous les évènements douteux, qui n'auront justement pas été enregistrés par les autres réseaux et pourront correspondre souvent à des incidents ou accidents nucléaires. En fait, la sensibilité du réseau xénon est telle que le nucléaire civile va être assez systématiquement enregistré aux stations xénon, même en période de fonctionnement normal.
Nous avons laissé cette question et l'étude des méthodes associées à nos collègues du CEA. Nous montrons cependant pour illustration un calcul de localisation de la source d'ETEX à partir de rétro-panaches. On suppose ici que la date et l'intensité de la source sont connues. On utilise les simulations à 9 des 11 stations ETEX étudiées précédemment (NL05, B05, NL01, D44, DK05, DK02, D05, PL04 et H02).
Pour n'importe quelle position possible de la source, on peut calculer
la moyenne des FMT (
![]() ) par rapport aux observations
réelles.
Une fois les rétro-panaches calculés, ce calcul est très peu coûteux
numériquement.
Le résultat est montré sur la Fig. 4.10.
L'estimation grossière qui consisterait à prendre comme lieu d'émission
le maximum de cette fonction objective donnerait une source située
dans la manche, éloignée d'environ 100 à 300 km du lieu réel d'émission.
) par rapport aux observations
réelles.
Une fois les rétro-panaches calculés, ce calcul est très peu coûteux
numériquement.
Le résultat est montré sur la Fig. 4.10.
L'estimation grossière qui consisterait à prendre comme lieu d'émission
le maximum de cette fonction objective donnerait une source située
dans la manche, éloignée d'environ 100 à 300 km du lieu réel d'émission.
Les mêmes cartes peuvent bien sûr être calculées pour n'importe quelle intensité de la source et n'importe quel instant d'émission. Le maximum de la fonction objective peut dans ce cas encore être estimé par une simple recherche du minimum absolu. Plus généralement, l'approche peut être appliquée à la détermination d'une source étendue à la fois dans le temps et dans l'espace. L'accroissement de la dimension du système peut alors nécessiter l'utilisation d'algorithmes de minimisation plus sophistiqués adaptés à des fonctions montrant des extrema locaux.
L'approche du rétro-transport peut également être utilisée pour inverser
des sources continues. Des travaux ont été entrepris dans ce sens
au LSCE (Peylin, 2005) dans le cadre du contrôle des émissions de
CO![]() .
Depuis un certain nombre d'années, des méthodes inverses sont utilisées
pour essayer de contraindre les puits et sources de CO
.
Depuis un certain nombre d'années, des méthodes inverses sont utilisées
pour essayer de contraindre les puits et sources de CO![]() à partir
de mesures de concentration à des stations de surface (Bousquet et Peylin, 2000).
La méthode utilisée jusque là consistait à effectuer des simulations
directes de transport avec des sources affectées à des grandes régions
(quelques dizaines au plus pour couvrir le globe).
Les concentrations ainsi simulées
étaient ensuite utilisées pour contraindre les puits et sources sur une base
mensuelle.
à partir
de mesures de concentration à des stations de surface (Bousquet et Peylin, 2000).
La méthode utilisée jusque là consistait à effectuer des simulations
directes de transport avec des sources affectées à des grandes régions
(quelques dizaines au plus pour couvrir le globe).
Les concentrations ainsi simulées
étaient ensuite utilisées pour contraindre les puits et sources sur une base
mensuelle.
Le travail entrepris avec l'approche rétro-transport vise à régionaliser
cette description des puits et sources en utilisant la partie
haute fréquence (synoptique dans un premier temps) des observations de CO![]() .
Dans le cas d'une source continue en surface, le rétro-transport
fournit un modèle paramétrique de la mesure
.
Dans le cas d'une source continue en surface, le rétro-transport
fournit un modèle paramétrique de la mesure
| (4.117) |
1. Ce qu'il faut stoker comme rétro-concentrations, ce sont des concentrations moyennes entre deux instants de stockages. Sous ces conditions, on retrouve une inversion exacte pour une source ne fluctuant pas dans le temps.
2. Si la source ![]() varie dans le temps, par exemple avec un cycle
diurne important, il est important d'échantillonner les variations
temporelles escomptées.
Si on n'échantillonne pas le cycle diurne au moment du stockage,
on va faire une erreur puisqu'on négligera la corrélation entre le
cycle diurne des coefficients d'échange (fortement influencé par le cycle
diurne de la couche limite) et le cycle diurne des sources (correspondant
par exemple à la respiration des plantes). On fera alors une erreur
systématique pouvant conduire à des biais importants dans l'inversion
(effet bien connu dans le cas des inversions des sources de
CO
varie dans le temps, par exemple avec un cycle
diurne important, il est important d'échantillonner les variations
temporelles escomptées.
Si on n'échantillonne pas le cycle diurne au moment du stockage,
on va faire une erreur puisqu'on négligera la corrélation entre le
cycle diurne des coefficients d'échange (fortement influencé par le cycle
diurne de la couche limite) et le cycle diurne des sources (correspondant
par exemple à la respiration des plantes). On fera alors une erreur
systématique pouvant conduire à des biais importants dans l'inversion
(effet bien connu dans le cas des inversions des sources de
CO![]() sous le vocable de rectifier effect).
sous le vocable de rectifier effect).
En revanche,
si on n'échantillonne pas la mesure - par exemple si on rétro-injecte tous les
jours une concentration de CO![]() correspondant à la moyenne mesurée pendant
cette journée - on perdra de l'information mais on ne fera pas d'erreur.
correspondant à la moyenne mesurée pendant
cette journée - on perdra de l'information mais on ne fera pas d'erreur.
3. Si on dispose de mesures sur une région relativement restreinte du globe, l'utilisation d'une grille zoomée sur cette région est sans doute relativement optimale. En effet, plus les sources sont distantes des mesures et moins on a besoin de précision sur le rétro-traceur ; moins on est sensible au détail de la répartition spatiale des sources. On peut donc tout à fait à la fois accepter une diffusion numérique importante liée à l'utilisation d'une grille grossière et également se contenter de stoker les rétro-panaches sur une grille grossière, choses que l'on fait naturellement avec une grille étirable.
Nous avons établi ici, pour des traceurs linéaires, l'exacte équivalence entre le transport rétro, défini à partir du suivi à rebours dans le temps des trajectoires atmosphériques, et du transport adjoint pour le produit scalaire pondéré par la masse de l'air.
Bien que mathématiquement équivalentes, ces deux approches correspondent à des visions relativement différentes. L'approche adjointe est un outil mathématique systématique, qui permet de calculer la sensibilité des sorties d'un modèle par rapport à des paramètres d'entrée. Le rétro-transport est une approche physique dans la quelle on peut appliquer dans un monde rétro- des approches physiques ou numériques utilisées d'habitude pour le transport atmosphérique direct. Le passage du monde direct au monde rétro ne requière en général qu'un nombre très restreint d'opérations.
Le fait de réaliser que le rétro-transport n'est pas restreint au monde Lagrangien des trajectoires atmosphériques permet de bénéficier de tous les outils développés ces dernières décennies, notamment concernant le transport turbulent dans la couche limite et la paramétrisation du transport convectif dans les nuages. Les formules en diffusion turbulente, basées sur des images de mouvement aléatoires symétriques, sont inchangées en mode rétro. En revanche, le rôle des ascendances et subsidences doit être interverti dans les formulations en flux de masses et on doit changer le rôle des origines et destinations dans les formulations en matrices d'échanges (ce qui revient à une transposition).
Quand on passe dans le monde numérique, l'équivalence entre transport adjoint et rétro n'est plus nécessairement assurée.
Nous avons montré, en comparant les algorithmes adjoint et rétro, que la symétrie était assurée dans LMDZ pour tous les processus de transport autres que l'advection, et, pour cette dernière, si on utilisait l'algorithme linéaire mais très diffusif de Godunov ou un schéma centré également linéaire, moins diffusif mais oscillant. Vukicevic et al. (2001), dans un articles sur des calculs académiques d'assimilation pour de l'advection bidimensionnelle, ont également remarqué que le schéma "QUICK", un peu plus sophistiqué mais toujours linéaire (et ne garantissant pas la positivité) était également symétrique.
La dérivation de schémas de plus en plus précis et garantissant un bon comportement physico-numérique (conservation, positivité, monotonie) conduit à des schémas non-linéaires. Dans ce cas, l'adjoint du code direct fournit une sensibilité qui dépend de la solution directe de base et est numériquement exact alors que l'utilisation en mode rétro de l'algorithme direct fournit une sensibilité approchée mais unique (ne dépendant pas du calcul direct) et présentant de bonnes propriétés physico-numériques. La positivité du schéma peut par exemple s'avérer essentielle pour certains algorithmes de localisation de rejets accidentels de polluants.
Des expériences numériques effectuées dans le contexte le plus simple possible de l'advection unidimensionnelle avec deux versions (non linéaires) du schéma de Van Leer suggèrent que le rétro-transport, du fait de sa robustesse et de la préservation de la positivité, peut être préférable à l'adjoint exact, même pour des algorithmes de minimisation classiques basés sur des descentes de gradients. Ce résultat est relativement important en pratique. Il avait été montré par le passé que des erreurs même faibles sur le calcul du gradient pouvaient conduire à une inhibition totale de la minimisation. Ceci n'est peut-être pas vrai si l'algorithme numérique repose sur des bases physiques suffisantes.
Enfin remarquons que, si la symétrie du transport présentée ci-dessus n'a de sens que pour des traceurs linéaires, le mode rétro de la partie transport peut être utilisé comme adjoint approché et couplé aux codes adjoints de processus non linéaires comme la chimie. Cette approche a d'ailleurs déjà été appliquées au LGGE à Grenoble à des inversions des mesures de concentrations en espèces soufrées pour des stations Antarctiques (Cosme, 2005).
Titan, le plus gros satellite de Saturne, possède comme la Terre une atmosphère
dense d'azote avec une pression en surface de 1,4 10![]() Pa. pour une
gravité de 1,35 m s
Pa. pour une
gravité de 1,35 m s![]() .
L'azote moléculaire (98% de la masse
de l'atmosphère) et le méthane (un peu moins de 2% au-dessus de la tropopause)
sont photo-dissociés
dans la haute atmosphère, entre 600 et 1000 km d'altitude, par
des électrons magnétosphériques ou des rayons ultra-violets.
Les radicaux ainsi formés
initient une photochimie complexe impliquant notamment des hydrocarbures
et des nitriles. Une vingtaine de molécules différentes ont été
identifiées à ce jour, soit par par la sonde américaine Voyager soit
par des observations depuis la Terre.
Des expériences de laboratoire suggèrent que des composés aussi
complexes que des ``ammono-équivalents" des acides aminés pourraient
être créés naturellement dans cette atmosphère (Raulin et Owen, 2002).
Celle-ci peut donc être vue comme une
expérience grandeur nature du développement d'une chimie complexe en l'absence
de vie (chimie pré-biotique).
.
L'azote moléculaire (98% de la masse
de l'atmosphère) et le méthane (un peu moins de 2% au-dessus de la tropopause)
sont photo-dissociés
dans la haute atmosphère, entre 600 et 1000 km d'altitude, par
des électrons magnétosphériques ou des rayons ultra-violets.
Les radicaux ainsi formés
initient une photochimie complexe impliquant notamment des hydrocarbures
et des nitriles. Une vingtaine de molécules différentes ont été
identifiées à ce jour, soit par par la sonde américaine Voyager soit
par des observations depuis la Terre.
Des expériences de laboratoire suggèrent que des composés aussi
complexes que des ``ammono-équivalents" des acides aminés pourraient
être créés naturellement dans cette atmosphère (Raulin et Owen, 2002).
Celle-ci peut donc être vue comme une
expérience grandeur nature du développement d'une chimie complexe en l'absence
de vie (chimie pré-biotique).
On pense que c'est la polymérisation de certains de ces nitriles ou hydrocarbures qui est à l'origine de l'épaisse couche de brume orange qui voile l'ensemble de la planète (illustration sur la Fig. 5.1a). Les détails de cette polymérisation sont encore loin d'être connus et des travaux expérimentaux et théoriques ont été menés sur ce sujet (Lebonnois et al., 2002; Coll et al., 1999; Wilson et Atreya, 2003; Tran et al., 2003). Lors du survol de Titan par Voyager 1, les fréquences des instruments embarqués n'avaient pas permis de percer cette couche de brume. Ceci a contribué à préserver une partie du mystère concernant Titan, son système climatique et sa surface. Cependant, grâce aux progrès de l'observation depuis le sol (optique adaptative, interférométrie) et à la mise en orbite du Hubble Space Telescope, il avait été possible récemment de cartographier la surface de Titan dans des fenêtres du proche infrarouge. Des observations récentes avaient également suggéré la présence de nuages dans la basse atmosphère.
L'atmosphère de Titan est également très intéressante d'un point de vue
dynamique. Avec un rayon de 2500 km, une période de rotation de 16 jours
terrestres (Titan est en phase bloquée autour de Saturne)
et des vents zonaux d'ouest de l'ordre de 100 à 150 m s![]() , la
stratosphère de Titan tourne environ 10 à 15 fois plus vite que la planète
solide.
Ce phénomène de superrotation, observé pour la première fois sur Vénus,
a été d'abord prédit pour Titan à la fois sur la base d'arguments
théoriques (Golitsyn, 1975) puis de simulations numériques
(Hourdin et al., 1995b) avant d'être récemment confirmé par l'observation
depuis le sol par différentes techniques.
, la
stratosphère de Titan tourne environ 10 à 15 fois plus vite que la planète
solide.
Ce phénomène de superrotation, observé pour la première fois sur Vénus,
a été d'abord prédit pour Titan à la fois sur la base d'arguments
théoriques (Golitsyn, 1975) puis de simulations numériques
(Hourdin et al., 1995b) avant d'être récemment confirmé par l'observation
depuis le sol par différentes techniques.
La sonde américaine Cassini, lancée vers le système de Saturne en 1995, s'est mise en orbite autour de cette planète au printemps 2004. Tout au long de sa mission, elle va utiliser Titan pour modifier son orbite. Ce sont des dizaines de survols qui vont pouvoir confirmer ou infirmer les travaux théoriques développés au cours des dernières décennies et à coup sûr révéler un grand nombre de phénomènes inattendus. Le premier survol, pourtant très lointain, à déjà permis d'observer des nuages morcelés avec des échelles de quelques dizaines de kilomètres, près du pôle sud en été, là où les observations depuis la Terre montraient un point brillant. Début 2005, la sonde européenne Huygens s'est détachée de Cassini (illustration sur la Fig. 5.1b) pour une descente de deux heures dans l'atmosphère de Titan. Cette mission, superbe réussite technologique et scientifique, a permis pour la première fois de prendre des photos sous la couche de brumes. Elle a révélé un paysage incroyablement familier, avec des réseaux de rivières, des îles et des rivages (Fig. 5.2). La préparation de cette mission a motivé, notamment en France sous l'impulsion de Daniel Gautier (LESIA) et François Raulin (LISA), ainsi que de Christopher P. McKay (NASA/Ames), le développement d'études théoriques et numériques concernant à la fois la chimie, la microphysique et la dynamique de l'atmosphère de Titan.
Ces efforts de modélisation ont été au départ développés séparément. A l'observatoire de Bordeaux puis au CESR à Toulouse, des chercheurs se sont intéressés à la modélisation de la photochimie gazeuse (Toublanc et al., 1995). Au SA à Paris, c'est une modélisation microphysique très originale qui a été développée : les particules formant la brume sont représentées, juste après leur formation, comme des particules sphériques s'agrégeant suivant un modèle dit en ``gouttes liquides". Deux particules sphériques coagulent pour donner une nouvelle particule sphérique, plus grosse. A partir d'un certain stade, les particules (appelés monomères) se collent les unes aux autres, aboutissant à des particules moins denses, pouvant prendre la forme de chaînes ou de flocons. Cabane et al. (1992) ont développé une modélisation de ce mode d'agrégation au travers d'une description fractale des aérosols. Une dimension fractale de 2 pour les particules de la brume permet de réconcilier une bonne partie des observations Voyager (Cabane et al., 1993; Rannou et al., 1995) - en particulier, les photons UV ``voient" les monomères alors que les photons infrarouges ``voient" plutôt les agrégats -. Enfin, au LMD, c'est un modèle de circulation générale atmosphérique qui a été développé à partir du modèle climatique aujourd'hui baptisé LMDZ (Hourdin et al., 1995b).
Or il est apparu peu à peu que dynamique, chimie et microphysique étaient intimement couplées. On savait déjà depuis Voyager que les espèces chimiques montrent des contrastes latitudinaux très marqués, avec des enrichissement d'un facteur 1.5 à 20 dans les latitudes polaires nord au moment du passage de la sonde, peu après l'équinoxe de printemps nord (Coustenis et Bézard, 1995). De même, les variations saisonnières de l'albédo global de Titan, enregistrées depuis la Terre, avaient été interprétées comme la signature de variations saisonnières de la répartition des brumes (Sromovsky et al., 1981). Des études préliminaires menées en rajoutant le transport méridien dans des modèles microphysiques (Hutzell et al., 1995) ou chimiques (Lebonnois et al., 2001) ont montré que le transport méridien par les grandes cellules de Hadley obtenues dans les simulations dynamiques (Hourdin et al., 1995b) était sans doute responsable de ces contrastes en composition. En parallèle, des calculs radiatifs ont montré que ces variations de la composition pouvaient avoir un impact non négligeable sur le bilan radiatif dans la stratosphère de Titan (Bézard et al., 1995).
Devant ces constats et en prévision de l'arrivée programmée de la mission Cassini-Huygens, nous avons alors décidé (sans doute vers 1996), avec Dominique Toublanc et Michel Cabane, de rassembler ces différents efforts de modélisation pour développer un modèle couplé dynamique-chimie-microphysique du climat de Titan. Les études sur la dynamique de l'atmosphère de Titan avaient été jusque-là menées au LMD avec le modèle de circulation tridimensionnel. Pour des raisons de coût numérique et tenant compte du fait que les observations existantes semblaient indiquer de faibles variations longitudinales de la température ou de la composition, une approche bidimensionnelle a été privilégiée. Le travail de couplage entre les différentes composantes du système a véritablement débuté en 1996 par l'inclusion de la composante aérosols dans le modèle de circulation générale du LMD, à l'occasion du post-doc de Pascal Rannou à la NASA (Rannou, 2004; Rannou et al., 2002). Les aspects chimiques ont été développés en collaboration entre le CESR et le LMD autour de la thèse de Sébastien Lebonnois (Lebonnois et al., 2003b,2001). Enfin une composante essentielle de ce travail a consisté à développer une paramétrisation des ondes planétaires. Les équations dynamiques du modèle bidimensionnel s'écrivent relativement facilement comme la restriction des équations primitives de la météorologie à la composante axi-symétrique de l'écoulement. Mais il devient alors nécessaire de paramétriser le transport méridien par la composante non axi-symétrique de l'écoulement, essentielle par exemple pour représenter le phénomène de superrotation atmosphérique. Ce travail a été réalisé en collaboration entre le LMD et l'Observatoire de Lisbone à l'occasion de la thèse de David Luz (Luz, 2003b,2003).
A noter qu'un travail de longue haleine comme celui-là a été facilité par la liberté qui nous a été donnée de travailler pendant plusieurs années sur ce sujet sans obtenir de résultats présentables. Il a fallu environ 6 ans, parfois laborieux, entre le début du Post-doc de Pascal Rannou et la première publication montrant des résultats d'une version couplée du modèle. C'est l'ensemble de ce travail qui est synthétisé ici en se focalisant sur les aspects relatifs au transport atmosphérique.
On commence par présenter (Section 5.2) les simulations tridimensionnelles pour expliquer le phénomène de superrotation et donner les grandes lignes de la circulation générale sur Titan. On présente ensuite le développement du modèle couplé chimie/microphysique/dynamique (Section 5.3), les couplages dynamique-composition (Section 5.4), et une étude récente sur l'explication des contrastes de concentration chimique dans la stratosphère (Section 5.5).
Golitsyn (1975) a été le premier à suggérer que l'atmosphère de Titan puisse être, comme celle de Vénus, en régime de superrotation.
Les contrastes latitudinaux de température reconstitués à deux altitudes
- à partir des
observations des branches P et Q d'une bande du méthane par le
spectromètre infrarouge IRIS embarqué sur Voyager - suggéraient également
la présence de vents zonaux intenses, sans pouvoir en déterminer la
direction.
L'équilibre du vent thermique - qui permet de calculer ces vents
à partir des variations du champ de température - s'exprime en effet, quand
on utilise comme coordonnée verticale
le logarithme de la pression normalisée
![]() ,5.1comme :
,5.1comme :
 |
(5.1) |
Une deuxième source d'information originale
est venue conforter cette information sur l'intensité des vents.
Lors de l'observation de l'occultation d'une étoile très brillante, et
sous réserve qu'un observateur soit placé très près du centre
théorique de l'occultation, il est possible d'observer un pic
de lumière, ou flash central, dû à la réfraction des rayons lumineux dans
l'atmosphère de la planète, sur l'ensemble du pourtour du disque.
L'atmosphère joue alors un peu le rôle d'une loupe. Pour peu que cette
atmosphère soit déformée, la tâche de lumière projetée sur la Terre
au centre de la zone d'ombre se transforme en une caustique.
Un observateur situé à proximité du centre de l'observation verra, suivant
sa position, un ou deux maxima de lumière. Un nombre suffisant d'observateurs
permettra de reconstituer la forme de la caustique, et, par suite, la
déformation de l'atmosphère de la planète.
C'est sur ce principe que l'observation par plusieurs dizaines d'observateurs
professionnels ou amateurs de l'occultation de l'étoile 28-Stgr par
Titan a permis de contraindre la forme de l'atmosphère de Titan
(Hubbard, 1993).
L'aplatissement relativement important indiquait également des vents
de 100 à 200 m s![]() . Les observations étaient
même suffisamment précises pour prédire une augmentation du vent depuis
l'équateur vers les hautes latitudes dans l'hémisphère d'hiver.
Mais, comme pour le calcul du vent gradient, ces observations
ne permettaient pas de contraindre la direction du vent.
. Les observations étaient
même suffisamment précises pour prédire une augmentation du vent depuis
l'équateur vers les hautes latitudes dans l'hémisphère d'hiver.
Mais, comme pour le calcul du vent gradient, ces observations
ne permettaient pas de contraindre la direction du vent.
Ce sont donc les arguments théoriques comme ceux développés par Golitsyn (1975), puis les résultats de simulations numériques de Titan (Hourdin et al., 1995b) ou de simulations obtenues dans des conditions idéalisées (Hourdin et al., 1992; Del Genio et al., 1993) qui ont prédit le caractère prograde de ces vents. Au début des années 90, quand les premières simulations ont commencé à tourner, et que se discutaient les paramètres d'entrée pour la sonde Huygens, il apparaissait difficilement imaginable de disposer de confirmation observationnelle du caractère prograde des vents avant l'arrivée de la mission.
C'était sans compter sur le développement des nouvelles techniques d'observation et l'imagination des observateurs. La direction du vent a donc finalement été confirmée à l'aide de différentes techniques très sophistiquées, permettant de combiner très grande résolution spatiale (pour résoudre au moins en quelques points le disque de Titan) et spectrale. Les vents sont déduits du décalage Doppler soit de raies d'émission de l'éthane ou de nitriles (Moreno, 2003; Kostiuk et al., 2001) soit du spectre réfléchi du Soleil (Luz, 2003a).
|
|
| ||||||||||||||||||
Après des tentatives plus ou moins abouties dans les années 70 et 80 (y compris au LMD, Tourte, 1984), c'est au début des années 90 que les modèles de circulation générale ont permis d'obtenir des simulations cohérentes du phénomène de superrotation atmosphérique (Hourdin et al., 1992; Del Genio et al., 1993).
L'adaptation d'un modèle de circulation atmosphérique aux conditions
d'une autre atmosphère de type tellurique, comme Mars ou Titan,
consiste principalement
à débrancher le cycle de l'eau et à modifier le code de transfert
radiatif (les codes de transfert doivent être beaucoup simplifiés
dans les modèles de circulation et les simplifications sont toujours
très dépendantes des conditions particulières rencontrées).
Dans ce qui suit, on présente des résultats obtenus avec deux versions
du modèle du LMD correspondant à deux codes radiatifs différents.
Dans le modèle de circulation de Titan, on a remplacé le code radiatif
d'origine par le code radiatif développé spécifiquement pour Titan par
Toon et al. (1989) pour la partie solaire (UV et IR) et McKay et al. (1989)
pour l'infrarouge thermique.
Dans les premières simulations, les variations latitudinales de la
composition n'étaient pas prises en compte et on se basait, pour calculer
les opacités, sur un profil type de composition et température.
Dans la seconde version, appelée modèle paramétrique, l'atmosphère
était idéalisée comme un gaz gris, dépendant de deux profondeurs optiques,
l'une pour le spectre solaire (
 )
et l'autre pour l'infrarouge thermique (
).
)
et l'autre pour l'infrarouge thermique (
).
Dans ces deux modèles, on représente en plus la conduction thermique dans le sol discrétisé en 11 couches, le mélange turbulent dans la couche limite et un ajustement convectif sec pour éliminer les instabilités convectives. Le code dynamique tridimensionnel est inchangé à quelques constantes près comme la gravité ou les constantes thermodynamiques du gaz atmosphérique.
Les premières simulations de la superrotation atmosphérique ont été obtenues avec la version paramétrique du modèle (Hourdin et al., 1992). Dans une première simulation, on essaie de simuler une planète A aussi proche que possible de la Terre. Pour ce faire, l'inertie thermique du sol est augmentée pour représenter l'effet d'un océan (sans circulation). La planète est un peu éloignée du Soleil pour compenser l'absence de diffusion dans l'atmosphère. Les valeurs numériques retenues pour les 19 paramètres du modèle sont données dans la Table 5.1. Le modèle est intégré pendant plusieurs années avec un cycle saisonnier. On montre sur les graphiques de gauche de la Fig. 5.3 les résultats obtenus avec ce modèle pour l'hiver sud. On reconnaît une grande cellule de Hadley trans-équatoriale avec subsidence dans l'hémisphère d'hiver. L'isotherme zéro, les températures maximales à l'équateur, ainsi que les contrastes latitudinaux pôle/équateur sont simulés de façon relativement réaliste malgré la simplicité du modèle. L'intensité du jet simulé est relativement réaliste et on observe des vents négatifs (alizés) dans les basses latitudes.
Les figures de droite montrent les résultats obtenus pour une planète B tournant 10 fois plus lentement, absorbant davantage le rayonnement solaire ( =0.9 au lieu de 0.1) et avec une obliquité nulle. On voit cette fois que la circulation méridienne moyenne est dominée par deux grandes cellules de Hadley s'étendant jusqu'aux pôles, et que l'atmosphère est pour l'essentiel en superrotation, avec un facteur environ 10 à 200 hPa. Sur les graphiques du bas, on montre le moment cinétique normalisé . La moyenne planétaire de ce moment cinétique vaut 1 pour une atmosphère au repos. On peut donc le considérer comme un index de superrotation. On voit la très grande différence entre le moment cinétique de la planète A, essentiellement dominé par la rotation de la surface de la planète, et celui de la planète B, très homogène en latitude dans la branche haute des cellules de Hadley.
Dans les simulations décrites ci-dessus, le mécanisme responsable de la création et du maintien de la superrotation atmosphérique est celui qu'avait proposé Gierasch (1975) pour expliquer la superrotation de Vénus. La circulation méridienne moyenne fait monter plus de moment cinétique dans les basses latitudes, là où le moment cinétique dans l'atmosphère est maximum, qu'elle n'en ramène vers la surface dans les hautes latitudes, là où il est plus faible (ce qui est illustré sur la partie du haut de la Fig. 5.4). La circulation moyenne dans une telle atmosphère produit donc en permanence un transport de moment cinétique vers le haut de l'atmosphère. Ce mécanisme va par exemple expliquer l'établissement de la superrotation à partir d'une atmosphère au repos. Pour une telle atmosphère, qui tourne en fait à la même vitesse que la planète solide, le moment cinétique est en effet beaucoup plus grand à l'équateur que dans les hautes latitudes.
La situation se complique un peu quand la superrotation s'établit. En effet, il y alors plus de moment cinétique transporté vers les hautes latitudes dans la branche haute des cellules que vers l'équateur près de la surface. Il va donc falloir trouver un mécanisme capable de transporter le moment cinétique contre ce transport net vers les pôles, afin de maintenir un excès de moment cinétique à l'équateur (cet excès est bien présent dans les simulations).
En accord avec ce qui avait été suggéré par Gierasch (1975) et Rossow (1979), ce sont des ondes planétaires qui effectuent ce transport dans les simulations. En fait, une atmosphère en équilibre du vent gradient mais dont le moment cinétique croîtrait avec la latitude serait dynamiquement instable (instabilité inertielle). Prenons un écoulement axi-symétrique en équilibre entre un vent zonal positif et une force de pression dirigée vers les pôles. Si on suppose que localement le moment cinétique croît avec la latitude, et qu'on déplace vers le pôle une particule d'air (ou plutôt un anneau, c'est à dire une particule d'air dans une vision axi-symétrique de la circulation) en conservant son moment cinétique (pour un anneau, le moment des forces de pression par rapport à l'axe des pôles est nul), celle-ci va tourner moins vite que l'environnement. La force centrifuge qui la retient vers les basses latitudes ne contrebalancera donc plus la force de pression et la particule partira plus loin vers les pôles. Dans les simulations présentées plus haut, on voyait se développer à la fois l'instabilité inertielle (légère inflexion de l'isocontour 1,4 sur la partie droite du graphique du haut de la Fig. 5.4) et l'instabilité barotrope. Un critère suffisant d'instabilité barotrope est qu'il existe un changement de signe de la dérivée latitudinale de la vorticité potentielle dans la région considérée (Kuo, 1949). L'instabilité inertielle peut également se traduire comme la présence d'un changement de signe de la vorticité elle-même. La vorticité obtenue pour la planète B (graphique du bas de la Fig. 5.4) montre effectivement des zones de changement de signe à la fois de la vorticité et de sa dérivée (régions hachurées).
Si on se place à une pression de 500 hPa, on voit que le transport vertical tend en permanence à renforcer le vent près du pôle et à le diminuer près de l'équateur. Cette circulation méridienne force donc en continu l'instabilité de l'écoulement moyen. Cette instabilité nourrit en retour des ondes planétaires qui transportent l'excès le moment cinétique vers l'équateur.
De façon très similaire, Del Genio et al. (1993) ont obtenu une superrotation en partant d'un modèle terrestre, en réduisant sa vitesse de rotation et en augmentant artificiellement la couverture nuageuse pour accroître l'absorption de rayonnement solaire. Là aussi, c'est le transport de moment cinétique par la circulation méridienne composée de grandes cellules de Hadley s'étendant de part et d'autre de l'équateur jusqu'aux pôles qui est responsable de la superrotation. Là aussi, les ondes planétaires associées à la présence d'instabilité barotrope dans l'écoulement moyen expliquent le transport vers l'équateur de moment cinétique dans la branche haute de la cellule de Hadley.
C'est en grande partie la moindre rotation de la planète qui permet à
la circulation de Hadley de s'étendre jusque aux pôles
(Del Genio et Suozzo, 1987; Hunt, 1979).
En effet, la rotation de la planète est responsable de la création de
jets d'ouest intenses (la conservation du moment cinétique d'une
parcelle partant au repos de l'équateur produit sur Terre un vent
de 135 m s![]() à 30 degrés de latitudes). La rotation de la planète
fait également que la force de Coriolis (ou plus généralement
la force centrifuge mentionnée plus haut) dirigée vers
l'équateur arrive à freiner efficacement le mouvement de l'air vers les pôles.
C'est cet effet qui explique que la circulation de Hadley est cantonnée
dans les régions tropicales sur Terre.
A l'extrémité des cellules de Hadley terrestres, c'est l'instabilité barocline
de l'écoulement moyen qui génère des ondes planétaires. A l'opposé
de la planète B, ces ondes vont transporter le moment cinétique
des tropiques vers les extra-tropiques.
Comparativement, la cellule de Hadley équateur-pôle de la planète B
apparaît comme un système fermé ne pouvant exporter
son moment cinétique vers d'autres latitudes.
C'est l'accumulation de moment cinétique dans les hautes latitudes qui
va être à l'origine de l'instabilité barotrope de l'écoulement.
à 30 degrés de latitudes). La rotation de la planète
fait également que la force de Coriolis (ou plus généralement
la force centrifuge mentionnée plus haut) dirigée vers
l'équateur arrive à freiner efficacement le mouvement de l'air vers les pôles.
C'est cet effet qui explique que la circulation de Hadley est cantonnée
dans les régions tropicales sur Terre.
A l'extrémité des cellules de Hadley terrestres, c'est l'instabilité barocline
de l'écoulement moyen qui génère des ondes planétaires. A l'opposé
de la planète B, ces ondes vont transporter le moment cinétique
des tropiques vers les extra-tropiques.
Comparativement, la cellule de Hadley équateur-pôle de la planète B
apparaît comme un système fermé ne pouvant exporter
son moment cinétique vers d'autres latitudes.
C'est l'accumulation de moment cinétique dans les hautes latitudes qui
va être à l'origine de l'instabilité barotrope de l'écoulement.
L'autre différence importante entre les deux planètes
(et c'est la même chose dans les simulations de Del Genio et al., 1993) est que la
stabilité accrue de l'atmosphère dans le cas de la superrotation
(imposée en diminuant
![]() dans notre cas
ou en rajoutant des nuages dans le modèle de Del Genio et al., 1993) permet
de diminuer les échanges turbulents verticaux et de découpler les
couches externes de l'atmosphère de la surface.
dans notre cas
ou en rajoutant des nuages dans le modèle de Del Genio et al., 1993) permet
de diminuer les échanges turbulents verticaux et de découpler les
couches externes de l'atmosphère de la surface.
Les premières simulations longues obtenues avec la version titanesque
du modèle de circulation ont également produit une superrotation
intense avec des vents d'ouest de l'ordre de la centaine
de mètres par seconde à l'équateur, bien supérieurs à la
vitesse équatoriale de la planète, inférieure à 12 m s![]() .
.
La différence principale entre les simulations de la superrotation
mentionnées plus haut et le cas de Titan provient du cycle saisonnier
découlant de la grande obliquité de Titan
(26.7![]() ):
pendant presque une demi année autour du solstice, la circulation méridienne
moyenne est dominée par une seule cellule de Hadley, s'étendant
de pôle à pôle, avec ascendance dans les latitudes estivales.
Cette circulation méridienne crée un jet circumpolaire intense,
analogue du jet-stream sur Terre.
C'est seulement près des équinoxes et en moyenne annuelle que la circulation
méridienne moyenne est composée de deux cellules symétriques comme
dans le cas des simulations idéalisées.
On revient plus en détail sur la description de la circulation méridienne
moyenne par la suite. On se contente à ce niveau d'en donner une
représentation schématique sur la Fig. 5.6.
):
pendant presque une demi année autour du solstice, la circulation méridienne
moyenne est dominée par une seule cellule de Hadley, s'étendant
de pôle à pôle, avec ascendance dans les latitudes estivales.
Cette circulation méridienne crée un jet circumpolaire intense,
analogue du jet-stream sur Terre.
C'est seulement près des équinoxes et en moyenne annuelle que la circulation
méridienne moyenne est composée de deux cellules symétriques comme
dans le cas des simulations idéalisées.
On revient plus en détail sur la description de la circulation méridienne
moyenne par la suite. On se contente à ce niveau d'en donner une
représentation schématique sur la Fig. 5.6.
Sur le graphique de gauche de la Fig. 5.7, on montre une moyenne zonale du vent zonal simulé au solstice d'hiver nord. On voit bien à la fois la superrotation d'ensemble de l'atmosphère, particulièrement importante au-dessus de 20 hPa, et le jet d'hiver très marqué vers 1 hPa. Sur le graphique de droite, on montre la comparaison entre les profils de vent zonal extraits à différents niveaux d'altitude et les résultats de l'occultation stellaire de 1989 (Hubbard, 1993). La courbe reconstituée à partir de l'occultation ne contient en fait de l'information qu'entre 0 et 60 degrés sud et les oscillations sont liées à la méthode utilisée pour la reconstitution. C'est à dire finalement qu'elle indique essentiellement un vent zonal avoisinant la centaine de mètres par seconde à l'équateur et un jet d'hiver très marqué. La simulation aux altitudes sondées par l'occultation, vers 0.25 hPa ou 250 km, en bon accord avec l'observation pour le vent équatorial, semble sous-estimer l'intensité du jet.
Comme pour les simulations idéalisées présentées plus haut, c'est la circulation méridienne moyenne qui est responsable du transport vers le haut de moment cinétique. Comme dans ces simulations aussi, ce sont les ondes planétaires qui transportent le moment cinétique vers l'équateur (Fig. 5.8), en remontant le gradient de moment cinétique, et permettent ainsi de maintenir un maximum de moment cinétique à l'équateur.
Comme dans les simulations idéalisées enfin, ces ondes planétaires sont créées par l'instabilité barotrope de l'écoulement qui apparaît notamment sur le versant équatorial du jet hivernal.
A noter que des structures similaires sont observées dans la haute atmosphère de la Terre, ou le jet hivernal présente, de part et d'autre, des régions d'instabilité barotrope associées à la présence d'ondes planétaires de grande échelle (Hartman, 1983). Sur la Fig. 5.9, on montre à la fois pour Titan et pour la Terre la structure de ce jet hivernal (en haut) et la dérivée latitudinale de la vorticité potentielle qui permet d'identifier les régions d'instabilité barotrope (en grisés).
Les simulations présentées plus haut, si elle semblent en bon accord avec les résultats des occultations, sous-estiment en revanche fortement les contrastes latitudinaux de température déduits des mesures Voyager. On montre sur la Fig. 5.10 la distribution des températures dans le plan méridien. Sur la figure de gauche, on montre des résultats obtenus en coupant la dynamique grande échelle dans le modèle. Il s'agit donc d'un calcul radiatif convectif effectué avec un cycle saisonnier. Curieusement, les contrastes latitudinaux de température qu'on obtient alors vers 1 hPa se comparent très bien avec les mesures Voyager, avec une différence d'une dizaine de degré entre 24 et 50N. De même, on observe dans cette coupe une certaine asymétrie entre le nord et le sud, et, là encore, la simulation sans dynamique colle assez bien avec l'observation avec une différence d'une dizaine de degrés entre 50S et 50N, à 1 hPa. En revanche, dans la simulation complète, avec dynamique, les contrastes sont nettement plus faibles, et s'inversent même au dessus de 1 hPa. Nous avions suggéré à l'époque que ces gradients trop faibles puissent s'expliquer par la non prise en compte, dans le calcul du transfert radiatif, des variations latitudinales de la composition atmosphérique (Hourdin et al., 1995b). On s'attend en fait de toutes façons à ce que la dynamique réduise les gradients latitudinaux de température, ce qui suggère que les contrastes obtenus sans dynamique sont eux-mêmes trop faibles (puisqu'en bon accord avec l'observation).
A la même époque, des calculs radiatifs, effectués en prenant en compte les variations de composition telles qu'elles étaient déduites des mesures Voyager, ont montré que ces variations étaient suffisantes par exemple pour expliquer l'asymétrie hémisphérique au moment de la rencontre avec Voyager (Bézard et al., 1995). Voyager avait observé notamment un contraste hémisphérique dans l'albédo visible (lié à la brume) avec une opacité plus importante de la brume dans l'hémisphère nord, et un enrichissement très marqué des différents constituants chimiques dans les hautes latitudes de l'hémisphère nord.
A la même époque également, deux études suggéraient que ces variations latitudinales des concentrations étaient en grande partie contrôlées par le transport par la circulation méridienne moyenne. Dans les deux études, un modèle bidimensionnel était développé sur la base de modèles uni-colonnes de microphysique des brumes ou de chimie en imposant un transport par une circulation de Hadley issue directement ou idéalisée à partir des résultats du modèle tridimensionnel.
Dans la première étude, en partant du modèle microphysique de McKay et al. (1989), Hutzell et al. (1995) ont montré que l'ordre de grandeur des variations saisonnières de l'albédo global de Titan, observé depuis la Terre, ainsi que l'ordre de grandeur des contrastes latitudinaux au passage de Voyager, pouvaient être expliqués par le transport par la circulation méridienne moyenne. On montre sur la Fig. 5.11 la comparaison entre les variations saisonnières observées et simulées de l'albédo. L'amplitude des variations (environ 5%) est sous-estimée par le modèle mais l'ordre de grandeur y est. On voit aussi un déphasage d'une demi saison environ. Malgré ces différences non négligeables, on voit que la dynamique est capable d'expliquer le type de variations observées.
Dans une autre étude, Lebonnois et al. (2001) ont développé sur le même principe un modèle de chimie-transport bidimensionnel en partant du code de photochimie unidimensionnel de Toublanc et al. (1995). Le transport méridien était calculé avec le schéma en volumes finis de Van Leer (1977) en utilisant une formulation analytique pour la circulation méridienne moyenne, calée sur les résultats du modèle de circulation de Titan. Une diffusion latérale était également prise en compte afin de représenter, très sommairement, le transport par les ondes planétaires.
Ce travail a permis de donner pour la première fois une explication cohérente des observations par Voyager des variations latitudinales des espèces chimiques. L'idée est la suivante. Les espèces chimiques sont créées dans la haute atmosphère par photo-dissociation de l'azote et du méthane entre 600 et 1000 km. Cette source en altitude a pour conséquence que presque toutes les espèces chimiques ont une concentration qui croit fortement avec l'altitude. Les observations Voyager concernent une région beaucoup plus basse (150-300 km) dans laquelle les molécules chimiques sont avant tout amenées depuis le haut par le transport atmosphérique. Ce transport vertical est essentiellement le fait des grandes cellules méridiennes qui produisent, durant une longue saison autour d'un solstice, une subsidence sur le pôle hivernal compensée par une ascendance dans l'autre hémisphère. La bascule entre les deux saisons se fait autour de l'équinoxe. Ce transport est responsable de la création des contrastes latitudinaux avec des concentrations plus fortes dans l'hémisphère d'hiver. Ce mécanisme est illustré sur la Fig. 5.12. Au moment du passage de Voyager, juste après l'équinoxe de printemps nord, les concentrations étaient encore maximum dans les haute latitudes de l'hémisphère nord. Sur la Fig. 5.13, on compare les variations latitudinales des concentrations des hydrocarbures et nitriles observées par Voyager avec les résultats du modèle bidimensionnel. On voit que l'ordre de grandeur des variations latitudinales est très bien restitué par le modèle. On revient beaucoup plus en détail sur cet aspect en fin de chapitre.
Pour les raisons évoquées ci-dessus, il a été décidé vers 1996 de mettre en commun les différents efforts de modélisation afin de développer un modèle de climat couplant dynamique atmosphérique, chimie et microphysique des brumes. A cause du coût numérique prohibitif du modèle tridimensionnel, et du fait du caractère relativement axi-symétrique des observations disponibles de la température et de la composition de Titan, une approche bidimensionnelle a été privilégiée. La partie dynamique de ce modèle est donc une restriction à la composante axi-symétrique de l'écoulement du modèle tridimensionnel.
Le modèle bidimensionnel est bâti sur la séparation entre
la moyenne zonale des différentes variables d'état et les perturbations
non zonales définies par rapport à cette moyenne.
Comme pour la séparation d'échelle dans le cas de la paramétrisation
des mouvements turbulents (Section 2.2), on introduit en fait une moyenne
zonale pondérée par la masse de l'air,
, où
est la moyenne zonale de ![]() .
Comme pour la séparation d'échelle aussi, l'équation de continuité
.
Comme pour la séparation d'échelle aussi, l'équation de continuité
| (5.2) |
| (5.3) |
Parce qu'on a identifié dans les simulations tridimensionnelles
(Hourdin et al., 1995b) que le transport par les ondes était essentiellement
horizontal (ou barotrope) et parce qu'on veut s'intéresser spécifiquement
au couplage entre la dynamique méridienne de grande échelle et le transport
latitudinal par les ondes, on va restreindre la paramétrisation au
transport par les perturbations de ![]() . Sous ces hypothèses, l'équation
pour
. Sous ces hypothèses, l'équation
pour ![]() peut se récrire
peut se récrire
Cette équation est valable pour les traceurs chimiques et la brume
ainsi que pour la température potentielle ou le moment cinétique
![]() .
.
![]() comprend les termes de production/destruction
chimiques ou microphysiques pour les espèces gazeuses et les brumes,
le chauffage radiatif pour la température potentielle et
le mélange vertical turbulent pour toutes les variables.
comprend les termes de production/destruction
chimiques ou microphysiques pour les espèces gazeuses et les brumes,
le chauffage radiatif pour la température potentielle et
le mélange vertical turbulent pour toutes les variables.
Afin de développer une paramétrisation physique du transport latitudinal par les perturbations non zonales, David Luz a mené une étude détaillée du transport latitudinal par les ondes planétaires avec un modèle global à une couche basé sur les équations de Saint Venant ou équations de l'eau peu profonde. En pratique, le modèle utilisé est une restriction à une couche de la partie dynamique du modèle de circulation générale tridimensionnel. Le modèle dépend d'une seule variable thermodynamique (la hauteur de la couche de fluide pour un fluide incompressible).
L'idée est d'utiliser ce modèle, avec des paramètres typiques de la stratosphère de Titan, pour étudier le développement des ondes et les propriétés de mélange associées, en relation avec l'instabilité de l'écoulement moyen. En pratique, on force le modèle en rappelant le champ de vent zonal vers un profil proche du profil observé (par occultation par exemple) ou simulé (avec le modèle de circulation tridimensionnel), en faisant en sorte que ce profil présente des régions d'instabilité sur le versant équatorial des jets. Dans l'étude de Luz (2003), différents profils sont utilisés avec différentes constantes de temps pour le rappel.
On présente ici, sur la
Fig. 5.14 des résultats issus d'une des simulations.
On montre sur la figure le vent zonal (a) ainsi que le moment
cinétique (b) et la vorticité potentielle (c) associés.
Les courbes pleines correspondent aux profils de rappel.
La vorticité potentielle associée (c) montre clairement
les régions d'instabilité barotrope entre 30 et 50 degrés dans les deux
hémisphères.
Dans le cas présenté ici, le profil de relaxation ne comprend pas en
revanche de région d'instabilité inertielle, avec un moment cinétique
qui décroît de part et d'autre de l'équateur.
Le modèle en eau peu profonde développe des ondes qui ont pour effet de
réduire l'instabilité.
Les moyenne zonales des différents champs, une fois établi un état de régime,
sont montrées en pointillés.
Le transport de moment cinétique associé aux ondes (
![]() ,
d) est dirigé vers l'équateur (en remontant le gradient
de moment cinétique) dans les régions d'instabilité.
Ce transport tend à réduire l'intensité des jets.
Dans ces simulations, la constante de temps de rappel est fixée
à 5 jours de Titan de façon à reproduire l'ordre de grandeur du transport
latitudinal de moment cinétique obtenu avec le modèle tridimensionnel.
,
d) est dirigé vers l'équateur (en remontant le gradient
de moment cinétique) dans les régions d'instabilité.
Ce transport tend à réduire l'intensité des jets.
Dans ces simulations, la constante de temps de rappel est fixée
à 5 jours de Titan de façon à reproduire l'ordre de grandeur du transport
latitudinal de moment cinétique obtenu avec le modèle tridimensionnel.
La Fig. 5.15 montre, pour cette simulation particulière, un exemple de carte instantanée de la perturbation du vent par rapport à l'écoulement moyen. On voit que, comme dans le modèle tridimensionnel, on a à faire à des nombres d'onde petits (1 ou 2). Quand on regarde l'évolution sur le long terme de l'activité ondulatoire (graphique de droite) on se rend compte qu'après un certain temps, une dissymétrie s'installe entre les deux hémisphères (la Fig. 5.14 correspond à des moyennes entre les jours 6 et 30, avant que la dissymétrie ne s'installe). Ce comportement, constaté dans un grand nombre de simulations tests, ne semble pas lié à une erreur informatique dans le modèle. On a par exemple vérifié, après une bascule nord/sud de tous les champs du modèle à un instant donné, que l'activité la plus forte se maintenait bien dans l'hémisphère opposé de celui où elle était avant la bascule. Ce type de comportement avait en fait déjà été observé dans des simulations effectuées pour étudier les ondes dans l'atmosphère de Vénus (Rossow, 1983). Une certaine asymétrie entre les deux jets est également rapportée pour les observations de vent vénusiens par suivi de nuages dans l'UV par Rossow et al. (1990), alors même que le forçage saisonnier est presque inexistant sur Vénus. Les auteurs concluaient à l'époque de cette étude sur la possibilité d'un comportement asymétrique de la dynamique des atmosphères de planètes en rotation lente. Ce point n'a pas pu être étudié davantage mais le modèle et les simulations sont toujours là.
|
On a ensuite regardé l'impact de ces ondes sur le transport latitudinal
des espèces traces. Là encore, on a utilisé différents profils et constantes
de temps de rappel pour évaluer le transport latitudinal par les ondes.
On montre par exemple, sur la Fig. 5.16, des simulations dans
lesquelles on injecte un traceur dans une bande de latitude et on rappelle
en permanence le champ de traceur vers cette concentration initiale
avec une constante de temps de 5 jours de Titan.
Les graphiques du haut montrent la distribution initiale et les graphiques
du bas une distribution instantanée après qu'un état de régime s'est
établi. Alors que l'énergie cinétique des perturbations est maximale
dans les hautes latitudes (Fig. 5.15), le traceur émis entre 60 et
N n'est
presque pas affecté par le transport, autrement que par une déformation
de la bande de traceur.
Le mélange latitudinal est en fait important uniquement dans la région
d'instabilité, entre 20 et
de latitude.
Dans cette région, on retrouve une figure classique, dite
en ![]() il de chat, décrite pour la première fois par
Kelvin (1880).
il de chat, décrite pour la première fois par
Kelvin (1880).
Le modèle prédit donc un mélange très intense sur le versant équatorial du jet hivernal, et une relative isolation du vortex polaire. Ce comportement explique en fait en partie la brusque rupture de pente observée dans les données Voyager aux abords du vortex polaire nord, mal prise en compte dans les premières simulations de la composition chimique (Fig. 5.13) dans lesquelles le mélange latitudinal était calculé avec une diffusion turbulente ne dépendant pas de la latitude.
Ce travail a ensuite été utilisé pour dériver une paramétrisation plus physique de ces ondes transitoires pour le modèle climatique latitude-altitude.
Pour paramétriser le transport latitudinal de traceurs par les
ondes, on utilise une approche en longueur de mélange, pour laquelle
le flux latitudinal de traceur s'écrit
Les simulations en eau peu profonde sont utilisées directement pour estimer le coefficient de diffusion à partir du rapport entre le flux latitudinal et le gradient de traceur. Un exemple d'un tel calcul est montré sur la Fig. 5.17 pour un traceur relaxé vers un profil sinusoïdal. Comme pour les traceurs émis dans des bandes de latitudes, on retrouve que le mélange est maximum dans la région de l'instabilité (à gauche) ce qui se traduit par un coefficient de diffusion maximum dans cette région (courbe pleine, à droite). Des tests ont montré que la forme de ce coefficient était peu sensible au choix du profil de relaxation pour le traceur.
Pour la paramétrisation, on choisit de représenter ce pic par une
fonction de Cauchy
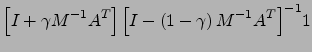 est l'amplitude,
est l'amplitude,
Le dernier pas consiste à relier les paramètres
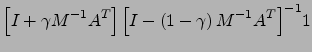 ,
, ![]() et à l'écoulement moyen (fermeture).
Pour l'amplitude, ceci peut être fait au moyen d'un paramètre
mesurant le degré de l'instabilité.
Des tests systématiques, effectués avec différentes constantes de relaxation
pour le champ de vent - permettant d'obtenir des instabilités plus ou
moins fortes - ont montré que
l'intégrale du gradient de vorticité potentielle dans sa
partie négative
et à l'écoulement moyen (fermeture).
Pour l'amplitude, ceci peut être fait au moyen d'un paramètre
mesurant le degré de l'instabilité.
Des tests systématiques, effectués avec différentes constantes de relaxation
pour le champ de vent - permettant d'obtenir des instabilités plus ou
moins fortes - ont montré que
l'intégrale du gradient de vorticité potentielle dans sa
partie négative
| (5.7) | |||
| (5.8) |
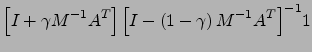 .
La relation entre intensité de l'instabilité
.
La relation entre intensité de l'instabilité 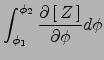 et
et 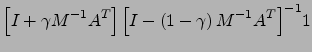 est ajustée à
partir des simulations en eau peu profonde. La formule
est ajustée à
partir des simulations en eau peu profonde. La formule
|
Le transport latitudinal de moment cinétique par les ondes s'effectuant
essentiellement en remontant le gradient dans la région d'instabilité,
il n'est pas possible de le représenter comme une paramétrisation en
diffusion du moment cinétique.
En revanche, ce transport aboutit à un mélange de vorticité qui tend à
ramener le profil moyen à la neutralité vis-à-vis de l'instabilité
barotrope (voir aussi Del Genio et al., 1993; Allison et al., 1994).
A partir de ces remarques, on choisit une paramétrisation du transport
de moment cinétique basée sur une approximation du mélange de la vorticité.
Si on l'applique à la vorticité relative (le résultat est le même pour
la vorticité absolue)
On peut obtenir l'Eq. 5.11 en prenant, pour décrire l'effet des ondes
sur le vent zonal, l'opérateur
La paramétrisation ne dépend plus alors que de la constante de temps
![]() qu'on relie au degré d'instabilité
de l'écoulement dans la couche du modèle considéré
(cette constante ne dépend plus ici que de l'altitude)
avec une formule de la forme
qu'on relie au degré d'instabilité
de l'écoulement dans la couche du modèle considéré
(cette constante ne dépend plus ici que de l'altitude)
avec une formule de la forme
Sur la Fig. 5.18, on présente un test numérique des nouvelles paramétrisations. On effectue la validation pour un modèle unidimensionnel, en latitude, version axi-symétrique du modèle global en eau peu profonde. 5.2Dans ce modèle, l'ensemble des équations se résume aux termes de relaxation (sur le vent ou les traceurs) et aux termes de transport par les ondes représentés par les paramétrisations. La Fig. 5.18 montre, pour le vent zonal (en haut), la vorticité potentielle (au milieu) et la concentration d'un traceur sinusoïdal (en bas) les profils de relaxation (croix), les résultats du modèle en eau peu profonde en état de régime (courbes pleines) et les résultats du modèle unidimensionnel avec paramétrisation (pointillés). On remarque d'abord, pour les simulations en eau peu profonde, la dissymétrie entre les deux hémisphère, le jet nord étant nettement plus affecté par le transport que son homologue austral. La paramétrisation prédit relativement bien la réduction de l'instabilité dans l'hémisphère nord mais la surestime dans l'hémisphère sud. La diffusion du champ de traceur dans la région d'instabilité est relativement bien représentée dans les deux hémisphère. A noter qu'on teste plus que l'ajustement des coefficients de mélange présenté plus haut puisque ces coefficients sont calculés ici en fonction de l'instabilité déduite de l'équilibre entre relaxation du champ de vent et mélange latitudinal paramétrisé.
Le modèle microphysique de la brume (Cabane et al., 1992) a été introduit
dans le modèle de climat en se basant sur une discrétisation de la
distribution en taille des particules.
On utilise 10 classes de rayons (contre 45 dans le modèle unidimensionnel
d'origine). La plus petite taille correspond aux macro-molécules
fraîchement créées par polymérisation avec un rayon
![]() .
La production de ces particules est pour l'instant imposée comme une
fonction de l'altitude uniquement. Dans les simulations présentées ci-dessous,
cette production a lieu dans une couche épaisse de 40 km, vers 450 km
d'altitude.
Les rayons pour les autres classes sont donnés par
.
La production de ces particules est pour l'instant imposée comme une
fonction de l'altitude uniquement. Dans les simulations présentées ci-dessous,
cette production a lieu dans une couche épaisse de 40 km, vers 450 km
d'altitude.
Les rayons pour les autres classes sont donnés par
![]() .
Le rayon des monomères est
.
Le rayon des monomères est
![]() et le rapport entre les
volumes des particules dans deux classes adjacentes est de 16.
Les particules plus grosses que
et le rapport entre les
volumes des particules dans deux classes adjacentes est de 16.
Les particules plus grosses que ![]() sont représentées comme des agrégats
fractals de dimension 2.
Le code radiatif a été modifié pour tenir compte de cette nouvelle
description des aérosols (traités comme des particules sphériques
dans le code original de McKay et al., 1989) et de leur variation latitudinale
(se reporter à Rannou, 2004, pour les détails).
sont représentées comme des agrégats
fractals de dimension 2.
Le code radiatif a été modifié pour tenir compte de cette nouvelle
description des aérosols (traités comme des particules sphériques
dans le code original de McKay et al., 1989) et de leur variation latitudinale
(se reporter à Rannou, 2004, pour les détails).
La composition chimique est calculée en utilisant un code chimique très proche de celui décrit par Lebonnois et al. (2001), à ceci près qu'il est cette fois-ci intégré directement au modèle de circulation. La composition chimique prédite par le modèle est qualitativement comparable à celle obtenue par Lebonnois et al. (2001) et est globalement en bon accord avec les observations, comme on peut le voir sur la Fig. 5.19. Les contrastes latitudinaux entre 30N et 60N sont mieux représentés que dans l'étude précédente. Comme dans l'étude de Lebonnois et al. (2001) également, les niveaux moyens des concentrations sont en général moins bien prédits que les variations latitudinales.
On utilise également dans le modèle couplé une chimie linéarisée.
Dans ce cas, la production et la perte chimique sont calculées
au moyen d'un terme de rappel vers un profil de référence avec une constante
de temps imposée, les deux étant issues de calculs préalables effectués
avec la version unidimensionnelle du modèle de chimie.
L'avantage de cette chimie linéarisée est double : 1) on évite la lourdeur
du code chimique complet - avec 44 espèces et 250 réactions -
et 2) on peut ajuster le profil de rappel de façon à avoir un meilleur accord
avec l'observation pour les concentrations stratosphériques. Ceci
est important quand on veut inclure l'effet radiatif des variations
latitudinales de la composition dans le modèle dynamique.
La chimie linéarisée n'est utilisée que pour les espèces radiativement
actives, à savoir C![]() H
H![]() , C
, C![]() H
H![]() et HCN.
Pour ces trois espèces, les résultats ``ajustés" sont comparés sur la
Fig. 5.19 aux résultats de la chimie complète ainsi qu'aux observations
Voyager.
et HCN.
Pour ces trois espèces, les résultats ``ajustés" sont comparés sur la
Fig. 5.19 aux résultats de la chimie complète ainsi qu'aux observations
Voyager.
Quand on utilise la chimie complète, une condition à la limite supérieure doit être imposée pour toutes les espèces. On a déjà dit plus haut que la chimie qui a lieu au-delà du toit du modèle de circulation a un rôle crucial pour la plupart des espèces, produites dans la mésosphère ou dans la haute stratosphère et advectées ensuite vers la stratosphère moyenne. Pour les simulations présentées ici, c'est un flux du constituant qui est prédit au sommet du modèle. Les flux pour les différentes espèces sont calculés en utilisant le modèle unidimensionnel en conditions équatoriales (voir Lebonnois et al., 2002,2003a). Faute d'information suffisante ou de modélisation appropriée, ce flux est pour le moment constant et ne dépend ni de la latitude ni de la saison. Une seconde option consistant à fixer la concentration dans la couche supérieure du modèle a été testée. Elle donne des résultats comparables à ceux présentés ci-dessous.
Pour la chimie linéarisée, la condition au sommet est traitée différemment : la concentration est contrainte à rester proche du profil de rappel en imposant dans les trois couches les plus hautes du modèle des constantes de temps arbitrairement courtes (1 jour de Titan dans la plus haute, 10 dans la suivante et 100 jours dans la troisième). Dans tous les cas, et comme on le verra par la suite, cette condition à la limite supérieure conditionne la valeur moyenne de la concentration dans la stratosphère sans modifier la distribution relative dans le plan méridien. C'est cette concentration à la limite supérieure qui est utilisée pour ajuster les concentrations du modèle avec chimie linéarisée.
La condensation des espèces chimiques est calculée en retirant de l'atmosphère tout excédant par rapport à la concentration à saturation. Cette concentration à saturation est calculée une fois pour toute, en début de simulation, en se basant sur un profil de référence de l'atmosphère (Lellouch et al., 1989). Cette approche permet d'éviter des erreurs potentielles consécutives à des erreurs sur la température simulée et de simplifier l'analyse des couplages entre dynamique et composition.
Dans les simulations présentées ci-dessous, la discrétisation est basée sur 48 bandes de latitudes d'égale largeur réparties entre les deux pôles et 55 niveaux sur la verticale, dont les 3 derniers servent de couche absorbante pour réduire la possible réflexion des ondes au sommet du modèle. Le niveau 52 se situe approximativement à 480 km. La résolution verticale est d'environ 3 km dans la troposphère, 5 km à la tropopause et 10-15 km dans la stratosphère, ce qui correspond à la moitié ou au tiers de la hauteur d'échelle. Les équations primitives sont intégrées avec un pas de temps de 3 minutes et le transfert radiatif est calculé 10 fois par jour. Des informations complémentaires sont données par Luz (2003b) et Rannou (2004).
Toutes les simulations présentées ici ont été démarrées à partir d'états initiaux hérités de simulations précédentes. Le modèle est à chaque fois intégré pendant plusieurs années (de Titan soit plusieurs siècles) jusqu'à ce que les résultats soient reproductibles d'une année sur l'autre. Il se trouve en fait que les constantes de temps mises en jeu dans la stratosphère sont beaucoup plus courtes que ce que peuvent laisser penser les constantes de temps chimiques par exemple. Les résultats montrés dans la partie sur l'enrichissement polaire correspondent par exemple à l'année 6 de la simulation, ce qui s'avère amplement suffisant.
B et C : Vue globale et détail d'une photo prise par Cassini le 24 octobre 2004 avec un filtre dans l'UV proche à une distance d'un million de kilomètres. Le Soleil illumine principalement l'hémisphère sud à cette époque de l'année. On devine le terminateur jour-nuit dans la partie haut de l'image. La brume au pôle nord est illuminée par le Soleil parce qu'elle est suffisamment haute mais la surface de la planète est dans la nuit à cet endroit (Source : NASA/JPL/Space Science Institute). D : Distribution dans le plan méridien de l'extinction de la brume simulée. La coupe montre l'extinction normalisée ( |
Une diffusion lambertienne (
Les observations montrent un hémisphère sud 25% plus réfléchissant
que le nord. Le modèle reproduit bien ce contraste nord-sud à l'époque de
Voyager ( |
Les premiers résultats obtenus avec le modèle couplé dynamique/microphysique des brumes ont permis à la fois d'expliquer l'existence des deux couches de brumes observées par Voyager (brume principale et brume détachée) et de mettre en évidence une accumulation de brume dans les hautes latitudes, conduisant à une intensification importante de la dynamique atmosphérique.
On impose que
les aérosols soient produits dans le modèle à 450 km d'altitude, dans
une zone d'une quarantaine de km d'épaisseur.
Les petits aérosols, formés par polymérisation des espèces chimiques,
sont soufflés vers le pôle d'hiver - entraînés
dans la branche haute d'une cellule de Hadley globale -
avant de pouvoir sédimenter.
A ce niveau, le vent méridien est typiquement de 2 m s![]() . Le
temps nécessaire pour se déplacer d'un rayon de Titan
. Le
temps nécessaire pour se déplacer d'un rayon de Titan ![]() , soit
, soit
![]() s, est 3 fois plus court que le temps qu'il faut aux
particules pour chuter d'une hauteur d'échelle (
s, est 3 fois plus court que le temps qu'il faut aux
particules pour chuter d'une hauteur d'échelle (
![]() s
pour une vitesse de sédimentation n'excédant pas 10 mm s
s
pour une vitesse de sédimentation n'excédant pas 10 mm s![]() ).
Ces échelles de temps sont à comparer également
aux temps caractéristiques associés à la croissance des aérosols :
typiquement 10
).
Ces échelles de temps sont à comparer également
aux temps caractéristiques associés à la croissance des aérosols :
typiquement 10![]() s pour atteindre la taille d'un monomère (Rannou et al., 1993).
Les particules, entraînées vers le pôle le long de trajectoires
relativement horizontales, sédimentent et coagulent dans les régions polaires
pour être redistribués plus bas sur l'ensemble de la planète, notamment
après le renversement de la cellule méridienne. Au moment de cette bascule,
la couche détachée disparaît momentanément pour se reconstruire ensuite
avec une subsidence sur l'autre pôle.
Entre la zone de formation et cette zone inférieure mieux mélangée,
le modèle prédit une concentration moindre des aérosols (Fig. 5.20D).
Ceci vient donner pour la première fois une explication de l'organisation
de la brume en deux couches (couche principale et couche détachée).
Cette structure en deux couches,
mise en évidence une première fois par les missions Voyager (Fig. 5.20A)
a été confirmée lors des premiers survols par Cassini (Fig. 5.20B/C).
L'accumulation d'aérosols dans la nuit polaire stratosphérique explique
également l'assombrissement de la couche de brume dans cette région
ainsi que le contraste hémisphérique, tous deux visibles sur
les photos Voyager ou Cassini.
Le modèle permet également de bien reproduire les variations
latitudinales de l'albédo de Titan au moment du passage de Voyager
(Fig. 5.21).
s pour atteindre la taille d'un monomère (Rannou et al., 1993).
Les particules, entraînées vers le pôle le long de trajectoires
relativement horizontales, sédimentent et coagulent dans les régions polaires
pour être redistribués plus bas sur l'ensemble de la planète, notamment
après le renversement de la cellule méridienne. Au moment de cette bascule,
la couche détachée disparaît momentanément pour se reconstruire ensuite
avec une subsidence sur l'autre pôle.
Entre la zone de formation et cette zone inférieure mieux mélangée,
le modèle prédit une concentration moindre des aérosols (Fig. 5.20D).
Ceci vient donner pour la première fois une explication de l'organisation
de la brume en deux couches (couche principale et couche détachée).
Cette structure en deux couches,
mise en évidence une première fois par les missions Voyager (Fig. 5.20A)
a été confirmée lors des premiers survols par Cassini (Fig. 5.20B/C).
L'accumulation d'aérosols dans la nuit polaire stratosphérique explique
également l'assombrissement de la couche de brume dans cette région
ainsi que le contraste hémisphérique, tous deux visibles sur
les photos Voyager ou Cassini.
Le modèle permet également de bien reproduire les variations
latitudinales de l'albédo de Titan au moment du passage de Voyager
(Fig. 5.21).
L'accumulation des brumes dans les régions polaires a un impact radiatif très important (Rannou, 2004). Les brumes affectent le transfert radiatif à la fois dans le spectre solaire et dans l'infra-rouge thermique. Pour le spectre solaire, les brumes peuvent à la fois réchauffer l'atmosphère par absorption du rayonnement solaire ou la refroidir plus bas par écrantement du même rayonnement solaire. Dans l'infrarouge thermique, la stratosphère se refroidit d'abord par rayonnement vers l'espace et une augmentation de l'opactié aura tendance à refroidir davantage l'atmosphère tant qu'elle est relativement transparente et au contraire à la réchauffer plus bas, quand les profondeurs optiques dépassent l'unité. L'effet d'accumulation des brumes dans les régions polaires étant maximum en hiver, ce sont de loin les effets infrarouge qui dominent. Au-dessus de 60 km, cette accumulation se traduit par un très fort refroidissement des régions polaires dans l'hémisphère d'hiver (graphique a de la Fig. 5.22). L'accumulation des espèces chimiques dans le vortex polaire à un effet équivalent mais plus haut dans l'atmosphère (Lebonnois et al., 2003b). En dessous de 200 km, c'est l'effet de diminution du refroidissement vers l'espace à cause de l'extinction accrue qui domine.
Même en moyenne sur l'année (Fig. 5.23), le renforcement des contrastes pôle-équateur est très marqué. A nouveau, c'est l'effet de la brume qui est le plus important dans la moyenne stratosphère. Cas de figure assez exceptionnel, le forçage radiatif correspondant aux variations en latitude de la brume est finalement du même ordre de grandeur que le forçage lié aux variations latitudinales et saisonnières de l'ensoleillement (Rannou, 2004). La prise en compte de ce couplage, en renforçant les gradients pôle-équateur de température, renforce également le jet des moyennes latitudes conduisant à un bien meilleur accord avec les observations aussi bien pour les températures observées par Voyager (Flasar et al., 1981) que pour les vents reconstitués à partir de l'occultation stellaire (Hubbard, 1993), comme on le voit sur la Fig. 5.24. On montre plus loin que le renforcement de la circulation méridienne associé à ce renforcement du forçage thermique de la circulation contribue aussi à améliorer la représentation des variations latitudinales des espèces chimiques.
On remarque aussi que la simulation couplée prédit une asymétrie nord/sud des températures similaire à l'obsevation par Voyager juste après l'équinoxe de printemps nord (graphique de gauche de la Fig. 5.24). L'observation de cette asymétrie avait été en son temps jugée surprenante puisque les calculs radiatifs prédisent dans la stratosphère moyenne des constantes de temps beaucoup plus courtes que la saison. Une première explication a été avancée : la nécessaire redistribution en latitude de moment cinétique au moment du changement de saison introduirait une inertie dynamique capable d'expliquer l'assymétrie observée (Flasar et Conrath, 1990). Une telle inertie n'est observée ni dans le modèle tridimensionnel ni dans le modèle bidimensionnel en l'absence de couplage avec la composition. A partir de calculs radiatifs prenant en compte les variations observées de la composition au moment de Voyager, il a été ensuite suggéré que l'asymétrie puisse provenir d'un refroidissement radiatif supérieur dans l'hémisphère nord, qui sortait de l'hiver et était encore chargé en brumes et en composés chimiques Bézard et al. (1995). Les résultats du modèle couplé plaident clairement en faveur de la seconde hypothèse. Au moins, le couplage avec la composition peut clairement à lui seul introduire une inertie dans le système climatique plus longue que les constantes de temps radiatives. Il faut cependant noter que le modèle actuel continue à prédire des températures un peu plus basses que l'observation dans l'hémisphère d'été. Des effets additionels, dynamiques, radiatifs ou autres ne sont donc pas complètement à exclure.
|
Comme on l'a dit plus haut, quasiment tous les composés chimiques observés par Voyager montrent, peu après l'équinoxe de printemps nord, un enrichissement très fort dans les latitudes polaires nord. Si on définit cet enrichissement comme le rapport entre la concentration moyenne à 50-70N et celle à 0-30N, cet enrichissement varie entre 1.4 et 20 suivant les espèces.
Dans un article de revue dans lequel il considérait la composition d'un
point de vue météorologique, Flasar (1998) avait envisagé déjà que
la subsidence, dans la stratosphère, d'espèces créées
plus haut puisse expliquer cet enrichissement.
Avec un vent méridien estimé à 4 m s![]() et une constante de temps dynamique de 4 années terrestre,
il avait estimé que cet effet de transport pouvait éventuellement
expliquer un enrichissement d'un facteur 2 pour HCN. Il concluait
que des facteurs additionnels, comme des circulations plus localisées,
étaient nécessaires pour expliquer les fortes valeurs observées pour
cet enrichissement.
Il discutait aussi à l'époque le fait que le vortex polaire devienne dynamiquement
et chimiquement isolé du reste de l'atmosphère. Dans une comparaison
relativement spéculative au trou d'ozone terrestre, il suggérait
que cette isolation puisse prendre fin avec le développement d'ondes
planétaires, mélangeant constituants, chaleur et vorticité
au travers de la frontière du vortex.
et une constante de temps dynamique de 4 années terrestre,
il avait estimé que cet effet de transport pouvait éventuellement
expliquer un enrichissement d'un facteur 2 pour HCN. Il concluait
que des facteurs additionnels, comme des circulations plus localisées,
étaient nécessaires pour expliquer les fortes valeurs observées pour
cet enrichissement.
Il discutait aussi à l'époque le fait que le vortex polaire devienne dynamiquement
et chimiquement isolé du reste de l'atmosphère. Dans une comparaison
relativement spéculative au trou d'ozone terrestre, il suggérait
que cette isolation puisse prendre fin avec le développement d'ondes
planétaires, mélangeant constituants, chaleur et vorticité
au travers de la frontière du vortex.
Comme on l'a déjà dit, le couplage du modèle photochimique de Toublanc et al. (1995) avec un code bidimensionnel de transport (basé sur une description de la circulation méridienne issue des résultats du modèle dynamique tridimensionnel de Hourdin et al., 1995b) a permis d'attribuer clairement cet enrichissement polaire observé au moment de Voyager à la subsidence, pendant l'hiver précédant l'observation, dans la branche polaire d'une grande cellule de Hadley trans-hémisphérique (Lebonnois et al., 2001). Sans facteur additionnel, le modèle expliquait même les très fortes valeurs de l'enrichissement observées par exemple pour HCN (Fig. 5.13).
Les variations latitudinales des concentrations obtenues avec le modèle couplé bidimensionnel (Fig. 5.19) sont encore plus proches de l'observation que celles (Fig. 5.13) obtenues dans la première étude de Lebonnois et al. (2001). Comme on le montre plus bas, cette meilleure représentation provient à la fois de la plus forte circulation méridienne, due en grande partie au couplage avec la brume, et de la paramétrisation interactive du mélange latitudinal par les ondes, qui, comme on l'a montré plus haut, prédit un mélange fort sur le flanc du jet mais une isolation du vortex polaire.
Si les contrastes sont essentiellement créés par le transport atmosphérique, reste à comprendre pourquoi certaines espèces montrent des enrichissements plus fort que d'autres. Lebonnois et al. (2001) avaient suggéré que des différences dans la chimie puissent être à l'origine des différences d'enrichissement. Une espèce avec un contraste plus marqué entre les sources en haut et les puits en bas pourrait effectivement avoir un gradient vertical plus marqué et, en conséquence, un enrichissement plus important dans les régions de subsidence.
En fait, on montre ci-dessous que, pour la plupart des espèces, la chimie ne joue qu'un rôle secondaire. Les variations latitudinales observées sont le fait de la combinaison du transport atmosphérique avec la condensation. Avec les concentrations observées par Voyager, la plupart des espèces chimiques condensent en effet à l'approche de la tropopause, entre 100 et 10 hPa (Fig. 5.25).
On montre ci-dessous qu'on peut retrouver les contrastes latitudinaux observés (ou simulés avec la chimie complète) en utilisant des traceurs idéalisés qu'on enlève complètement en dessous d'un niveau de pression pour singer l'effet de la condensation. On montre par la même occasion que le mélange latitudinal par les ondes contrôle le gradient vertical des composés chimiques.
![\includegraphics[height=8cm]{titan/FIGURES/hcnz.eps}](img1423.png)
![\includegraphics[height=8cm]{titan/FIGURES/ktrack.eps}](img1424.png)
|
L'explication de l'enrichissement polaire dans les hautes latitudes de
l'hémisphère nord est donc la suivante (illustrations sur la Fig. 5.26).
Pendant presque une demie année autour du solstice, la circulation
méridienne moyenne (graphique a, flèches)
est dominée, comme on l'a vu, par une cellule de Hadley pôle-à-pôle,
avec une branche ascendante dans l'hémisphère d'été (sud) et une
subsidence dans les hautes latitudes de l'hémisphère d'hiver (nord).
L'advection vers le bas des espèces chimiques, depuis la zone de production dans
la haute stratosphère, est responsable de l'enrichissement polaire
(également sur le graphique a pour HCN, grisés).
Cette circulation de Hadley crée également un jet circumpolaire
intense dans les moyennes latitudes de l'hémisphère nord (graphique b,
grisés).
Comme on l'a dit plus haut,
ce jet est instable sur son côté équatorial ce qui conduit au développement
d'ondes planétaires. Ces ondes, paramétrisées dans le modèle
(Luz, 2003b), sont responsables de l'érosion de ce vortex polaire.
On montre également sur le graphique b de la Fig. 5.26 (contours),
les valeurs de la diffusivité latérale ![]() issues de la paramétrisation.
issues de la paramétrisation.
![\includegraphics[width=15.cm]{titan/FIGURES/scaleh.eps}](img1425.png) |
Les mécanismes contrôlant la composition du vortex polaire sont résumés sur le schéma a de la Fig. 5.27.
On peut en fait quantifier l'importance relative des différents
processus de transport.
Pour les simulations avec la chimie linéarisée, l'évolution
de la concentration massique ![]() d'un composé chimique
est simplement donnée par
d'un composé chimique
est simplement donnée par
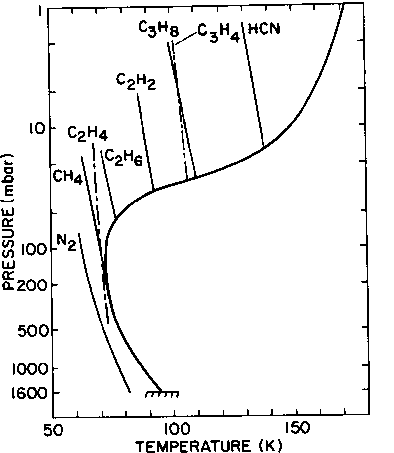 est un profil
vertical déterminé à partir de simulations photochimiques unidimensionnelles
et
est un profil
vertical déterminé à partir de simulations photochimiques unidimensionnelles
et
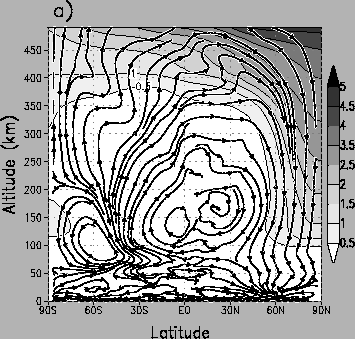 est une constante de temps déduite
des mêmes simulations (Lebonnois et al., 2001).
est une constante de temps déduite
des mêmes simulations (Lebonnois et al., 2001).
Les espèces chimiques qui descendent dans le vortex polaire depuis leur
zone de production voient leur concentration diminuer sous l'effet
combiné de l'apport d'air clair des basses latitudes par
la circulation méridienne moyenne et du mélange latéral avec
le même air clair sous l'action des ondes planétaires.
Si on note 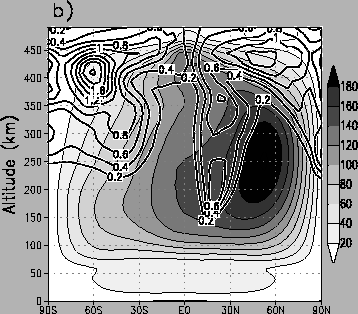 la concentration typique dans les basses latitudes,
l'``érosion'' de la concentration
la concentration typique dans les basses latitudes,
l'``érosion'' de la concentration ![]() par la diffusion latérale
(dernier terme de l'Eq. 5.15) peut être grossièrement estimée comme
par la diffusion latérale
(dernier terme de l'Eq. 5.15) peut être grossièrement estimée comme
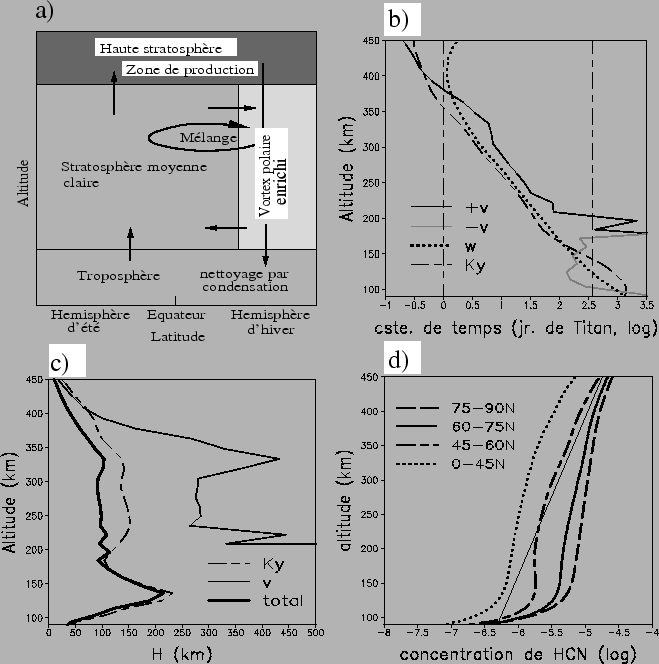 |
(5.15) |
| (5.16) |
| (5.17) |
| (5.18) |
| (5.19) |
Pour des espèces à longue durée de vie (comparée aux constantes de temps dynamiques), la forme du profil vertical de concentration est donc contrôlé par la compétition entre l'advection verticale (une advection plus rapide depuis la zone de production aura tendance à diminuer les contrastes verticaux) et un rappel vers les concentrations faibles des basses latitudes, soit par la circulation méridienne, soit par le mélange latitudinal par les ondes (qui ont tendance à renforcer les contrastes verticaux).
L'importance relative de l'advection méridienne et du mélange par les ondes
peut être quantifiée soit au travers des constantes de temps
(
![]() pour la circulation méridienne moyenne
et
pour la circulation méridienne moyenne
et
![]() pour les ondes)
soit en termes des hauteurs d'échelle associées
(
pour les ondes)
soit en termes des hauteurs d'échelle associées
(
![]() et
et
 ).
).
Sur le graphique b de la Fig. 5.27, on montre, pour l'hiver nord, les constantes de temps pour l'advection verticale et méridienne, ainsi que pour le mélange latitudinal par les ondes. L'advection méridienne domine dans la partie haute de la cellule de Hadley (au-dessus de 400 km) ainsi que dans la basse stratosphère (entre 100 et 150 km) où le vent méridien est négatif. Cette région correspond à la branche de retour de la cellule de Hadley. Les valeurs typiques des constantes de temps varient d'environ une année de Titan à 120 km jusqu'à moins d'un jour de Titan au-dessus de 1 km. Comme on le montre plus bas, ces constantes de temps sont, pour beaucoup d'espèces, nettement plus courtes que les constantes chimiques. La hauteur d'échelle dynamique (graphique c) est de l'ordre de 100 km dans la moyenne stratosphère, région dans laquelle elle résulte principalement d'une compétition entre le transport vers le bas par la circulation méridienne moyenne et le mélange latéral par les ondes.
Sur le graphique d, on montre, pour la même saison et pour différentes
gammes de latitude, les profils verticaux de HCN obtenus avec la chimie
linéarisée.
La droite sur ce graphique correspond à une hauteur d'échelle constante
de 100 km.
Cette échelle est proche des profils simulés de HCN au-dessus de
250 km entre 45 et 60N, c'est à dire aux frontières du vortex polaire,
dans la région de mélange.
Entre 100 et 150 km, la hauteur d'échelle est beaucoup plus grande
du fait d'un mélange moindre. A noter que le profil 45-60N montre
en fait un maximum local de concentration dans ces altitudes, du fait
de l'apport d'air plus riche depuis le c![]() ur du vortex.
ur du vortex.
Cette forme du profil vertical, avec trois pentes distinctes et une
région bien mélangée dans la stratosphère moyenne, entre 150 et
400 km, est en très bon accord avec des observations récentes
des composés azotés sur Titan (Marten, 2002).
Les simulations des mêmes profils verticaux effectuées avec des
modèles photochimiques unidimensionnels ont pour leur part
tendance à systématiquement surestimer les contrastes verticaux
à ces altitudes (cf. la Figure 1 dans Hidayat, 2002).
L'advection verticale par la circulation de Hadley est en fait beaucoup
plus efficace pour transporter les espèces chimiques à longue distance
que le mélange turbulent.
On peut s'en convaincre en comparant les constantes de temps diffusives
,  (où
(où ![]() est l'échelle caractéristique
des contrastes verticaux de composition et
est l'échelle caractéristique
des contrastes verticaux de composition et ![]() la diffusivité
verticale), et advective,
la diffusivité
verticale), et advective, ![]() .
Entre 250 et 150 km, la constante de temps associée à l'advection verticale
passe de 10 à 100 jours de Titan.
Il faudrait pour singer l'effet du transport vertical par la cellule
de Hadley, utiliser des diffusivités de l'ordre de 100-5000 m
.
Entre 250 et 150 km, la constante de temps associée à l'advection verticale
passe de 10 à 100 jours de Titan.
Il faudrait pour singer l'effet du transport vertical par la cellule
de Hadley, utiliser des diffusivités de l'ordre de 100-5000 m![]() s
s![]() (en considérant que
(en considérant que ![]() 200 km).
200 km).
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Les espèces chimiques qui descendent dans le vortex polaire atteignent généralement leur concentration de saturation en approchant de la tropopause, ce qui explique la décroissance rapide observée sur les profils verticaux de HCN par exemple (graphique d de la Fig. 5.27).
Pour la plupart des espèces, la concentration à saturation
au niveau de la tropopause glaciale de Titan (![]() K) est
inférieure de plusieurs ordres de grandeur aux concentrations
observées dans le vortex, dans la stratosphère moyenne.
L'air qui est recyclé par les régions polaires remonte
donc aux latitudes plus basses avec des concentrations chimiques
extrêmement faibles.
Cet air est alors petit à petit contaminé par l'air pollué
des régions polaires, soit au travers de l'advection méridienne
soit par le mélange latitudinal par les ondes.
Les contrastes latitudinaux observés par Voyager
pour des altitudes allant de 80 à 200 km sont donc essentiellement
contrôlés par cette capacité du mélange latitudinal à contaminer
l'air clair qui monte de la troposphère.
Comme on le voit sur la Fig. 5.27, c'est plutôt l'advection
méridienne qui va dominer en dessous de 150 km (courbe grise
du graphique b).
K) est
inférieure de plusieurs ordres de grandeur aux concentrations
observées dans le vortex, dans la stratosphère moyenne.
L'air qui est recyclé par les régions polaires remonte
donc aux latitudes plus basses avec des concentrations chimiques
extrêmement faibles.
Cet air est alors petit à petit contaminé par l'air pollué
des régions polaires, soit au travers de l'advection méridienne
soit par le mélange latitudinal par les ondes.
Les contrastes latitudinaux observés par Voyager
pour des altitudes allant de 80 à 200 km sont donc essentiellement
contrôlés par cette capacité du mélange latitudinal à contaminer
l'air clair qui monte de la troposphère.
Comme on le voit sur la Fig. 5.27, c'est plutôt l'advection
méridienne qui va dominer en dessous de 150 km (courbe grise
du graphique b).
Pour tester cette idée simple, nous présentons des simulations dans lesquelles les espèces chimiques sont remplacées par des traceurs idéalisés. Dans les 3 couches les plus hautes du modèle, les traceurs sont rappelés (avec les mêmes constantes de temps que pour la chimie linéarisée) vers une valeur unité. Le traceur subit le transport par la circulation méridienne et les ondes mais pas la chimie. Le traceur idéalisé est enfin complètement éliminé en dessous d'un niveau de pression donné, proche de la tropopause. Les différents traceurs idéalisés ne diffèrent les uns des autres que par le niveau de pression choisi pour les éliminer. 8 traceurs idéalisés sont considérés ici, éliminés respectivement à : 100, 80, 60, 40, 30, 20, 15 et 10 hPa.
Les traceurs idéalisés ne peuvent être comparés aux espèces chimiques simulées ou observées qu'en termes de variations latitudinales relatives. De plus, comme ces traceurs idéalisés disparaissent d'un coup à un niveau de pression donné, le niveau d'élimination retenu pour comparer à une espèce chimique donnée (dont la concentration diminue plus graduellement quand elle commence à condenser) doit être pris plus bas dans l'atmosphère, typiquement à l'altitude où la concentration de l'espèce chimique a décru d'un ordre de grandeur. Ceci se produit en général à une pression environ deux fois supérieure à celle où la condensation est initiée. Le niveau réel de condensation est estimé ici à partir de la simulation avec chimie complète, comme la pression de la couche du modèle la plus haute dans laquelle la condensation survient (à noter que ce niveau dépend donc de la concentration simulée par le modèle dans le vortex). Ce niveau de condensation ainsi que le niveau retenu pour la comparaison avec les traceurs idéalisés sont donnés pour un certain nombre d'espèce dans la Table 5.2.
Cette table donne également les valeurs de l'enrichissement polaire,
défini comme le rapport des concentrations à 50-70N et 0-30N.
On note d'abord que la comparaison entre données et simulations avec
la chimie complète fait apparaître un bon accord pour la plupart des
espèces, à l'exception de C![]() H
H![]() - dont l'enrichissement apparaît en
fait plus près du pôle que ne le suggère l'observation -,
C
- dont l'enrichissement apparaît en
fait plus près du pôle que ne le suggère l'observation -,
C![]() H
H![]() et HC
et HC![]() N - qui sont sans doute affectés par des
processus chimiques non pris en compte dans le modèle comme
la production de brumes par polymérisation -.
Pour la plupart des espèces
(C
N - qui sont sans doute affectés par des
processus chimiques non pris en compte dans le modèle comme
la production de brumes par polymérisation -.
Pour la plupart des espèces
(C![]() H
H![]() , C
, C![]() H
H![]() , C
, C![]() H
H![]() , HCN, HC
, HCN, HC![]() N),
les enrichissements obtenus avec la chimie complète et avec les traceurs idéalisés
diffèrent de moins de 50
N),
les enrichissements obtenus avec la chimie complète et avec les traceurs idéalisés
diffèrent de moins de 50![]() .
Cet accord d'ensemble montre bien que le niveau auquel les espèces sont
éliminées contrôle pour une large part l'enrichissement polaire.
Le rôle de second plan joué soit par la chimie (dans le monde réel)
soit par la spécification
des conditions à la limite supérieure (dans le monde numérique),
est détaillé ci-dessous.
.
Cet accord d'ensemble montre bien que le niveau auquel les espèces sont
éliminées contrôle pour une large part l'enrichissement polaire.
Le rôle de second plan joué soit par la chimie (dans le monde réel)
soit par la spécification
des conditions à la limite supérieure (dans le monde numérique),
est détaillé ci-dessous.
Afin d'estimer spécifiquement le rôle de la chimie pour chacune des
espèces, on peut calculer une constante de temps chimique
![]() ,
où les tendances sont calculées pour tous les termes chimiques qui détruisent
l'espèce considérée.
Les valeurs des constantes ainsi estimées sont données dans la Table 5.2.
Une seconde façon d'estimer précisément et spécifiquement le rôle de
la chimie consiste à intégrer le modèle chimique mais en annulant les
constantes de réactions.
On parlera ci-dessous de chimie nulle (se reporter à la Table 5.3).
Les valeurs obtenues pour l'enrichissement polaire avec
la chimie nulle ne se départissent pas de plus de 20% de celles
obtenues avec chimie complète, excepté pour C
,
où les tendances sont calculées pour tous les termes chimiques qui détruisent
l'espèce considérée.
Les valeurs des constantes ainsi estimées sont données dans la Table 5.2.
Une seconde façon d'estimer précisément et spécifiquement le rôle de
la chimie consiste à intégrer le modèle chimique mais en annulant les
constantes de réactions.
On parlera ci-dessous de chimie nulle (se reporter à la Table 5.3).
Les valeurs obtenues pour l'enrichissement polaire avec
la chimie nulle ne se départissent pas de plus de 20% de celles
obtenues avec chimie complète, excepté pour C![]() H
H![]() et C
et C![]() H
H![]() .
Le désaccord entre chimie nulle et complète pour C
.
Le désaccord entre chimie nulle et complète pour C![]() H
H![]() est cohérent
avec les constantes de temps relativement courtes obtenues par la première
méthode.
Pour C
est cohérent
avec les constantes de temps relativement courtes obtenues par la première
méthode.
Pour C![]() H
H![]() , le désaccord observé malgré des constantes de temps
très longues est à relier aux valeurs très faibles du flux
qu'on impose pour la chimie complète au sommet du modèle.
C'est sans doute une sous-estimation de ce flux qui explique à la fois
ce comportement de C
, le désaccord observé malgré des constantes de temps
très longues est à relier aux valeurs très faibles du flux
qu'on impose pour la chimie complète au sommet du modèle.
C'est sans doute une sous-estimation de ce flux qui explique à la fois
ce comportement de C![]() H
H![]() et la sous-estimation globale des concentrations
de cette espèce par le modèle.
et la sous-estimation globale des concentrations
de cette espèce par le modèle.
Pour les autres espèces, l'accord entre chimie nulle et traceurs idéalisés est relativement bon, au regard du traitement très différent de la condition à la limite supérieure du modèle et de la condensation (se reporter au descriptif des différentes simulations dans la Table 5.3). Cet élément plaide pour une relative robustesse des résultats présentés ci-dessus. En particulier, la façon dont on spécifie la condition au sommet, qui conditionne la concentration moyenne dans la stratosphère, ne semble pas affecter les variations latitudinales de composition.
Enfin, on voit clairement que c'est en premier lieu
le niveau de condensation qui
contrôle l'amplitude de l'enrichissement polaire.
Une condensation plus haut produira un enrichissement plus fort.
On note aussi que pour un même niveau de condensation, une observation
plus bas, donc plus proche de ce niveau de condensation, résulte
en un enrichissement observé plus fort (comparer
les résultats obtenus pour C![]() H
H![]() et CH
et CH![]() CCH).
CCH).
La combinaison du transport atmosphérique et de la condensation contrôle non seulement l'amplitude de l'enrichissement polaire mais aussi la forme du profil latitudinal. Pour illustrer ce point, on montre sur la Fig. 5.28, pour les trois espèces actives radiativement et pour les quatre traitements possibles de la chimie, les profils latitudinaux normalisés par la valeur de la concentration à l'équateur. L'accord entre ces différents profils, pour des modèles allant de la chimie complète aux traceurs idéalisés, confirme le faible rôle joué par la chimie pour ces espèces.
|
Si les contrastes latitudinaux de la composition dépendent en premier lieu du transport atmosphérique et de l'altitude du piège froid dans la basse stratosphère, qu'est-ce que l'observation de la composition peut nous apprendre en retour sur la circulation ? Ou encore, dans quelle mesure l'accord entre composition observée et simulée est-il sensible à la représentation de la circulation atmosphérique ?
Afin de répondre à ces questions, nous présentons ci-dessous une
série d'expériences de sensibilité, dans lesquelles on fait varier
artificiellement l'une des composantes de la circulation.
Un facteur multiplicatif (0,3 ou 3) est appliqué, soit simultanément
sur ![]() et
et ![]() soit sur la diffusivité
soit sur la diffusivité ![]() .
Ce facteur n'est pris en compte que pour le transport des espèces
chimiques HCN, C
.
Ce facteur n'est pris en compte que pour le transport des espèces
chimiques HCN, C![]() H
H![]() et C
et C![]() H
H![]() , représentées au moyen de la
chimie linéarisée.
, représentées au moyen de la
chimie linéarisée.
On analyse également l'effet sur la composition de la prise en compte du couplage avec la brume ou avec la chimie à partir des simulations dont on a déjà montré plus haut des résultats (Figs. 5.22 et 5.23). En pratique, le couplage avec la brume est coupé en appliquant une diffusion latitudinal très forte sur les traceurs correspondants. Dans ces simulations, la production totale de brume doit être très fortement réduite pour obtenir le même albédo géométrique de Titan que dans la simulation couplée (Rannou, 2004). En effet, la brume étant préférentiellement accumulée aux pôles dans les simulations couplées, et les régions polaires pesant faiblement dans le calcul de l'albédo planétaire, il faut plus de brumes dans une simulation couplée pour obtenir un albédo du même ordre de grandeur. Pour sa part, le couplage entre chimie et dynamique est coupé en calculant les opacités atmosphériques, non pas avec la composition chimique prédite par le modèle mais à partir de profils verticaux de référence. On utilise les résultats de Lellouch et al. (1989) pour le méthane et Coustenis et al. (1989) pour l'éthane et l'acétylène. Dans cette simulation non couplée à la chimie, les espèces chimiques sont cependant transportées normalement ce qui permet de comparer la composition à celle obtenue avec les autres simulations. Pour éviter d'avoir à analyser des rétroactions complexes, les simulations avec dynamique modifiée artificiellement sont effectuées sans couplage avec la chimie.
Sur le graphique du haut de la Fig. 5.29, on compare
aux observations Voyager (les barres d'erreur sur la figure)
l'enrichissement polaire en C![]() H
H![]() et HCN obtenu
pour les différentes configurations.
Pour la version couplée, le contraste observé est très bien reproduit pour
les deux espèces. L'enrichissement est beaucoup plus fort (respectivement
faible) si le mélange latitudinal est diminué (respectivement augmenté)
ou si l'advection moyenne est renforcée (respectivement diminuée).
L'observation de la composition apporte donc une contrainte relativement
forte sur l'intensité comparée de l'advection et du mélange latitudinal
par les ondes. Ceci fournit donc une validation supplémentaire
de cette circulation dans le modèle de climat de Titan.
et HCN obtenu
pour les différentes configurations.
Pour la version couplée, le contraste observé est très bien reproduit pour
les deux espèces. L'enrichissement est beaucoup plus fort (respectivement
faible) si le mélange latitudinal est diminué (respectivement augmenté)
ou si l'advection moyenne est renforcée (respectivement diminuée).
L'observation de la composition apporte donc une contrainte relativement
forte sur l'intensité comparée de l'advection et du mélange latitudinal
par les ondes. Ceci fournit donc une validation supplémentaire
de cette circulation dans le modèle de climat de Titan.
Le couplage avec la chimie tend en fait à dégrader légèrement l'accord avec les observations mais en restant dans les barres d'erreur.
Sans le couplage avec la brume, l'accord avec les observations
est très nettement dégradé, avec un contraste trop faible pour
HCN et trop fort pour C![]() H
H![]() .
Ce comportement différencié peut paraître contradictoire avec
l'explication dynamique proposée pour l'origine de ces contrastes.
En fait, ces différents comportements proviennent
de la différence d'altitude d'observation de ces deux espèces.
On présente en effet, sur la Fig. 5.30, des coupes méridiennes du rapport
des concentrations obtenues pour les simulations couplées
et découplées pour HCN (a) et C
.
Ce comportement différencié peut paraître contradictoire avec
l'explication dynamique proposée pour l'origine de ces contrastes.
En fait, ces différents comportements proviennent
de la différence d'altitude d'observation de ces deux espèces.
On présente en effet, sur la Fig. 5.30, des coupes méridiennes du rapport
des concentrations obtenues pour les simulations couplées
et découplées pour HCN (a) et C![]() H
H![]() (b),
à la saison du passage de Voyager.
La sensibilité est en fait très similaire pour les deux espèces,
avec une décroissance des concentrations d'environ 30% dans le
vortex polaire vers 160 km d'altitude, et une augmentation de 50% vers
100 km. Cette sensibilité peut être interprétée comme suit.
(b),
à la saison du passage de Voyager.
La sensibilité est en fait très similaire pour les deux espèces,
avec une décroissance des concentrations d'environ 30% dans le
vortex polaire vers 160 km d'altitude, et une augmentation de 50% vers
100 km. Cette sensibilité peut être interprétée comme suit.
L'effet principal du couplage avec la brume est un renforcement de la subsidence
dans les latitudes polaires, en hiver, dû au renforcement
du rayonnement thermique vers l'espace consécutif à l'accumulation de
la brume aux pôles (Rannou, 2004).
Ce renforcement de la circulation méridienne moyenne est illustré ici
sur le graphique c. Ce renforcement est responsable
de l'augmentation des concentrations dans la basse stratosphère
polaire.
Plus haut en altitude, l'intensification du jet, consécutif au renforcement
de la circulation méridienne moyenne, produit une intensification des
ondes, traduite dans le modèle par une intensification du
coefficient ![]() (graphique d).
Ce renforcement est particulièrement marqué vers 150 km et explique bien
la réduction des concentrations polaires dans cette gamme d'altitudes.
(graphique d).
Ce renforcement est particulièrement marqué vers 150 km et explique bien
la réduction des concentrations polaires dans cette gamme d'altitudes.
C![]() H
H![]() , qui est observé vers 160 km d'altitude, a donc
un enrichissement moindre dans le modèle couplé alors que c'est l'opposé
pour HCN, observé vers 100 km.
, qui est observé vers 160 km d'altitude, a donc
un enrichissement moindre dans le modèle couplé alors que c'est l'opposé
pour HCN, observé vers 100 km.
On montre également sur le second graphique de la Fig. 5.29 les contrastes de températures inter-hémisphériques (en gris) et les contrastes latitudinaux au sein de l'hémisphère d'hiver (en noir). Les quatre simulations avec advection modifiée des espèces chimiques montrent des résultats tous identiques à la simulation avec chimie découplée. Le couplage avec la brume renforce les contrastes latitudinaux et permet d'obtenir un bien meilleur accord avec les observations que si ce couplage n'est pas pris en compte. Là encore, le couplage avec la chimie détériore plutôt un peu l'accord, tout en restant pratiquement dans les barres d'erreur (estimées à la louche). Pour le vent zonal à 0,25 hPa (graphique du bas), la brume renforce l'intensité du jet par rapport au vent à l'équateur. La chimie tend à renforcer un peu le vent ce qui donne plutôt cette fois un meilleur accord avec les observations par occultation stellaire (Hubbard, 1993).
On voit donc que le couplage avec la brume améliore de façon significative l'accord avec toutes les données dont nous disposons, concernant à la fois directement l'intensité du vent zonal, et les contrastes latitudinaux de concentration ou de température. L'accord entre simulation et observation est moins sensible au couplage avec la chimie, l'essentiel des modifications se produisant plus haut dans l'atmosphère.
Nous nous sommes focalisés jusque là sur les conditions moyennes hivernales, afin de décortiquer la physique du transport et expliquer les répartitions simulées pour les constituants, ainsi que sur l'équinoxe de printemps nord en ce qui concerne la comparaison aux observations Voyager.
Sur la Fig. 5.31, nous montrons comment la distribution de HCN et la circulation associée varient au cours des saisons dans la stratosphère moyenne, entre 80 et 240 km d'altitude.
Peu après l'équinoxe d'automne, la concentration dans le vortex polaire (graphique a) s'accroît rapidement sous l'effet du transport vers le bas. A la même époque, le jet hivernal n'est pas encore en place et le contraste avec les latitudes plus basses (graphique c) croît très rapidement pour atteindre un premier maximum. L'enrichissement polaire commence alors à décroître sous l'effet combiné du mélange latitudinal par les ondes et de l'advection depuis le vortex. A l'approche de l'équinoxe de printemps nord, l'advection méridienne change de signe au-dessus de 150 km. L'air enrichi du vortex polaire est alors rapidement entraîné vers l'hémisphère opposé, ce qui explique la diminution rapide de la concentration à 50-70N au dessus de 180 km (graphique a) ainsi que le maximum observé de façon transitoire dans les basses latitudes (0-30N, graphique b) à cette saison dans la partie haute du domaine. Les concentrations élevées dans le vortex persistent nettement plus longtemps dans la partie basse, à la fois parce que les constantes de temps du transport sont plus longues et parce que le transport méridien et vertical ne change pas de sens dans les hautes latitudes.
Aux alentours de l'équinoxe d'autre part, la branche ascendante de la
cellule de Hadley passe d'un pôle à l'autre en transitant par les
régions équatoriales où elle apporte de l'air lavé de ses espèces
chimiques par la condensation.
L'advection de cet air clair explique qu'on observe une décroissance
des concentrations dans les basses latitudes (0-30N, graphique b)
en dessous de 150 km ainsi que le maximum observé pour l'enrichissement
(graphique c).
A cette saison, on peut noter également que l'intensité du mélange latitudinal
est minimum dans la basse stratosphère.
Mais, comme on l'a déjà indiqué, le mélange latitudinal n'a pas un rôle
prépondérant dans cette gamme d'altitude ce qui se voit ici en comparant
les graphiques d et e.
La constante de temps de 5 ans, qu'on peut déduire de la décroissance
du premier maximum de l'enrichissement polaire (graphique c)
correspond bien au temps qu'il faut pour se déplacer de 1000 km à une
vitesse de 5 mm s![]() , vitesse typique des vents méridiens rencontrés
dans la branche basse de la cellule de Hadley,
vers 120 km (graphique e).
, vitesse typique des vents méridiens rencontrés
dans la branche basse de la cellule de Hadley,
vers 120 km (graphique e).
Cette évolution saisonnière est illustrée également sous forme de 6 coupes successives de la structure méridienne, entre les équinoxes d'automne et de printemps de l'hémisphère nord (Fig. 5.31). Au moment des équinoxes (premier et dernier graphiques de la figure) on voit clairement l'advection vers le haut d'air clair par la branche ascendante de deux cellules de Hadley plus ou moins symétriques. A l'équinoxe d'automne (graphique a), de l'air riche de la haute stratosphère commence à descendre dans les hautes latitudes nord. La cellule globale de pôle à pôle s'établit alors (graphiques b à d), avec une ascendance au sud. Entre 80 et 200 km, une cellule secondaire apparaît dans l'hémisphère d'été. Celle-ci perdure jusqu'à l'équinoxe suivant. Cette cellule secondaire contribue clairement à maintenir un enrichissement important dans l'hémisphère d'été, dans la basse stratosphère.
A noter que cette cellule secondaire est beaucoup plus marquée dans les simulations (comme ici) où on prend en compte le couplage avec la brume.
A cause de cette cellule secondaire, l'air continue de descendre dans les
régions polaires même en été, ce qui produit de la condensation dans les
hautes latitudes. La condensation est montrée au moyen de carrés grisés
sur la Fig. 5.31 et on observe dans les simulations une condensation
analogue pour C![]() H
H![]() et C
et C![]() H
H![]() (résultats non montrés).
Cette cellule secondaire couplée à la condensation est en fait le
principal puits pour les espèces chimiques dans la basse stratosphère
en été.
Ceci pourrait expliquer qu'on observe des structures nuageuses près du
pôle d'été à la fois depuis la Terre
(Roe et al., 2002; Griffith et al., 1998,2000; Brown et al., 2002) comme sur la Fig. 5.33
et plus récemment lors du premier survol de Titan par Cassini.
Nos résultats montrent en tous cas que le fait que ces nuages soient
observés l'été n'est pas en contradiction avec l'hypothèse de nuages
d'origine stratosphérique associés à de la condensation dans de l'air
subsidant.
(résultats non montrés).
Cette cellule secondaire couplée à la condensation est en fait le
principal puits pour les espèces chimiques dans la basse stratosphère
en été.
Ceci pourrait expliquer qu'on observe des structures nuageuses près du
pôle d'été à la fois depuis la Terre
(Roe et al., 2002; Griffith et al., 1998,2000; Brown et al., 2002) comme sur la Fig. 5.33
et plus récemment lors du premier survol de Titan par Cassini.
Nos résultats montrent en tous cas que le fait que ces nuages soient
observés l'été n'est pas en contradiction avec l'hypothèse de nuages
d'origine stratosphérique associés à de la condensation dans de l'air
subsidant.
![\includegraphics[width=16cm]{lmdzt/IMGTITAN/h_titan_clouds_0704_02.eps}](img1460.png) |
|
La plupart des données dont nous disposons sur la composition et l'état dynamique de la stratosphère moyenne de Titan provient des observations Voyager.
On imagine donc le bond qui va être effectué dans notre connaissance de cette atmosphère avec les analyses des résultats de la descente de la sonde Huygens et les dizaines de survols de Cassini. La moisson a d'ailleurs déjà commencé. On montre par exemple sur la Fig. 5.34 une photo de la surface de Titan pris dans le proche infrarouge. On savait depuis une dizaine d'année, avec la découverte de fenêtres spectrales dans le proche infrarouge, que le sol de Titan était contrasté. Les premières photos montrent que la transition entre régions sombres et claires est abrupte, un peu comme un trait de côte. Les nuages du pôle sud qui, observés depuis la Terre, apparaissaient comme un point brillant, sont en fait morcelés (Figures 5.34 et 5.35).
Les informations sur la dynamique de la stratosphère moyenne devraient provenir
principalement du spectromètre infrarouge (CIRS),
mais on commence à penser que des suivis de nuages pourraient également
être possibles avec l'imagerie (ISS).
Les vents devaient également être estimés avec une précision meilleure
que 1 ms![]() pour la trajectoire de descente
d'Huygens en dessous de 160 km d'altitude
à partir de la mesure du décalage Doppler du signal
radio utilisé pour la transmission des données entre Huygens
et Cassini (expérience DWE, Bird, 2002).
Les mesures de décalage Doppler étaient malheureusement prévues sur celui
des deux canaux de transmission entre Huygens et Cassini qui n'a pas été
activé à bord de Cassini. Il existe encore un espoir de reconstituer
cette mesure à partir des enregistrements de ce signal effectués
en direct par des radiotélescopes terrestres.
L'imagerie de descente (DISR) et les mesures thermodynamiques
(HASI) viendront compléter ces informations
(Fulchignoni, 2002; Allison, 2004).
pour la trajectoire de descente
d'Huygens en dessous de 160 km d'altitude
à partir de la mesure du décalage Doppler du signal
radio utilisé pour la transmission des données entre Huygens
et Cassini (expérience DWE, Bird, 2002).
Les mesures de décalage Doppler étaient malheureusement prévues sur celui
des deux canaux de transmission entre Huygens et Cassini qui n'a pas été
activé à bord de Cassini. Il existe encore un espoir de reconstituer
cette mesure à partir des enregistrements de ce signal effectués
en direct par des radiotélescopes terrestres.
L'imagerie de descente (DISR) et les mesures thermodynamiques
(HASI) viendront compléter ces informations
(Fulchignoni, 2002; Allison, 2004).
Nous proposons ici quelques prédictions de ce que devrait observer
Cassini, en nous concentrant sur l'évolution saisonnière de grandeurs
qui ont déjà été observées, mais à une saison particulière.
Sur la Fig. 5.36, nous montrons ainsi l'évolution au cours des saisons
de l'enrichissement polaire en HCN et C![]() H
H![]() aux altitudes
où cet enrichissement était observé avec Voyager (graphique a).
On voit clairement les deux pics décrits précédemment pour HCN.
Pour C
aux altitudes
où cet enrichissement était observé avec Voyager (graphique a).
On voit clairement les deux pics décrits précédemment pour HCN.
Pour C![]() H
H![]() , en revanche, le second maximum n'est pas visible, pas parce
que les niveaux de condensation diffèrent mais plutôt à cause des
altitudes différentes auxquelles ces espèces sont observées.
On remarque aussi que l'enrichissement observé de HCN, au début de l'automne,
se produit avec un
retard de une à trois années terrestres si on compare à C
, en revanche, le second maximum n'est pas visible, pas parce
que les niveaux de condensation diffèrent mais plutôt à cause des
altitudes différentes auxquelles ces espèces sont observées.
On remarque aussi que l'enrichissement observé de HCN, au début de l'automne,
se produit avec un
retard de une à trois années terrestres si on compare à C![]() H
H![]() .
Ce déphasage est lui aussi directement lié à la différence d'altitude
d'observation (50 km plus basse pour HCN). La vitesse de subsidence qu'on
peut estimer à partir de ce déphasage, de l'ordre de 0.5-1.5 mm s
.
Ce déphasage est lui aussi directement lié à la différence d'altitude
d'observation (50 km plus basse pour HCN). La vitesse de subsidence qu'on
peut estimer à partir de ce déphasage, de l'ordre de 0.5-1.5 mm s![]() ,
est bien en accord avec les valeurs de
,
est bien en accord avec les valeurs de ![]() données dans la Fig. 5.31.
On voit ici que les observations de la composition permettent de remonter
presque directement au vent.
données dans la Fig. 5.31.
On voit ici que les observations de la composition permettent de remonter
presque directement au vent.
Sur le graphique b de la Fig. 5.36, on montre l'évolution saisonnière des vitesses zonales dans la stratosphère (250 km), à la fois au niveau du jet (40-70N) et de l'équateur. On ne sait pas encore si Cassini parviendra à observer ces vents au moyen par exemple du suivi de nuages. En revanche, ces vents sont typiquement ceux observés lors des occultations d'étoiles ou par effet Doppler depuis la Terre (Kostiuk et al., 2001). L'évolution du jet stratosphérique présente certaines similitudes avec celle de HCN, avec deux maxima et une longue saison hivernale, contrastant avec une courte saison d'été où la vitesse zonale est plus faible dans les hautes latitudes qu'à l'équateur.
L'évolution temporelle des contrastes de température à 1 hPa (190 km) est encore plus complexe. Les latitudes polaires sont généralement plus froides que l'équateur, sauf pendant une saison très courte autour du solstice d'été.
Les courbes montrées sur la Fig. 5.36 sont relatives à l'hémisphère nord, mais, à l'excentricité près de l'orbite de Saturne, la situation est symétrique pour l'hémisphère sud. La situation au moment de l'arrivée de Cassini correspond donc à l'année 2005 pour l'hémisphère nord et 2020 pour l'hémisphère sud. A partir de ces figures, Cassini est justement arrivée à une saison où le vent zonal est très faible dans l'hémisphère sud, avec des hautes latitudes au sud plus chaudes que l'équateur.
Comme on le voit sur le graphique f de la Fig. 5.31,
on devrait être également dans une période de relativement forte
activité ondulatoire.
Cette activité ondulatoire pourrait permettre de détecter des contrastes
longitudinaux de brumes ou de concentration environ 10![]() plus
faibles que les contrastes latitudinaux moyens.
De tels contrastes pourraient être vus par CIRS.
plus
faibles que les contrastes latitudinaux moyens.
De tels contrastes pourraient être vus par CIRS.
De nombreuses autres choses vont être observées par Cassini et Huygens. Une base de données, construite par Pascal Rannou à partir de résultats du modèle, a été mise a disposition de la communauté scientifique 5.3, de sorte qu'il sera possible de regarder a posteriori lesquelles des prédictions du modèle étaient justes ou erronées.
Le modèle de climat que nous avons développé pour Titan au fil des ans, le plus complet à l'heure actuelle, est en même temps plein d'incertitudes, d'approximations et de manques. Les pièces du puzzle ont été ajoutées les unes après les autres, permettant de résoudre de nouvelles énigmes, mais le caractère encore relativement frustre de certaines parties doit être gardé à l'esprit quand on analyse les résultats.
D'abord le modèle est axi-symétrique. Le traitement du transport par les ondes, s'il n'est pas totalement arbitraire puisque paramétrisé en fonction de l'instabilité de l'écoulement, est sûrement loin cependant de représenter la réalité des ondes dans toute sa complexité. Notons par exemple que l'instabilité barocline pourrait jouer un rôle dans les hautes latitudes alors qu'elle n'est pas du tout prise en compte par la paramétrisation. De même, à la fois à cause de la nature bidimensionnelle du modèle et de l'absence d'informations sur de potentiels contrastes en longitude au sol (albédo, relief, inertie thermique, ...), nous n'avons pas de forçage en longitude. Les ondes de gravité sous-maille, paramétrées dans les modèles terrestre et martien, ne sont pas prises en compte ici, une fois de plus pour un soucis de simplicité et en absence d'information suffisante sur les possibles sources. On conserve également dans le modèle de Titan l'approximation de couche mince, ce qui devient sans doute plus que suspect à 400 km d'altitude sur Titan. Cette approximation pourrait affecter notamment l'intensité globale de la superrotation. L'approximation de couche mince néglige en particulier les variations de la distance à l'axe des pôles dans le calcul du moment cinétique. Si on se dit que c'est le moment cinétique qui est bien prédit par le modèle, et qu'on le traduit en termes de vent zonal en tenant compte de cet effet, on obtient une surestimation de 10% du vent zonal, vers 300 km. Au sommet du modèle, on devrait également abandonner l'hypothèse d'équilibre thermodynamique local (typiquement au-dessus de quelques dixièmes de Pa, Yelle, 1991). Pour ce qui est de la composition, les concentrations simulées dans la stratosphère dépendent de façon cruciale de la condition à la limite supérieure, pour laquelle nous nous appuyons sur des calculs unidimensionnels du modèle photochimique sans effets saisonniers ni latitudinaux. La production de brume est découplée de la chimie dans le modèle. Certains travaux sont en cours actuellement pour essayer de prendre en compte ce couplage supplémentaire au moyen d'une paramétrisation de la polymérisation. Les changements de phase du méthane ne sont pas pris en compte alors qu'il a été montré qu'ils peuvent fortement influencer la circulation dans la troposphère (Tokano, 2001). Les marées gravitationnelles de Saturne devraient également être prises en compte (Tokano, 2002). Pour finir, nous devions faire une hypothèse quant à l'inertie thermique de la surface. Cette inertie thermique est fixée ici à une valeur faible, typique des continents terrestres. Cependant, des tests avec une inertie beaucoup plus grande, plus proche d'un océan, ne changent pas les résultats, sauf un peu près de la surface.
En dépit de ces nombreuses limitations, le modèle fournit une description relativement réaliste (aux vues des données actuellement disponibles) et cohérente de la composition et de la dynamique de la stratosphère.
La superrotation, d'abord prédite par la théorie et les modèles, a été
confirmée ensuite par l'observation. Tous les résultats disponibles indiquent
entre 200 et 250 km, des vents de l'ordre de 100-200 m s![]() , en bon
accord avec le modèle.
, en bon
accord avec le modèle.
La superrotation est clairement expliquée dans le modèle par le transport vers le haut de moment cinétique par la circulation méridienne moyenne. Cette même circulation méridienne est responsable de la création d'un jet d'ouest intense, dans les hautes latitudes hivernales. De l'instabilité de ce jet, découlent des ondes planétaires qui transportent le moment cinétique vers l'équateur, permettant ainsi de boucler le bilan de moment cinétique, suivant le processus de Gierasch-Rossow.
La circulation méridienne, couplée à la microphysique, permet également d'expliquer la présence d'une couche de brume isolée, dans la zone de formation, où les particules sont soufflées vers les pôles où elles s'accumulent et sédimentent avant d'être redistribuées plus bas sur l'ensemble de la planète. Le refroidissement infrarouge, dans la nuit polaire, contribue autant que les variations d'ensoleillement au forçage de la circulation méridienne dans la stratosphère de Titan. La prise en compte de cette composante est essentielle si on veut reproduire les gradients latitudinaux de température observés par Voyager.
L'enrichissement polaire simulé dans la stratosphère moyenne, causé par la subsidence d'air provenant des régions sources de la photochimie, dans la haute stratosphère, est également en très bon accord avec les observations. Pour la plupart des espèces, ce contraste n'a que peu à voir avec la chimie elle-même. Il est dû au contraste entre cet air enrichi dans la subsidence polaire et l'air clair montant de la basse troposphère, où la plupart des espèces condensent. L'amplitude de ce contraste est contrôlé par la compétition entre l'advection verticale qui crée le contraste, et le mélange latitudinal soit par la circulation méridienne moyenne, soit par les ondes planétaires, paramétrisées dans le modèle.
Le bon accord en ce qui concerne la composition, est une des indications
les plus directes du fait que les mécanismes dynamiques impliqués dans la
création de la superrotation (circulation méridienne moyenne et ondes
planétaires), sont bien à l'![]() uvre sur Titan. En particulier,
l'enrichissement polaire reste à l'heure actuelle la contrainte
observationnelle la plus directe sur l'existence des cellules de Hadley.
uvre sur Titan. En particulier,
l'enrichissement polaire reste à l'heure actuelle la contrainte
observationnelle la plus directe sur l'existence des cellules de Hadley.
En observant la composition, nous voyons donc que Cassini devrait nous donner beaucoup de contraintes sur la dynamique en jeu dans la stratosphère de Titan.
Cette situation présente certaines similitudes avec des études concernant les contrastes d'humidité dans la troposphère terrestre. Pour l'humidité, la source est en surface et la valeur à saturation diminue à mesure qu'on monte vers la tropopause. En absence de mélange, l'humidité spécifique d'une particule d'air est déterminée simplement par l'humidité à saturation la plus faible rencontrée le long de son histoire passée (plus ou moins le point le plus froid le long de la rétro-trajectoire). Là aussi, l'observation d'une espèce condensant (la vapeur d'eau) a été utilisée pour contraindre la dynamique atmosphérique. (e. g. Pierrehumbert, 1998).
On ne sait pas encore si Cassini réussira à suivre des nuages pour déterminer des vents. Il est clair en revanche que l'observation de la composition foisonnera d'informations directes ou indirectes sur la dynamique atmosphérique, et nous permettra de valider plus finement ce modèle que nous continuerons à développer.
On voit aussi qu'une mission plus longue que les 4 ans nominaux permettrait d'apprendre beaucoup de choses sur cette machine complexe qu'est le climat de Titan, notamment par exemple si on peut observer la bascule des saisons, juste après l'équinoxe de printemps.
Chaque chapitre étant doté de sa petite conclusion particulière, il s'agit avant tout ici d'essayer de tirer des enseignements et des lignes de convergence des différentes études d'une part et d'autre part de mentionner quelques-uns des sujets qui pourraient être développés à partir de là.
Une grande partie des résultats et développements présentés dans ce
document s'appuie sur l'équation d'advection des traceurs et
sa mise en ![]() uvre dans des modèles numériques.
uvre dans des modèles numériques.
Dans ces modèles numériques, seule une partie de l'écoulement atmosphérique est représentée explicitement. C'est le cas de la ``grande échelle" des modèles de climat, de la circulation méridienne moyenne dans le modèle bidimensionnel latitude-altitude de Titan ou des structures méso-échelles de la couche limite convective pour les simulations des grands tourbillons. Les autres composantes, à savoir le transport turbulent ou convectif dans les modèles de climat, le transport latitudinal par les ondes dans le modèle axi-symétrique de Titan ou le mélange sous-maille dans les simulations des grands tourbillons doivent être paramétrisés.
Pour la modélisation numérique du transport par la composante résolue de l'écoulement, j'ai souligné qu'il était important d'utiliser des schémas numériques dont les comportements physiques respectent certaines propriétés importantes comme la conservation de la quantité totale de traceur, une faible diffusivité, la positivité ou plus fondamentalement la non création d'extrema locaux et la non amplification des extrema existants. Ces propriétés sont importantes à la fois pour le bon comportement numérique des schémas, pour le couplage avec d'autres composantes du système (il est par exemple difficile de calculer le transfert radiatif au travers d'un constituant de concentration négative) et pour l'interprétation que l'on peut faire des résultats des simulations numériques.
Dans le cadre de la modélisation du climat, où l'on essaie de comprendre les phénomènes en jeu et de prédire leur réalisation sur d'autres planètes ou dans le cadre d'un possible changement du climat, il est important que les paramétrisations développées pour représenter les mouvements non résolus reposent sur des images physiques, comme la diffusion par des petits mouvements aléatoires ou le transport par une cellule ou par un spectre d'ascendances pour les modèles en flux de masse. Les paramétrisations développées doivent ensuite être validées et éventuellement ajustées à partir d'observations.
Une approche traditionnelle pour les modèles de circulation générale atmosphérique consistait à modifier une paramétrisation et à tester l'impact sur des simulations climatiques longues, en termes statistiques. La limitation principale de cette approche tient dans le fait que le climat simulé par le modèle relève d'un jeu subtile entre différentes paramétrisations. Dans un modèle climatique ``bien réglé", l'introduction d'une nouvelle paramétrisation commence souvent par dégrader les résultats en rompant cette harmonie. De plus, en cas de désaccord entre modèle et observation, il est souvent difficile d'attribuer la responsabilité du désaccord à telle ou telle partie du modèle.
Il est donc important de trouver un moyen de valider les dites paramétrisations de façon isolée. Une approche, largement développée au cours des dix dernières années dans la communauté dans le cadre de grands projets comme EUROCS, consiste à réaliser des simulations de ``cas tests" avec des modèles numériques résolvant explicitement les écoulements qu'on cherche à paramétriser. On peut alors, pour tester la paramétrisation, utiliser le forçage exact utilisé pour le modèle explicite. Cette approche a souvent été utilisée à partir de campagnes de terrain pour lesquelles on effectuait une simulations a méso-échelle aussi proche que possible des données observées ce qui rajoutait au système des contraintes observationnelles. On peut aussi effectuer des simulations explicites de cas plus ``académiques" ce qui permet de faire varier à loisir les valeurs des paramètres de forçage. On a illustré ici cette approche dans deux cas. C'est d'abord le modèle du thermique qui a été validé par rapport à une batterie de simulations des grands tourbillons effectuées pour toute une gamme de forçages thermiques et mécaniques de la turbulence. La bonne réponse aux variations des paramètres du forçage est sûrement un des arguments positifs les plus importants en faveur de cette nouvelle paramétrisation. C'est d'autre part la paramétrisation des ondes planétaires sur Titan pour lesquelles David Luz a effectué une batterie de simulations de référence avec un modèle des équations en eau peu profonde, forcé par un rappel vers un profil de vent.
On met en avant ici une approche intermédiaire et complémentaire
des deux autres : l'utilisation d'un modèle régionalisé et guidé
en combinaison avec des mesures continues.
Cette approche légère permet de valider le comportement du modèle
complet de façon relativement fine et en isolant des cas pour lesquels
telle ou telle paramétrisation va être davantage impliquée.
Cet outil est de plus en plus utilisé pour le développement
et la validation des paramétrisations du modèle LMDZ, notamment
autour du site d'observation de l'IPSL, le SIRTA.
La mise en ![]() uvre des simulations est automatique.6.1L'analyse peut en revanche s'avérer plus subtile car les différences entre
modèle et observations peuvent à nouveau
venir de toutes les paramétrisations du modèle
de climat ainsi que d'erreurs dans les analyses. Il faudra donc, suivant
les cas, développer des outils pour sélectionner des cas pertinents
pour le problème étudié.
uvre des simulations est automatique.6.1L'analyse peut en revanche s'avérer plus subtile car les différences entre
modèle et observations peuvent à nouveau
venir de toutes les paramétrisations du modèle
de climat ainsi que d'erreurs dans les analyses. Il faudra donc, suivant
les cas, développer des outils pour sélectionner des cas pertinents
pour le problème étudié.
Le fait de décomposer le transport entre différentes composantes est bien sûr une facilité pratique pour la simulation numérique. C'est aussi une façon de découper le problème physique en sous composantes interagissant entre elles ce qui permet d'accéder à une compréhension des processus contrôlant par exemple la distribution des constituants atmosphériques. L'analyse des simulations de Titan concernant la composition chimique de la stratosphère a été grandement facilitée par la décomposition de la modélisation entre circulation méridienne et transport latitudinal par les ondes. Ce découpage a facilité la quantification de l'importance relative de ces différentes composantes dans le contrôle notamment de l'enrichissement polaire.
L'introduction des traceurs dans les modèles de circulation est souvent motivée par l'étude de la composition de l'atmosphère, et, en particulier dans les modèles de circulation générale atmosphérique, par l'étude des couplages entre cette composition et le climat.
En retour, on apprend beaucoup sur l'écoulement à partir de l'analyse de ces traceurs qui peuvent être utilisés pour affiner notre compréhension des processus atmosphériques et valider les algorithmes de transport ou la représentation de la circulation atmosphérique. C'est particulièrement clair dans l'étude sur Titan où les contrastes latitudinaux de composition apparaissent finalement comme les meilleurs indicateurs de l'existence des grandes cellules de Hadley équateur pôle. Dans le même ordre d'idées, le rétro-transport est aussi un outil qui peut s'avérer extrêmement utile pour l'analyse des processus physiques de l'atmosphère.
Pour la validation des paramétrisations du transport turbulent ou convectif, on tombe malheureusement sur certains écueils. Comme on l'a vu ici les données sont souvent insuffisantes pour arbitrer entre deux paramétrisations, même quand les concentrations sont très sensibles à la paramétrisation du transport, comme dans les cas montrés sur la Fig. 2.19 pour la convection profonde ou la Fig. 3.39 pour la couche limite. Même avec des mesures suffisantes, reste le problème du jeu entre différentes paramétrisations ajustées entre elles ainsi que les incertitudes sur les sources et les processus physico-chimiques spécifiques de chaque espèce. Même dans le cas a priori particulièrement simple du radon, certaines incertitudes sur la répartition géographique des sources (on pense qu'elles peuvent varier d'un tiers environ régionalement) ou leur sensibilité au contenu en eau du sol sont une limitation. Une condition minimum pour une exploitation réelle des mesures de concentration semble être de disposer simultanément de mesures météorologiques.
Il faudrait sans doute aussi systématiser l'inclusion de traceurs avec des protocoles bien établis dans les simulations des grands tourbillons utilisées pour valider les paramétrisations des modèles de climat. C'est ce qu'avait commencé à faire Ayotte et al. (1996) dans leurs simulations de convection de couche limite. C'est une approche que nous comptons également promouvoir avec Jean-Yves Grandpeix et des collègues toulousains dans le cadre du volet modélisation du programme AMMA d'étude de la mousson africaine.
Les modèles de circulation générale atmosphérique ont été développés dans les années 70, principalement pour les besoins de la prévision météorologique. Depuis lors, ils se sont enrichis petit à petit pour devenir au cours des années 90 des outils essentiels de l'étude du système climatique. Les "modèles intégrés du climat" , incluant océan, biosphère et parfois chimie, sont utilisés en particulier pour étudier les évolutions futures du climat sous l'effet des perturbations induites par l'activité de l'homme. Le modèle de circulation du LMD, LMDZ, est par exemple la composante atmosphérique du modèle intégré de l'IPSL utilisé actuellement pour réaliser des simulations de la période 1850-2100 pour le prochain rapport du GIEC.
Le fait que ces modèles soient utilisés pour prédire des modifications du climat implique que les paramétrisations soient le plus possible basées sur une approche physique plutôt que sur des lois empiriques ajustées sur des observations actuelles. En outre, l'inclusion de nouvelles composantes fait peser un poids important sur le degré de réalisme du modèle atmosphérique. Le couplage avec l'océan nécessite par exemple d'avoir, en plus d'une bonne représentation de l'état de l'atmosphère, une représentation correcte des flux radiatifs (donc des nuages) et turbulents en surface. Le couplage avec la chimie nécessite qu'on soit capable de représenter correctement le transport vertical dans les colonnes convectives par exemple, etc ... Dans la plupart des cas, les paramétrisations des processus turbulents, convectifs et nuageux sont les points cruciaux.
En même temps, la mise en ![]() uvre systématique d'instruments de télédétection
passive et active (Radar et Lidar), sur des sites d'observation comme le
SIRTA ou dans l'espace, vient fournir une description de plus en plus
fine des processus
dynamiques et microphysiques de la couche limite atmosphérique et des
nuages.
uvre systématique d'instruments de télédétection
passive et active (Radar et Lidar), sur des sites d'observation comme le
SIRTA ou dans l'espace, vient fournir une description de plus en plus
fine des processus
dynamiques et microphysiques de la couche limite atmosphérique et des
nuages.
Ce double contexte a donné un nouvel élan au développement des paramétrisations au LMD. Pour la représentation de la convection nuageuse, c'est d'une part le schéma en flux de masse de Kerry Emanuel qui a été adopté pour la convection profonde. Cette paramétrisation a connu différentes améliorations significatives au LMD, concernant par exemple la description du mélange entre colonne convective et environnement (Grandpeix, 2004). Plus récemment, Jean-Yves Grandpeix et Jean-Philippe Lafore (CNRM) ont développé une paramétrisation des poches froides créées sous les descentes précipitantes orageuses, et qui jouent un rôle moteur dans l'organisation et la propagation des orages. En parallèle, nous avons développé, pour la couche limite, le modèle du thermique présenté dans le Chapitre 3.
L'enjeu pour les prochaines années est de développer un nouveau bloc de paramétrisations couche-limite/convection/nuages pour le modèle de climat du LMD. Avec ce nouveau modèle, on espère s'attaquer en particulier à l'épineuse question de la représentation du cycle diurne dans les modèles de climat. De nombreux systèmes nuageux présentent en effet des cycle diurnes marqués, souvent mal représentés dans les modèles de climat. C'est le cas par exemple de la dissipation des brumes matinales - sous l'effet du brassage vertical de l'air humide de la couche limite nocturne par les panaches thermiques de la couche limite convective - ou de l'apparition de cumulus de couche limite l'après-midi après une matinée bien ensoleillée.
![\includegraphics[width=16cm]{conclusion/FIGURES/guichard2.eps}](img1462.png) |
Avec Jean-Yves Grandpeix, nous pensons également pouvoir nous attaquer à la représentation du cycle diurne de la convection précipitante sur les continents. Alors que les orages ont leur maximum généralement en soirée ou en début de nuit sur les continents, les modèles tendent systématiquement à les prédire en phase avec le cycle diurne, en tout début d'après-midi. C'est ce qui est illustré sur la Fig. 6.1. Les courbes sur cette figures représentent la précipitation obtenue lors de simulations d'un cas de cycle diurne de la convection autour du site d'observation ARM dans les grandes plaines américaines. Dans les simulations à méso-échelle (les modèles utilisent ici des résolutions kilométriques et résolvent donc uniquement les nuages convectifs mais pas les structures de la couche limite) en accord avec les observations, le maximum du cycle diurne a lieu dans la soirée. Les versions unicolonnes des modèles de circulation générale, forcés avec les même champs que les modèles méso-échelles, produisent un cycle diurne en phase avec l'ensoleillement. Les schémas du bas présentent l'évolution des nuages associés au cours de la journée. On espère, avec le modèle du thermique, pouvoir simuler la phase de petits cumulus en début de journée et pouvoir prédire le déclenchement de la convection profonde plus tard dans la journée. La prise en compte de l'auto-entretien de la convection par les poches froides devrait permettre de retarder l'arrêt de la convection en fin de journée.
Le site instrumenté de l'IPSL (SIRTA) pour les moyennes latitudes et la campagne AMMA d'étude Multi-échelle de la mousson en Afrique de l'Ouest pour les tropiques devraient fournir des cadres particulièrement pertinents pour ce travail sur le cycle diurne des nuages continentaux.
La paramétrisation nuageuse, pour être adoptée dans le modèle de climat, devra également être capable de traiter des nuages très différents, comme les strato-cumulus des régions de subsidence sur les bords Est des océans tropicaux. La transition entre strato-cumulus et cumulus d'alizés pourrait nécessiter de sophistiquer d'avantage le schéma, en introduisant par exemple un compartiment supplémentaire de descente dans le modèle du thermique pour rendre compte de la possible importance dans l'organisation nuageuse des subsidences associées à l'instabilité d'entraînement en sommet de nuages.
Le nouveau jeu de paramétrisation, incluant un calcul pronostic de l'énergie turbulente de petite échelle, une représentation explicite des structures méso-échelles de la couche limite ainsi qu'une représentation des fronts de rafales sous les systèmes convectifs devrait également permettre de proposer des paramétrisations plus physiques, à la fois des flux thermodynamiques et des tensions de vents sur les océans (cf e. g. Redelsperger et al., 2000) et du soulèvement des poussières sur les déserts terrestres ou martiens. Là encore, AMMA devrait être un cadre privilégié d'étude. On montre pour illustration sur la Fig. 6.2 une photo très spectaculaire d'un matelas de poussière soulevé par un front de rafales sous une ligne de grains (photo prise au Mali par Françoise Guichard et Laurent Kergoat) et, sur la Fig. 6.3, une tempête de poussière régionale sur Mars.
Beaucoup d'études vont encore être menées dans le futur avec le modèle climatique de Titan ; certaines pour répondre à des questions en suspend (cf. la conclusion du Chapitre 5) et d'autres pour répondre à des questions que ne manqueront pas de soulever les résultats de la mission Cassini-Huygens. En parallèle, un modèle est en cours de développement pour Vénus, en lien avec la mission Venus-Express qui devrait partir prochainement.
La problématique que nous comptons aborder sur Vénus a beaucoup en commun avec celle développée sur Titan ces dernières années. D'abord, une des motivations sera de documenter et d'étudier dans le détail la superrotation atmosphérique. Venus-Express étant en orbite autour de la planète, on peut espérer obtenir plus d'information sur la structure thermique et dynamique de cette atmosphère que sur Titan (où l'on espère disposer quand même de quelques dizaines de survols par Cassini et des résultats de la descente de Huygens).
Avec ses 90 bars de CO2, son effet de serre exceptionnel, ses nuages d'acide sulfurique, son atmosphère en superrotation (l'atmosphère, au niveau du sommet des nuages vers 70 km, tourne 50 à 60 fois plus vite que la surface), Vénus est un objet particulièrement captivant pour qui s'intéresse à la dynamique et à la physique des atmosphères. Après une période d'exploration intensive dans les années 70 notamment, Vénus est un peu tombée dans l'oubli, cédant le pas à Mars et laissant un grand nombre de questions en suspend.
Or, à la fin des années 80, après les dernières missions dédiées à son atmosphère, les chercheurs se sont aperçus qu'on pouvait sonder du côté nuit l'atmosphère profonde de Vénus, sous le voile de nuages, à travers des fenêtres de transparence dans le proche infrarouge (une histoire qui rappelle là aussi Titan). Le survol par les missions Galileo et Cassini a permis pour la première fois de cartographier à haute résolution spatiale cette émission du côté nuit avec les spectro-imageurs NIMS et VIMS. Cette émission est en fait très variable spatialement, les régions sombres étant associées à des régions plus nuageuses.
Rien que pendant ces survols, les observations successives ont permis de déduire des vents à partir du suivi des structures nuageuses. Ces observations semblent également indiquer une variation latitudinale de la quantité de monoxyde de carbone vers 30 km d'altitude.
Venus-Express, en mettant en orbite un spectromètre (PFS) et un spectro imageur (VIRTIS) capables de cartographier l'émission dans ces fenêtres spectrales, offre donc une occasion unique de contraindre la dynamique atmosphérique et d'apporter en particulier des éléments clefs pour notre compréhension du phénomène de superrotation atmosphérique.
Comme pour Titan,
aucun élément tangible ne permet en effet d'affirmer que le mécanisme de Gierasch, responsable de la superrotation dans le modèle,
est bien à l'![]() uvre dans l'atmosphère de Vénus. L'atmosphère de Vénus est-elle dominée par de grandes cellules de Hadley ? Les ondes planétaires transportent-elles le moment cinétique vers l'équateur ? Quelle est l'importance des mélanges verticaux turbulents ou convectifs ? Autant de questions auxquelles la mission Venus-Express devrait permettre de nous apporter des éléments de réponse tout à fait nouveaux.
uvre dans l'atmosphère de Vénus. L'atmosphère de Vénus est-elle dominée par de grandes cellules de Hadley ? Les ondes planétaires transportent-elles le moment cinétique vers l'équateur ? Quelle est l'importance des mélanges verticaux turbulents ou convectifs ? Autant de questions auxquelles la mission Venus-Express devrait permettre de nous apporter des éléments de réponse tout à fait nouveaux.
Surtout, la plupart des observations disponibles jusque-là concernait la couche externe des nuages, très particulière parce que c'est celle qui bloque l'essentiel du rayonnement solaire. Grâce à Venus-Express, nous aurons donc accès à des données déterminantes pour la circulation, en dessous de cette couche ``superficielle". Le suivi des nuages du côté nuit devrait permettre de contraindre le vent zonal moyen et sa variabilité, la circulation méridienne, et, on espère aussi les ondes transitoires. Les observations de la composition vers 30 km (CO, OCS, H2O, D/H, SO2), si elles font apparaître des variations latitudinales des constituants, devraient également pouvoir être interprétées, comme pour Titan, en termes de circulation méridienne moyenne, sous réserve que soient développés des modèles de chimie transport appropriés.
J'espère aussi pouvoir revenir dans les années qui viennent sur
une version du modèle développée lors de ma thèse et rapidement
évoquée dans le chapitre sur Titan : le modèle à 19 paramètres.
Ce modèle était d'ailleurs au c![]() ur de mon projet de recherche
pour le CNRS, avant que je me laisse avaler par la modélisation terrestre
et le transport des espèces traces.
Si je n'ai pas réalisé ce programme, c'est avant tout histoire de temps
et d'arbitrage.
Mais il est vrai aussi que l'utilisation sur des planètes sans eau de
paramétrisations de la couche limite aussi peu physiques que celles
dont nous disposions à l'époque (sur une planète
sans eau, les ajustement convectifs et autres termes de contre-gradients
jouent à plein) me posait problème.
Le modèle du thermique vient donc compléter ce modèle en un modèle
cohérent et physique d'une atmosphère planétaire sans changement de phase.
ur de mon projet de recherche
pour le CNRS, avant que je me laisse avaler par la modélisation terrestre
et le transport des espèces traces.
Si je n'ai pas réalisé ce programme, c'est avant tout histoire de temps
et d'arbitrage.
Mais il est vrai aussi que l'utilisation sur des planètes sans eau de
paramétrisations de la couche limite aussi peu physiques que celles
dont nous disposions à l'époque (sur une planète
sans eau, les ajustement convectifs et autres termes de contre-gradients
jouent à plein) me posait problème.
Le modèle du thermique vient donc compléter ce modèle en un modèle
cohérent et physique d'une atmosphère planétaire sans changement de phase.
Je suis convaincu qu'un tel modèle peut s'avérer extrêmement utile, y compris dans le cadre de l'étude du changement climatique sur Terre. Il est important en effet, en parallèle de la modélisation lourde (dite intégrée) du climat terrestre - sur laquelle nous continuerons à travailler à l'IPSL - de développer des approches simplifiées qui permettent de décortiquer les mécanismes en jeu et d'avancer dans notre compréhension du système climatique. La modélisation idéalisée à 19 paramètres ainsi peut-être que la modélisation bidimensionnelle du climat (comme on l'a menée sur Titan et comme certains la développent actuellement au CNRM où à l'université de Chicago) sont des voix que je compte également explorer dans cette perspective.
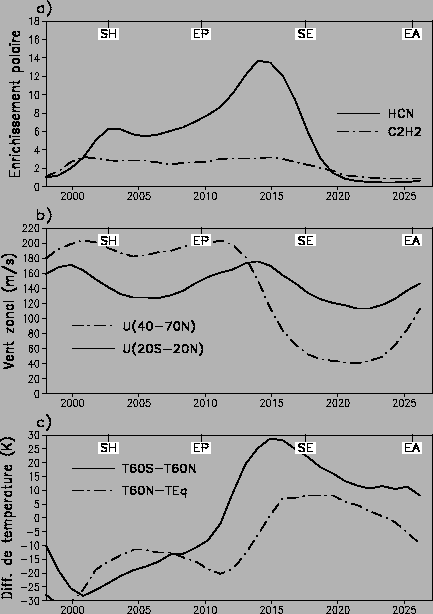 N/
N/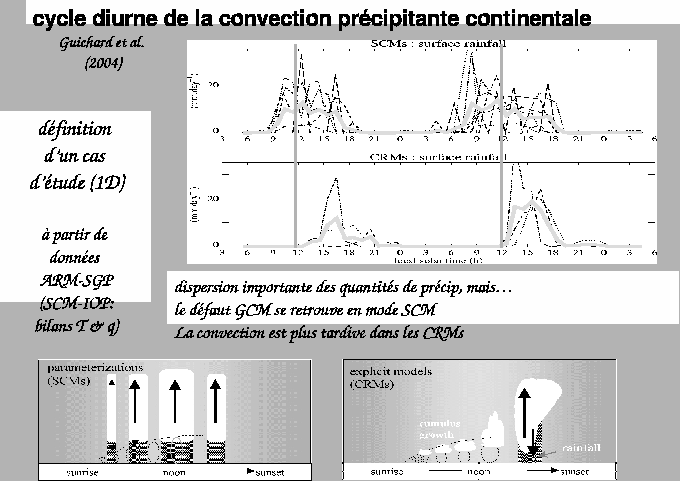 N in Its
Atmosphere, Icarus, 158, 532-544.
N in Its
Atmosphere, Icarus, 158, 532-544.
 C and O
C and O
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -white hdr
The translation was initiated by HOURDIN Frédéric on 2006-06-26
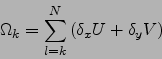 |
(2.7) |
| (2.8) |
| (2.9) |
| (2.10) |
![\begin{displaymath}
\Phi_l=\Phi_s-\sum_{k=1}^l \left[{\overline{\theta }}^{ z } \delta_z \Pi \right]_k
\end{displaymath}](img152.png) |
(2.14) |
 |
![$\displaystyle -\sum_{l=1}^Nm_l \sum_{1\le k \le l} \left[{\overline{\theta }}^{ z } \delta_z \Pi \right]_k$](img156.png) |
(2.15) | |
![$\displaystyle -\sum_{k=1}^N\sum_{k\le l \le N} \left[{\overline{\theta }}^{ z } \delta_z \Pi \right]_k m_l$](img157.png) |
(2.16) | ||
![$\displaystyle -\sum_{k=1}^N\left[{\overline{\theta }}^{ z }\delta_z \Pi \right]_k \times \frac{{\cal A}}{g} p_k$](img158.png) |
(2.17) | ||
![$\displaystyle -\frac{{\cal A}}{g}\sum_{k=1}^N\theta _k\left[{\overline{p \delta_z \Pi }}^{ z }\right]_k$](img159.png) |
(2.18) |
| (2.19) |
| (2.20) |
| (2.66) | |||
| (2.67) | |||
| (2.68) | |||
| (2.69) |
| (2.70) | |||
| (2.71) | |||
| (2.72) | |||
| (2.73) |
| (3.26) |
| (3.28) |
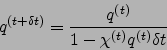 |
(3.29) |
| (3.30) |
Cette formulation numérique produit des résultats numériques presque indiscernables de l'intégration temporelle explicite de l'équation d'origine mais avec des pas de temps de typiquement quelques minutes à dizaines de minutes pour les configurations classiques du modèle de circulation.
La diffusion verticale de l'énergie cinétique turbulente est calculée a posteriori.
| HD | Heidelberg | 116 m | |
| JFJ | Jungfraujoch | 3454 m |
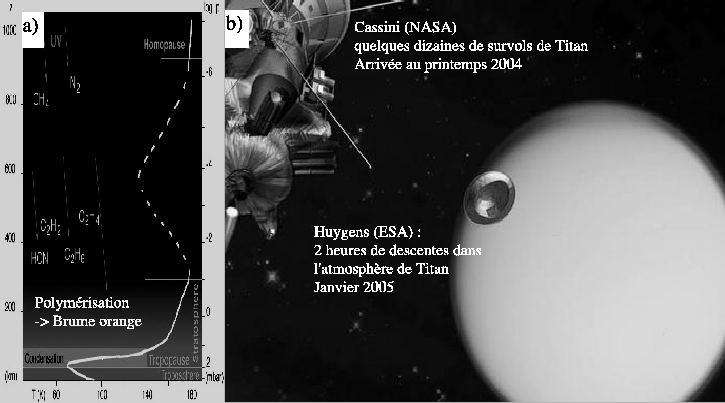 est la hauteur d'échelle de l'atmosphère,
est proche de l'altitude comptée à partir du niveau de pression
est la hauteur d'échelle de l'atmosphère,
est proche de l'altitude comptée à partir du niveau de pression