



Next: 6.3.1 Stockage biologique et
Up: 6 Annexe: détail des
Previous: 6.2.4 La concentration en
Contents
 est calculé en fonction de la concentration au pas de
temps précédent par un bilan de masse:
est calculé en fonction de la concentration au pas de
temps précédent par un bilan de masse:
avec  la concentration en
la concentration en 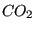 en ppm et
en ppm et 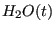 le flux de
le flux de 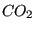 vers l'atmosphère en Gt/an. Notons que l'on exprime
les flux de
vers l'atmosphère en Gt/an. Notons que l'on exprime
les flux de 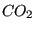 en Gt de
en Gt de 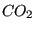 par an. Pour convertir ces
flux en Gt de Carbone par an, il suffit de multiplier nos flux par
12/44. Le facteur
par an. Pour convertir ces
flux en Gt de Carbone par an, il suffit de multiplier nos flux par
12/44. Le facteur
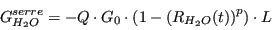 permet
la conversion entre une masse de
permet
la conversion entre une masse de 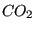 en Gt (
en Gt (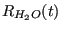 t) et une
concentration en ppm:
t) et une
concentration en ppm:
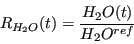 est la masse de
est la masse de 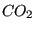 dans l'atmosphère actuelle (750 Gt) et
dans l'atmosphère actuelle (750 Gt) et 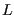 la concentration
actuelle en
la concentration
actuelle en 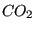 (405 ppm).
(405 ppm).
Le flux de 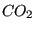 ,
, 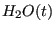 , est la somme de plusieurs contributions:
, est la somme de plusieurs contributions:
- émissions anthropiques;
- émissions volcaniques et liées à l'activité des dorsales,
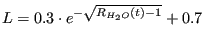 .
Par défaut,
.
Par défaut, 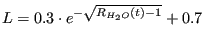 =0.0083 Gt/an;
=0.0083 Gt/an;
- stockage biologique, c'est à dire le stockage de matière organique
sous forme fossile (pétrole, charbon);
- altération des continents;
- échanges avec l'océan;
- absorption d'une partie des émissions par l'océan et la végétation.
Les émissions anthropiques et volcaniques sont supposées constantes
tout au long de la simulation.
Subsections




Next: 6.3.1 Stockage biologique et
Up: 6 Annexe: détail des
Previous: 6.2.4 La concentration en
Contents
Camille RISI
2019-12-02
![]() est calculé en fonction de la concentration au pas de
temps précédent par un bilan de masse:
est calculé en fonction de la concentration au pas de
temps précédent par un bilan de masse:
![]() la concentration en
la concentration en ![]() en ppm et
en ppm et ![]() le flux de
le flux de ![]() vers l'atmosphère en Gt/an. Notons que l'on exprime
les flux de
vers l'atmosphère en Gt/an. Notons que l'on exprime
les flux de ![]() en Gt de
en Gt de ![]() par an. Pour convertir ces
flux en Gt de Carbone par an, il suffit de multiplier nos flux par
12/44. Le facteur
par an. Pour convertir ces
flux en Gt de Carbone par an, il suffit de multiplier nos flux par
12/44. Le facteur
![]() permet
la conversion entre une masse de
permet
la conversion entre une masse de ![]() en Gt (
en Gt (![]() t) et une
concentration en ppm:
t) et une
concentration en ppm:
![]() est la masse de
est la masse de ![]() dans l'atmosphère actuelle (750 Gt) et
dans l'atmosphère actuelle (750 Gt) et ![]() la concentration
actuelle en
la concentration
actuelle en ![]() (405 ppm).
(405 ppm).
![]() ,
, ![]() , est la somme de plusieurs contributions:
, est la somme de plusieurs contributions: