Next: 2.4 Couplage du modèle Up: 2 Le modèle physique Previous: 2.2 L'intégration temporelle Contents
A l'équilibre radiatif, la puissance solaire absorbé par la Terre,
![]() , est égale à la puissance du rayonnement infra-rouge émis
par la Terre,
, est égale à la puissance du rayonnement infra-rouge émis
par la Terre, ![]() (figure 8):
(figure 8):
On définit ici les puissances ![]() et
et ![]() par unité de
surface de la Terre, en
par unité de
surface de la Terre, en ![]() .
.
![]() dépend de l'albédo planétaire:
dépend de l'albédo planétaire:
avec:
![]() l'albédo de la Terre, qui dépend notamment de la latitude des
calottes. Son calcul dans le modèle est détaillé dans la section 2.4.
l'albédo de la Terre, qui dépend notamment de la latitude des
calottes. Son calcul dans le modèle est détaillé dans la section 2.4.
![]() la puissance solaire arrivant au sommet de l'atmosphère,
en moyenne globale et annuelle. Comme à chaque instant, le soleil
n'éclaire que le quart de la surface totale de la Terre,
la puissance solaire arrivant au sommet de l'atmosphère,
en moyenne globale et annuelle. Comme à chaque instant, le soleil
n'éclaire que le quart de la surface totale de la Terre,
![]() ,
où
,
où
![]() est la constante solaire.
est la constante solaire.
![]() dépend de la température selon la loi de Stefan-Boltzmann,
modulée par l'effet de serre:
dépend de la température selon la loi de Stefan-Boltzmann,
modulée par l'effet de serre:
avec
![]() l'effet de serre: il représente la fraction de rayonnement infrarouge
émis par la Terre qui est retenue par effet de serre et ne parvient
pas à s'échapper vers l'espace.
l'effet de serre: il représente la fraction de rayonnement infrarouge
émis par la Terre qui est retenue par effet de serre et ne parvient
pas à s'échapper vers l'espace.
![]() la constante de Stefan-Boltzmann.
la constante de Stefan-Boltzmann.
Cette relation est illustrée pour différentes concentration en ![]() sur la figure 9.
sur la figure 9.
On calcule ![]() à chaque pas de temps
à chaque pas de temps ![]() , en supposant l'équilibre
radiatif:
, en supposant l'équilibre
radiatif:
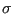
Graphiquement, ![]() correspond au point d'intersection
correspond au point d'intersection ![]() des
courbes
des
courbes ![]() et
et ![]() (figure 9).
(figure 9).
![\includegraphics[scale=0.9]{figs/debug_eqrad_fig}](img39.png)
|
La température ![]() simulée par SimClimat est basée sur le température
d'équilibre
simulée par SimClimat est basée sur le température
d'équilibre ![]() , mais avec un peu de retard pour représenter
l'effet de l'inertie thermique des océans (section 7.1).
, mais avec un peu de retard pour représenter
l'effet de l'inertie thermique des océans (section 7.1).