In the parameterization of vertical diffusion in a GCM equation 14 is discretized over the vertical and in time. In the following discussion we will assume that the calculation is performed over N levels. Variables are located at the full levels and fluxes are computed at intermediate levels, represented by dashed lines in Figure 2. Level 0 is the surface. The basic time step starts at time t when all variables are know and ends at time t+1 when all calculations are completed.
Figure 2: Levels used for the discretization of
the equations.
When equation 14 is descretized in the vertical and an implicit time-stepping is used we obtain the following finite difference formula for level l:
In order to solve this system of equations from the surface (l=0) to the top of the atmosphere or the planetary boundary (l=N) the method proposed by Richtmeyer and Morton (1967) is used. The aim is to reduce the system to a set of equation of the type:
where the coefficients 
and 
can be
computed in a descending order and then used in a back-substitution
from bottom to top which yields the profile for X at time t+1. It
is assumed here that the eddy-diffusivities 
are computed before
using atmospheric conditions at time t.
To satisfy the zero flux condition at the top in
equation 16 we have to set 
and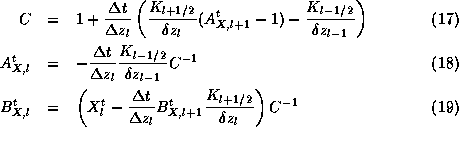 
.
This allows to start an iteration from top
to bottom which determines and over the entire
column. The following iteration formulas are obtained :
In this set of equations only 
contains information from the
surface. This implies that without any knowledge of the surface the
downward iteration can only be performed up to l=2. The back
substitution can not be performed independently from the land
surface scheme for l=1, but once 
is known
equation 16 can be solved for all 
.
In order to obtain a general interface between the land surface scheme
and the vertical diffusion scheme of the GCM a formulation has to be
derived for computing using only surface fluxes
( 
).
