The sensible and latent heat fluxes at the surface can be written in a generic form :
Depending on the type of closure chosen by the land surface scheme
the flux will be computed with variables at time t or t+1.
For surface sensible heat (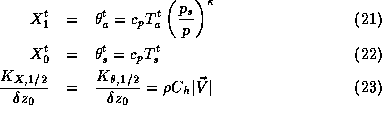 
) flux the
following correspondences are used :
where 
is the temperature at the first atmospheric level, p is
the pressure at this level, 
pressure at some reference level,
is surface temperature, 
is surface transfer coefficient
for heat and moisture (Assumed to be same here.), 
is the
density and 
is the wind speed at the first
level. Equation 20 yields evaporation (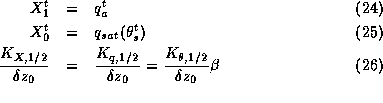 
) if the following definitions are used :
where 
is the water vapor mixing ratio at the first atmospheric level,
is the saturated humidity for the surface
temperature and 
is the aridity coefficient. is
defined as the ratio between actual and potential evaporation.
Computing these fluxes is the responsibility of the land surface
scheme and our aim is to derive an equation for 
using
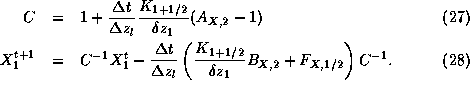as sole information from the surface. This ensures to
the land surface scheme a maximum of freedom in the choice of the
numerical scheme used for solving the surface energy balance
equation. Inserting equation 20 into
equation 15 yields :
Thus the only knowledge required for computing and
iterating equation 16 from l=2 to the top are the old
values of potential enthalpy and humidity at the lowest atmospheric
level, the surface fluxes and finally the values of 
and 
for 
obtained during the descent.
